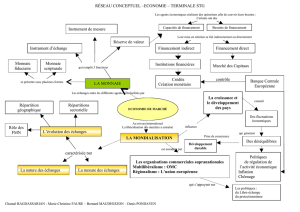
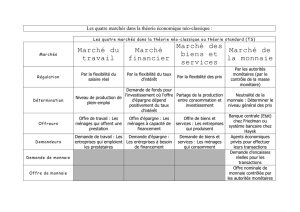
Macroéconomie essai

1
MACROÉCONOMIE
Exercices sur la théorie du revenu permanent et sur celle du cycle de vie
1. (Juin 2001) Un individu à 30 ans de l’âge de la retraite sait, avec certitude, qu’il lui reste 50
ans à vivre. Sa fortune actuelle est égale à 80.000 et il souhaite léguer un héritage de 30.000.
Chaque année, jusqu’au moment de sa retraite, il percevra un revenu égal à 8.000. Ensuite, son
revenu annuel sera de 3.000. Il cherche à répartir sa consommation au cours du temps de façon
çà maximiser le niveau de satisfaction qu’il retirera.
Calculez l’épargne annuelle de cette personne, respectivement avant et après l’âge de la retraite.
Solution
La consommation de cet individu sera la même chaque année (afin de maximiser sa
satisfaction) :
C = 80000/50 + (8000 * 30 )/50 + (3000 * 20 )/ 50 – 30000/50 = 7000
àà Epargne avant l’âge de la retraite : S = YR – C = 8000 – 7000 = 1000 épargne
àà Epargne après l’âge de la retraite : S = YD – C = 3000 – 7000 = -4000 désépargne
2. (Août 2001) Yt et Ypt représentent respectivement le revenu courant et le revenu permanent
d’un ménage à la période t.
On sait que : Ypt = Yp(t – 1) + 0,4(Yt – Yp(t – 1))
La consommation de ce ménage représente, à tout moment, 75% de son revenu permanent.
Calculez la propension marginale à consommer à court terme de ce ménage et comparez-la à sa
propension marginale à consommer à long terme.
Solution
Ypt = Yp(t–1) + 0,4(Yt – Yp(t–1))
Ct = 0,75Ypt
èè Ct = 0,75Yp(t-1) – 0,4 * 0,75Yp(t-1) + 0,75Yt
óó Ct = 0,45Yp(t-1) + 0,3Yt
èè propension marginale à consommer le revenu courant à court terme = DCt/DYt = 0,3
èè propension marginale à consommer le revenu courant à long terme : 0,75 car à long
terme le revenu permanent s’adapte au revenu courant àà g tend vers 1
On a donc : PmCCT < PmCLT
Exercices sur l’investissement (TIR, courbe d’efficacité marginale du K, …)
1. (Juin 2001) Une certaine année, une firme peut réaliser trois projets d’investissement dont le
coût est de 50.000. Elle calcule, pour chacun d’eux, le taux interne de rentabilité qui vaut
respectivement 4%, 8% et 11%.
Elle a aussi la possibilité de réaliser un quatrième projet dont le coût est également de 50.000 et
dont elle connaît la recette nette dégagée durant trois années successives :
R1 = 19.800, R2 = 14.520 et R3 = 26.620.

2
Démontrez que le taux interne de rentabilité de ce quatrième projet est égal à 10%, tracez la
courbe d’efficacité marginale du capital et calculez l’effet sur la dépense d’investissement d’une
diminution du taux d’intérêt de 8,5% à 5,5%.
Solution
Pour le 4ème projet :
Vérifions que i (TIR) est bien égal à 10% :
50.000 = 19.800/(1 + i) + 14.520/(1 + i)2 + 26.620/(1 + i)3
óó 50.000 = 19.800/(1 + 0,1) + 14.520/(1 +0,1)2 + 26.620/(1 + 0,1)3
óó 50.000 = 18.000 + 12.000 + 20.000 OK èè le TIR du 4ème projet est bien 10%
0
2
4
6
8
10
12
dépenses d'investissement (*1000)
taux d'intérêt
50
100
150
200
Pour qu’un projet soir rentable, il faut i ≥≥ r
Si r > 11% àà DI = 0
Si 10% < r ≤≤ 11% àà DI = 50.000
Si 8% < r ≤≤ 10% àà DI = 100.000
Si 4% < r ≤≤ 8% àà DI = 150.000
Si r ≤≤ 4% àà DI = 200.000
Lorsque r = 8,5% àà les projets 3 et 4 sont réalisés, la DI vaut 100.000
Lorsque r = 5,5% àà le projet 2 devient rentable et la DI passe à 150.000
Conclusion : la dépense d’investissement augmente de 50.000 lorsque le taux d’intérêt
passe de 8,5% à 5,5%.
2. (Août 2001) Une firme a, initialement, le choix entre 3 projets d’investissement dont elle
connaît le coût et le taux interne de rentabilité :
?
?
Courbe d’efficacité
marginale du capital
de la firme

3
Coût Taux interne de rentabilité
Projet 1 24.000 4%
Projet 2 47.000 13%
Projet 3 13. 000 7%
Elle a ensuite la possibilité de réaliser un quatrième projet dont le coût est de 32.000 et dont la
durée de vie est de deux années : la recette nette dégagée de ce projet la première année est
égale à 12.720 et celle obtenue la seconde année est de 22.472.
Démontrez que le taux interne de rentabilité de ce quatrième projet est égal à 6%, tracez la
courbe d’efficacité marginale du capital de la firme et dites pour quelles valeurs du taux
d’intérêt sa dépense d’investissement sera égale à 60.000.
Solution
Pour le 4ème projet :
Vérifions que i (TIR) est bien égal à 6% :
32.000 = 12.720/(1 + i) + 22.472/(1 + i)2
óó 32.000 = 12.720/(1 + 0,06) + 22.472/(1 +0,06)2
óó 32.000 = 12.000 + 20.000 OK èè le TIR du 4ème projet est bien 6%
0
2
4
6
8
10
12
14
dépenses d'investissement (*1000)
taux d'intérêt
47
60 92 116
Pour qu’un projet soir rentable, il faut i ≥≥ r
Si r > 13% àà DI = 0
Si 7% < r ≤≤ 13% àà DI = 47.000
Si 6% < r ≤≤ 7% àà DI = 60.000
Si 4% < r ≤≤ 6% àà DI = 92.000
Si r ≤≤ 4% àà DI = 116.000
?
?
Courbe
d’efficacité
marginale du
capital de la firme

4
Exercices sur la détermination du revenu national
1. (Juin 2001) Dans une économie ouverte :
C = 0,75YD – 150 Y : revenu national
I = 700 YD : revenu disponible
G = 900 C : consommation privée
X = X0 I : dépenses d’investissement
Imp = 0,15Y – 100 G : dépenses gouvernementales
T = tY – 200 X : exportations
Imp : importations
T : recettes fiscales
Le revenu national de plein-emploi est égal à 3250.
On sait qu’en augmentant les dépenses publiques de 175, on atteindrait exactement le plein-
emploi tandis que si ces dépenses diminuaient de 140, le revenu national d’équilibre vaudrait
2800.
Calculez le multiplicateur keynésien, le revenu national d’équilibre, le solde budgétaire du
gouvernement et celui de la balance des biens et services.
Solution
DG = +175 àà Y1* = Ye = 3250
DG = -140 àà Y2* = 2800
DY/DG = mult
èè (Y1* - Y0*)/(G1 - G0) = mult = (3250 – Y0*)/175 (1)
èè (Y2* - Y0*)/(G2 - G0) = mult = (2800 – Y0*)/(-140) (2)
(1) et (2) èè (3250 – Y0*)/175 = (2800 – Y0*)/(-140)
óó -140* (3250 – Y0*) = 175 * (2800 – Y0*)
èè Y0* = 3000
èè mult = -200/-140 = 10/7
Le solde budgétaire du gouvernement : S = G – T = 900 – t Y0* + 200 = 1100 – 0,4 * 3000
= -100 surplus budgétaire
Pour trouver t et X0: Y0* = 0,75(Y0* - tY0* +200) + 700 +900 +X0 – 0,15Y0* + 100 + 150
óó Y0* = 1/( 1 –0,75 * (1 – t) + 0,15) * (1700 + X0)
et 1/( 1 – 0,75* (1 – t) + 0,15) = mult = 10/7 èè 4 + 7,5t = 7 èè t = 3/7,5 = 0,4
èè Y0*= 3000 = 10/7 * (1700 + X0) èè X0 = 400
Le solde de la balance des biens et services : B = X – Imp = 400 – 0,15*3000 + 100 = 50
surplus de la balances des biens et services

5
2. (Août 2001) Une économie ouverte se caractérise par les équations de comportement
suivantes :
C = 0,8YD + 200 Y : revenu national
I = 600 YD : revenu disponible
G = 800 C : consommation privée
X = X0 I : dépenses d’investissement
Imp = 0,2Y + 100 G : dépenses gouvernementales
T = tY + 250 X : exportations
Imp : importations
T : recettes fiscales
Le revenu national de plein-emploi dans cette économie est de 3200, tandis que l’on observe un
écart déflationniste de 120. Si les dépenses publiques se réduisent de 180, le revenu national
d’équilibre, est alors, de 2700.
Calculez le multiplicateur keynésien, le revenu national d’équilibre, le solde budgétaire du
gouvernement et celui de la balance des biens et services.
Solution
Y* = Ye – ED * mult
Y0* = 3200 – 120 * mult (1)
Si DG = -180 èè Y1* = 2700
DY/DG = (Y0* - 2700)/180 = mult (2)
(1) et (2) èè Y0* = 3200 - 120 * ((Y0* - 2700)/180)
èè Y0* = 3000
èè mult = (3000 – 2700)/180 = 5/3
Pour trouver t et X0 :
Y0* = 0,8(Y0* - tY0* - 250) + 200 + 600 + 800 + X0 – 100 – 0,2 Y0*
óó Y0* = 3000 = 1/(1 – 0,8 * (1 - t) + 0,2) * (1300 + X0) èè 3000 = 5/3 * (1300 + X0) èè
X0 = 500
et 1/(1 – 0,8 * (1 - t) + 0,2) = mult = 5/3 èè 5 – 4 +4t + 1 = 3 èè t = 0,25
Le solde budgétaire du gouvernement : S = G – T = 800 - 0,25*3000 + 250 = -200
surplus budgétaire
Le solde de la balance des biens et services : B = X – Imp = 500 – 0,2*3000 - 100 = -200
déficit de la balances des biens et services