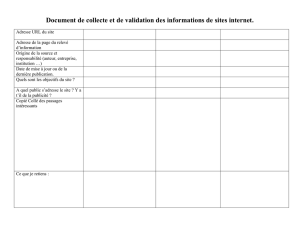
Techniques de calcul d`intégrales 54

9
Techniques de calcul d’intégrales
54
Leçon n°
Niveau Terminale S - BTS
Prérequis intégrales, accroissements finis, primitives, propriétés sur l’intégrale, trigonomé-
trie, fonction polynôme, fonction exponentielle
Références [152], [153], [154], [155], [156]
54.1 Sommes de Riemann
Soit fune application continue définie sur un segment [a, b]et à valeurs dans R,σ= (ai)1≤i≤n
est une subdivision de [a, b](c’est-à-dire a=a0< a1<··· < an=b), hest le pas de la subdivision
σ(h= max(ai+1 −ai)) et pour tout 0≤i≤n−1,ξi∈[ai, ai+1].
Définition 54.1 — Somme de Riemann. On appelle somme de Riemann associée à (f, σ, (ξi)0≤i≤n)
le réel : n−1
X
i=0
(ai+1 −ai)f(ξi).
Théorème 54.2
lim
h→0
n−1
X
i=0
(ai+1 −ai)(ξi) = Zb
a
f(x) dx.
Dv
•Démonstration — Montrons que la différence suivante peut être rendue aussi petite que
voulue :
Zb
a
f(x) dx−
n−1
X
i=0
(ai+1 −ai)f(ξi) =
n−1
X
i=0 Zai+1
ai
f(x) dx−(ai+1 −ai)f(ξi)
=
n−1
X
i=0 Zai+1
ai
(f(x)−f(ξi)).
En passant aux valeurs absolues, on a la majoration suivante :
Zb
a
f(x) dx−
n−1
X
i=0
(ai+1 −ai)f(ξi)≤
n−1
X
i=0 Zai+1
ai|f(x)−f(ξi)|dx.
Or, du théorème de Heine appliqué à fcontinue sur le segment [a, b], on déduit funiformé-
ment continue sur [a, b](et donc aussi sur chaque [ai+1, ai], c’est-à-dire :
∀E∈R∗
+,∃η∈R∗ +,∀(x, y)∈[a, b]2,(|x−y|< η ⇒ |f(x)−f(y)|< ε).

10 Leçon n°54 •Techniques de calcul d’intégrales
Pour une subdivision σde pas htel que 0< h < η, on aura :
∀x∈[ai, ai+1],|x−ξi| ≤ ai+1 −ai≤h < η.
Ce qui entraînera :
|f(x)−f(ξi)| ≤ ε.
Dans ces conditions, on peut écrire :
Zb
a
f(x) dx−
n−1
X
i=0
(ai+1 −ai)f(ξi)≤
n−1
X
i=0 Zai+1
ai
εdx=
n−1
X
i=0
ε(ai+1 −ai) = ε(b−a).
Ceci prouve bien que :
lim
h→0
n−1
X
i=0
(ai+1 −ai)f(ξi) = Zb
a
f(x) dx.
Toute intégrale est donc une limite de somme de Riemann. •
R54.3 Le résultat ci-dessus reste valable si fest continue par morceaux. Il suffit de refaire la même démonstration
avec des subdivisions adaptées à f.
Proposition 54.4 — Cas particulier d’une subdivision régulière. Pour n∈N∗, on particularise ai=
a+ib−a
net ξi=ai(donc h=b−a n). On a alors :
ai+1 −ai=b−a
n.
D’où :
lim
n→+∞
b−a
n
n−1
X
i=0
fa+ib−a
n=Zb
a
f(x) dx.
Proposition 54.5 — Cas particulier des fonctions définies sur [0 ,1].La formule ci-dessous devient
alors :
lim
n→+∞
1
n
n−1
X
i=0
fi
n=Zb
a
f(x) dx
Exemple 54.6 On veut étudier la limite de la somme :
n
X
i=1
1
n+i.
On considère l’application fdéfinie sur [0,1] par f(x) = 1
1+x. On a alors :
lim
n→+∞
1
n
n
X
i=1
1
1 + i
n
=Z1
0
1
1 + xdx
lim
n→+∞
n
X
i=1
1
n+i= ln 2.

54.2 Intégration par primitives 11
54.2 Intégration par primitives
Théorème 54.7 — Théorème fondamental du calcul intégral. Soit fune fonction continue sur un
intervalle I. Soit x0∈I. La fonction Fdéfinie sur Ipar :
F(x) = Zx
x0
f(t) dt
est l’unique primitive de fsur Is’annulant en x0. Autrement dit : F(x0)=0,Fest dérivable sur I
et pour tout réel x∈I,F0(x) = f(x).
Dv
•Démonstration — Soit x0∈I. Nous allons montrer que l’accroissement moyen F(x)−F(x1)
x−x1
admet une limite lorsque xtend vers xiet que cette limite est précisément f(x1). Évaluons :
F(x)−F(xi)
x−x1−f(x1)
=1
|x−x1|Zx
x0
f(t) dt−Zx1
x0
f(t) dt−(x−x1)f(x1) .
En utilisant la relation de Chasles et la formule d’intégration pour une fonction constante, on
peut écrire :
F(x)−F(x1)
x−x1−f(x1)
=1
|x−x1|Zx
x1
f(t) dt−Zx
x1
f(x1) dt .
Mais d’après la propriété de compatibilité avec l’addition :
Zx
x1
f(t) dt−Zx
x1
f(x1) dt=Zx
x1
(f(t)−f(x1)) dt
D’où : 
F(x)−F(x1)
x−x1−f(x1)≤1 |x−x1|Zx
x1|f(t)−f(x1)|dt.
Or, fest continue en x1donc admet une limite finie en x1. Cela signifie que tout intervalle
ouvert f(x1)contient toutes les valeurs de f(t)pour tassez proche de x1.
Soit ε∈R∗
+et I]f(x1)−ε , f(x1) + ε[. Alors, il existe un réel ηtel que pour tout t∈
]x1−η , x1+η[, on ait :
f(t)∈]f(x1)−ε , f(x1) + ε[.
D’où : 
F(x)−F(x1)
x−x1−f(x1)≤ε.
Comme εpeut être choisi aussi petit que voulu, on a bien :
lim
x→x1
F(x)−F(x1)
x−x1
=f(x1).
Donc Fest dérivable en x1, et F(x1) = f(x1). Et comme ce raisonnement est valable pour
tout x1∈I,Fest bien une primitive de fsur I. •
Ce théorème admet deux corollaires fondamentaux suivantes :

12 Leçon n°54 •Techniques de calcul d’intégrales
Corollaire 54.8 — Existence de primitives pour les fonctions continues. Toute fonction continue sur
un intervalle Iadmet des primitives sur I.
Corollaire 54.9 — Formule de Newton-Leibniz. Soit fune fonction continue sur un intervalle Iet F
une primitive de fsur I. Alors pour tous aet bdans I:
Zb
a
f(t) dt=F(b)−F(a).
Dv
•Démonstration — Soit x0∈Iet Gla primitive de fdéfinie par :
G(x) = Zx
a
f(t) dt.
On sait que deux primitives Fet Gdiffèrent d’une constante. Donc il existe un réel ktel que
pour tout :
F(x) = G(x) + k.
On a alors :
F(b)−F(a) = G(b)−G(a) = Zb
a
f(t) dt.
•
R54.10 La quantité F(b)−F(a)se note souvent [F(t)]b
a.
Exemples 54.11 1.
Z1
0
etdt=heti1
0= e −1.
2.
Z1
0
xn="xn+1
n+ 1#1
0
=1
n+ 1.
3.
Ze
2
1
xln xdt=Ze
2
1/x
ln xdt= [ln(ln(t))]e
2=−ln(ln(2)).
R54.12 Le choix de la primitive Fchoisie n’influe pas le résultat de l’intégrale. En effet, si Fet Gsont deux
primitives d’une même fonction fsur I, alors elles différent d’une constante. Les quantités F(b)−F(a)
et G(b)−G(a)sont donc égales.
Théorème 54.13 — Inégalité des accroissements finis. Soit fune fonction dérivable sur un intervalle
Itelle que f0soit continue sur I. S’il existe un réel Mtel que |f0| ≤ Msur Ialors : pour tous réels
aet bde I,ona:|f(b)−f(a)| ≤ M|b−a|.
Dv

54.3 Intégration par parties 13
•Démonstration — Pour a<b,ona:
|f(b)−f(a)|=Zb
a
f0(t) dt≤Zb
a|f0(t)|dt≤M(b−a)≤M|b−a|.
Pour a > b, ona :
|f(b)−f(a)|=Za
b
f0(t) dt≤Za
b|f0(t)|dt≤M(a−b)≤M|b−a|.
•
54.3 Intégration par parties
Définition 54.14 — Classe C1.On dit qu’une fonction est de classe C1sur un intervalle Isi elle est
dérivable sur Iet si sa dérivée f0est continue sur I.
Théorème 54.15 Soient uet vdeux fonctions de classe C1sur [a , b], alors :
Zb
a
u(t)v0(t) dt= [u(t)v(t)]b
a−Zb
a
u0(t)v(t) dt.
Dv
•Démonstration du théorème 54.15 —On sait que pour tout t∈[a , b]:
(uv)0(t) = u0(t)v(t) + u(t)v0(t).
En intégrant de aàb:
Zb
a
(u(t)v(t))0dt=Zb
a
u0(t)v(t) + u0(t)v0(t) dt
et d’après la linéarité de l’intégrale :
Zb
a
(u(t)v(t)0) dt=Zb
a
u0(t)v(t) dt+Zb
a
u(t)v0(t) dt
[u(t)v(t)]b
a=Zb
a
u0(t)v(t) dt+Zb
a
u(t)v0(t) dt.
D’où le théorème. •
Méthode 54.16 Pour intégrer par parties, il faut
— reconnaître, dans la fonction à intégrer, le produit d’une fonction uet d’une fonction dérivée
v0;
— appliquer la formule d’intégration par parties.
Exemples 54.17 1. Soit à calculer :
I=Z1
0
tetdt.