I = T I

1
M1 Physique Fondamentale (PF) 2013-2014
Magist`ere de Physique Fondamentale
Travaux Dirig´es Lasers n◦6
Exercice I : Pertes dans une cavit´e optique
M
1
M
2
a
m
p
l
i
f
i
c
a
t
e
u
r
"
M
3
T
I
=
T
I
L
3
3
R
3
R
2
R
1
d
i
o
d
e
o
p
t
i
q
u
e
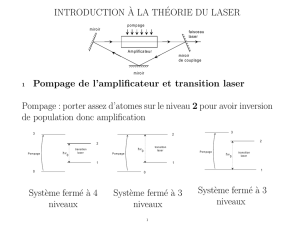
On consid`ere la cavit´e ci-contre consti-
tu´ee de 3 miroirs Mi(i = 1, 2, 3). La lon-
gueur optique totale de la cavit´e est d=
2,5 m, la longueur du milieu amplifica-
teur vaut ℓ= 1 m, et la longueur d’onde
de fonctionnement est λ0= 10,6 µm.
Les coefficients de r´eflexion des miroirs
pour l’intensit´e sont R1=R2= 0,99 et
R3= 0,97 (miroir de sortie).
Une diode optique impose le sens de propagation de la lumi`ere dans la cavit´e. On d´esigne par Ti
les facteurs de transmission des miroirs. La diffusion et l’absorption de ces miroirs sont suppos´ees
n´egligeables. Le milieu amplificateur est une cellule dont les extr´emit´es poss`edent chacune le facteur
de transmission T= 0,99 (on pourra poser R= 1 −T= 0,01 ≪1). La valeur relative des pertes
d’intensit´e sur un parcours complet de la cavit´e pour des raisons autres que celles mentionn´ees
pr´ec´edemment vaut η= 1,5 %.
1. Pour cette cavit´e, calculer le coefficient de pertes par unit´e de longueur du milieu amplificateur
(αP). Faire le d´eveloppement limit´e de son expression dans le cas Ti≪1 et 1−T≪1. Calculer
num´eriquement αPavec et sans approximation. L’approximation faite est-elle justifi´ee ?
2. L’amplificateur ´etant inactif, calculer la ’dur´ee de vie des photons dans la cavit´e’ (τc). Appli-
cation num´erique.
3. Quel est le nombre de tour moyen effectu´e par un photon dans la cavit´e ?
Exercice II : Puissance extraite d’un laser `a CO2continu
On r´ealise un laser avec la cavit´e optique d´ecrite dans l’exercice pr´ec´edent. Le milieu amplificateur
est une cellule contenant un m´elange de CO2,N2et He, sous une pression totale de P = 9 10−3
atmosph`ere `a temp´erature ambiante (300 K). La mol´ecule active est le dioxyde de carbone. La
transition laser se produit entre les niveaux 2et 1suppos´es non d´eg´en´er´es.
N
2
N
1
W
γ
N
0
1
2
0
1
γ
2
0
h
ν
0
A
Λ
P
1
/
τ
0
Pour la transition laser
Proba. par sec. pour l’´emission spontan´ee : A
Proba. par sec. pour l’´emission induite : W
Longueur d’onde dans le vide : λ0= 10,6 µm
Dur´ee de vie du niveau 2(hors collisions) : τ2= 4 10−3s
D´esexcitation 2→0 : γ20 = 50 s−1
Dur´ee de vie du niveau 1:τ1= 5 10−6s
Dur´ee de vie du niveau 0:τ0
Section efficace d’abs. pour l’onde laser : σ= 1,5 10−20 m2
Constante des gaz parfaits : R= 8,314 S.I.
L’´elargissement spectral est provoqu´e par l’effet Doppler et
par la pression. La pression produit une largeur spectrale
homog`ene ∆νh=β
2πPavec β 2π= 4 1010 Hz atm−1. La
largeur spectrale naturelle est n´egligeable.
On donne ´egalement : taux de pompage : ΛP= 5 1023 m−3s−1; diff´erence de population non
satur´ee : ∆N0= ΛP(1 −Aτ1)τ2; intensit´e de saturation : Is=hν0
σ(τ1+τ2−Aτ1τ2); diam`etre du

2
faisceau laser : 3 cm ; masse molaire du CO2: 44 g·Mol−1; facteur de transmission du miroir de
sortie : T3= 3 %.
1. Calculer num´eriquement ∆νhpuis l’´elargissement Doppler ∆νD. Ce milieu amplificateur est-il
`a ´elargissement spectral homog`ene dominant ou inhomog`ene dominant ?
2. Calculer num´eriquement ∆N0,Iset le coefficient d’amplification non satur´ee α0.
3. La longueur de l’amplificateur est ℓ= 1 m, on a ´evalu´e dans l’exercice -I- le coefficient de
pertes par unit´e de longueur du milieu amplificateur αP= 0,086 m−1. Quelle valeur num´e-
rique le gain total G=I(ℓ)
I(0) de l’amplificateur doit-il poss´eder pour que le laser fonctionne en
r´egime stationnaire ? Est-on en r´egime de pertes faibles ? Quelles sont les conditions de fonc-
tionnement Laser dans ce r´egime ? Relier le coeficient d’amplification satur´ee au coefficient
d’amplification non satur´ee, `a Iset `a l’intensit´e I(0) ´etablie en tout point de la cavit´e (rela-
tion de saturation). D´eterminer alors I(0) en fonction des donn´ees du probl`eme. Application
num´erique.
4. Le faisceau est suppos´e d’intensit´e uniforme sur sa section S. D´eterminer l’intensit´e ILextraite
de la cavit´e et la puissance PLcorrespondante (applications num´eriques).
5. R´evisions : retrouver `a partir de la description physique du syst`eme les expressions analy-
tiques de ∆N0et Is.
Exercice de r´evisions : syst`eme `a 4 niveaux pomp´e optiquement
Remarque importante : les syst`emes d’´equations `a r´esoudre pour la fin de cet exercice sont particu-
li`erement d´elicats, avec des calculs nettement plus difficile que ceux qui apparaˆıtront dans l’examen.
Il faut par contre bien maˆıtriser l’interpr´etation des hypoth`eses physiques conduisant `a la simplifi-
cation des ´equations.
On consid`ere un milieu mat´eriel repr´esent´e par un syst`eme `a 4 niveaux d’´energie poss´edant les
caract´eristiques suivantes :
– les quatre niveaux sont non d´eg´en´er´es, la population totale est not´ee N.
– le milieu est amplificateur pour la transition 2 ↔1. L’´emission spontan´ee et l’´emission induite
ont les probabilit´es par seconde et par atome Aet W. L’´elargissement spectral est purement
homog`ene. Le profil spectral de la transition est g(ν−ν0), de largeur ∆ν.
– le pompage est assur´e sur la transition radiative 3 ↔0 par une onde lumineuse intense d’´energie
proche de hν30 (’pompage optique’). L’´emission spontan´ee et l’´emission induite ont les probabilit´es
par unit´e de temps et par atome A30 et WP. Le pompage est assez puissant pour avoir A30 ≪WP.
– la transition 3 →2 est non radiative (d´esexcitation par collisions dans un gaz, couplage
avec les vibrations pour un cristal). Sa probabilit´e par seconde Γ est tr`es grande de sorte
qu’un atome arrivant sur le niveau 3 repart imm´ediatement vers le niveau 2 seulement
( (A30 +WP)≪Γ, N3≪N0).
– la transition 1 →0 est non radiative. Sa probabilit´e par seconde est not´ee γ.
h
ν
0
A
3
0
W
W
P
3
2
1
0
A
Γ
γ
Le syst`eme est ferm´e, N0+N1+N2+N3=
N. La diff´erence de population est not´ee ∆N=
N2-N1. D´eterminer la diff´erence de population
en r´egime stationnaire et l’intensit´e de satu-
ration en fonction des param`etres physiques du
syst`eme. Indications : exploiter soigneusement les
hypoth`eses physiques pour simplifier les ´equations
d’´evolution en les ramenant `a un syst`eme de deux
´equations `a deux inconnues N2et ∆N. R´esoudre
ce syst`eme pour identifier la solution ∆N`a l’´ecri-
ture ∆N0
1+ I
Is
.

3
M1 Physique Fondamentale (PF) 2013-2014
Magist`ere de Physique Fondamentale
Travaux Dirig´es Lasers n◦6, corrig´e succinct
Exercice I : Pertes dans une cavit´e optique
1. L’intensit´e restant apr`es un parcours complet de cavit´e s’´ecrit I(d) = I(0)R1R2R3T2(1 −η)
et correspond par d´efinition pour une cavit´e en anneau `a I(0) exp −αPℓ, d’o`u
αP=−1
ℓ[ln R1+ ln R2+ ln R3+ 2 ln T+ ln(1 −η)]num´eriquement, αP= 0,086 m−1
On simplifie cette expression pour ln Ri= ln(1 −Ti)≃ −Tilorsque Ti≪1 et ln T=
ln(1 −R)≃(−R) lorsque R≪1 pour obtenir
αP=1
ℓ[T1+T2+T3+ 2R+η] num´eriquement, αP= 0,085 m−1
Les deux r´esultats num´eriques sont tr`es proches, l’approximation est justifi´ee.
2. ´ Ecriture de l’´evolution de l’intensit´e sur un parcours complet de cette cavit´e lin´eaire (pertes
faibles) :
I(t+d
c0
) = I(t) exp −(αPℓ) = I(t) (1 −αPℓ)
I(t+d
c0
)−I(t) = = dI
dt ×d c0
qui vaut donc ici −αPℓ I(t)
dI
dt =−c0αPℓ dI(t) `a identifier `a −I(t) τc
par d´efinition de τc
d’o`u la ’dur´ee de vie des photons dans la cavit´e’ τc=d
c0αPℓ= 9,7 10−8s.
3. Un photon effectue un tour de cavit´e en d/c0secondes, par d´efinition de d, longueur optique
d’un tour de cavit´e. Il reste en moyenne un temps τcdans la cavit´e ce qui correspond ici `a
τcc0
d=9,7 10−8×3 108 2,5= 11,6 tours de cavit´e.
Exercice II : Puissance extraite d’un laser `a CO2continu
1. L’onde en interaction avec l’ensemble des atomes voit le coefficient d’amplification non satu-
r´ee :
α0(ν) = ∫νi dα0
i(ν)
α0(ν) = hν
cB∆N0∫g(ν−νi)P(νi−ν0)dνi
o`u g(ν−νi) d´ecrit l’absorption de la fr´equence νpar des atomes de r´esonance νi, avec le
mˆeme profil spectral quelle que soit νi. Cette fonction traduit donc les effets homog`enes, sa
largeur vaut ici ∆νh=β
2πP= 4 1010×9 10−3= 3,6 108Hz.
La fonction P(νi−ν0) traduit la distribution des fr´equences de r´esonance (effet inhomo-
g`ene) provoqu´ee par l’effet Doppler, c’est une gaussienne de largeur ∆νD=ν0
c0√8 ln 2 RT M=
1
10,6 10−6√8 ln 2 8,32 300 44 10−3= 5,3 107Hz.
L’application num´erique montre que ∆νDest petit devant ∆νhdonc l’expression pr´ec´edente
de α0(ν) est approximativement ´egale `a hν
cB∆N0g(ν−ν0), ce milieu amplificateur est `a
´elargissement homog`ene dominant.

4
2. ∆N0= ΛP(1 −Aτ1)τ2avec 1
τ2=A+γ20 ⇒A=1 τ2−γ20 = 200 s−1.
∆N0= 5 1023(1 −200 ×5 10−6)×4 10−3= 2 1021 m−3.
Is=hν0
σ(τ1+τ2−Aτ1τ2)= 6,62 10−34 3 108 10,6 10−6
1
1,5 10−20 ×1 5 10−6+ 4 10−3= 312 W ·m−2
α0=σ∆N0= 1,5 10−20×2 1021 = 30 m−1
3. En r´egime stationnaire, le gain total Gde l’amplificateur compense les pertes donc
Gexp −αPℓ= 1 et G= exp αPℓ= 1,09. Il est proche de 1, c’est un r´egime pertes faibles-gain
faible. Les conditions de fonctionnement Laser dans ce r´egime sont (i)ν=νm(fr´equence d’un
mode spectral de la cavit´e) et (ii)α=αP.
Justification : l’intensit´e lumineuse Iest uniforme et quasi constante dans la cavit´e donc le coefficient
d’amplification satur´ee αest lui aussi uniforme et constant. L’int´egration de l’´equation de propagation
de l’intensit´e 1
I
dI
dz =αavec αind´ependant de zdonne I(ℓ) = I(0) exp αℓ donc G= exp αℓ. On injecte
ce r´esultat dans le bilan d’intensit´e sur un parcours de cavit´e, Gexp −αPℓ= 1, pour d´eduire que le
coefficient d’amplification satur´ee αest ´egal `a αP.
L’´elargissement spectral dominant est l’´elargissement homog`ene. L’intensit´e conserve une va-
leur proche de I(0) en tout point de la cavit´e donc la relation de saturation s’´ecrit α=α0
1+ I(0)
Is
.
L’´egalit´e α=αPentraˆıne alors I(0) = Is(α0
αP−1) = 105W·m−2
4. Intensit´e et puissance laser extraites : IL=T3I(ℓ)= 3310 W·m−2.
PL=ILS= 3310 ×π(3 10−2
2)2= 2,3 W
Les lasers `a CO2produisent une puissance optique continue ´elev´ee, ils sont utilis´es dans
l’industrie pour des travaux d’usinage, de d´ecoupe ou de soudure, ou en m´edecine (’bistouri
laser’ qui d´ecoupe les tissus et caut´erise les vaisseaux sanguins).
5. Pour retrouver ∆N0et Is: ´ecrire les ´equations d’´evolution du syst`eme `a 3 niveaux, d´eterminer
en r´egime stationnaire ∆Net sa valeur ∆N0pour I= 0. Isest obtenue par l’identification
∆N
∆N0=1
1+ I
Is
. En adaptant les notations, ce calcul est analogue `a celui fait en cours pour le
syst`eme ouvert `a deux niveaux (Chap -I- §2.3 et 2.4).
Exercice de r´evisions : syst`eme `a 4 niveaux pomp´e optiquement
Les calculs complets sont faits en annexe du polycopi´e de cours (annexe chapitre -II-).
Synth`ese des ´equations en r´egime stationnaire, compte tenu des simplifications
dN3
dt = +WPN0−ΓN3= 0
dN2
dt = +Γ N3−W∆N−A N2= 0
dN1
dt = +W∆N+A N2−γ N1= 0
dN0
dt =−WPN0+γ N1= 0
N=N0+N1+N2
∆N=N2−N1
R´esultat :
∆N=(γ−A)WPN
(A γ +WPγ+WPA)
1
(1 + γ+2WP
A γ+WPγ+WPAW)
∆N0=(γ−A)WP
(Aγ +WPγ+WpA)N
et
Is(ν−ν0) = hν
σ(ν−ν0)
A γ +WPγ+WpA
γ+ 2WP
ou Is(ν−ν0) = c
B g(ν−ν0)
A γ +WPγ+WpA
γ+ 2WP