Recherche algorithmique d`antécédents par la fonction cosinus

Premi` ere S Mars 2016
Recherche algorithmique d’ant´ec´edents par la fonction cosinus.
Comparaison de deux m´ethodes : balayage & dichotomie.
Th` eme : Angles orient´ es & Trigonom´ etrie.
On s’int´eresse `a la fonction f:x∈[ 0 ; π]7→ cos x.
1. L’´etude de la d´eriv´ee de la fonction cosinus n’est pas au programme de cette ann´ee (elle est vue en
TS).
`
A l’aide du cercle trigonom´etrique et par des consid´erations g´eom´etriques simples, dresser le tableau
de variation de f.
2. Pr´eciser alors l’ensemble des r´eels poss´edant un ant´ec´edent par f.
´
Etant donn´e un r´eel y, on cherche `a savoir s’il existe un ant´ec´edent αde ypar fet, le cas ´ech´eant,
on souhaite en obtenir un encadrement d’amplitude aussi petite qu’on veut.
Pour cela, on propose l’algorithme Algo 1 (cf page 2) ´ecrit dans le langage AlgoBox.
3. a) Que signifie floor(n),abs(y),Math.PI et pow(10,-n) (cf lignes 9, 15, 22 et 24) ?
b) Justifier les lignes 15, 16 et 17.
c) Recopier et compl´eter les pointill´es (cf page 2) du texte qui explique le rˆole de Algo 1.
4. a) Dans cette question, on suppose que l’utilisateur a choisi n= 1. Donner un majorant C1du
nombre de passages dans la structure it´erative «tant que ».
b) Pour un entier nquelconque, g´en´eraliser la question pr´ec´edente et d´eterminer, en fonction de n,
un majorant Cndu nombre de passages dans la structure it´erative «tant que ».
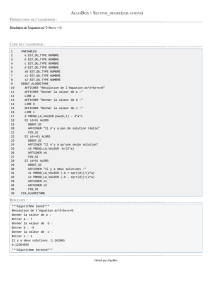
5. On consid`ere l’algorithme Algo 2 (cf page 2). Il s’agit d’une modification d’Algo 1.
a) Pr´eciser les modifications effectu´ees. Quel renseignement suppl´ementaire retourne cet algorithme ?
b) Ex´ecuter cet algorithme afin de compl´eter le tableau suivant :
y−1−0,8−0,1 0,5
n3 5 4 6
a
b
compteur
6. La question pr´ec´edente souligne le fait que plus l’entier nchoisi est grand (c-`a-d plus la pr´ecision
exig´ee de l’encadrement de l’ant´ec´edent αde ypar fest forte), plus le nombre de passages dans la
boucle «tant que »devient tr`es grand. . .
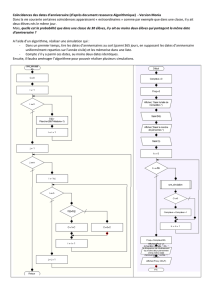
Afin d’optimiser l’efficacit´e de l’algorithme (et ainsi, de demander moins de calculs `a la machine), on
envisage l’algorithme Algo 3 (cf page 3).
a) Ex´ecuter cet algorithme afin de compl´eter le tableau suivant :
y−1−0,8−0,1 0,5
n3 5 4 6
a
b
compteur
b) Dans Algo 1, on «avance »pas `a pas de 0vers π, avec un pas de 10−n. Dans Algo 3, le principe
est tout autre. Nous avons d´ej`a rencontr´e un tel proc´ed´e. Comment s’appelle une telle m´ethode ?
c) Comparer alors Algo 2 et Algo 3 (on pourra comparer leur pr´ecision, leur efficacit´e. . .).
Corrig´e disponible sur http://tivomaths.free.fr/ - 1/3-L
A
T
E
X 2ε

AlgoBox http://www.xm1math.net/algobox/index.html
AlgoBox
Algo 1 Algo 2
1 VARIABLES
2 y EST_DU_TYPE NOMBRE
3 n EST_DU_TYPE NOMBRE
4 x EST_DU_TYPE NOMBRE
5 a EST_DU_TYPE NOMBRE
6 DEBUT_ALGORITHME
7 LIRE y
8 LIRE n
9 SI (floor(n)!=n) ALORS
10 DEBUT_SI
11 AFFICHER "n doit ^etre un entier !"
12 FIN_SI
13 SINON
14 DEBUT_SINON
15 SI (abs(y)>1) ALORS
16 DEBUT_SI
17 AFFICHER "pas de solution"
18 FIN_SI
19 SINON
20 DEBUT_SINON
21 x PREND_LA_VALEUR 0
22 TANT_QUE (cos(x)>=y ET x<=Math.PI) FAIRE
23 DEBUT_TANT_QUE
24 x PREND_LA_VALEUR x+pow(10,-n)
25 FIN_TANT_QUE
26 a PREND_LA_VALEUR x-pow(10,-n)
27 AFFICHER "a="
28 AFFICHER a
29 AFFICHER "b="
30 AFFICHER x
31 FIN_SINON
32 FIN_SINON
33 FIN_ALGORITHME
1 VARIABLES
2 y EST_DU_TYPE NOMBRE
3 n EST_DU_TYPE NOMBRE
4 x EST_DU_TYPE NOMBRE
5 a EST_DU_TYPE NOMBRE
6 compteur EST_DU_TYPE NOMBRE
7 DEBUT_ALGORITHME
8 LIRE y
9 LIRE n
10 SI (floor(n)!=n) ALORS
11 DEBUT_SI
12 AFFICHER "n doit ^etre un entier !"
13 FIN_SI
14 SINON
15 DEBUT_SINON
16 SI (abs(y)>1) ALORS
17 DEBUT_SI
18 AFFICHER "pas de solution"
19 FIN_SI
20 SINON
21 DEBUT_SINON
22 x PREND_LA_VALEUR 0
23 compteur PREND_LA_VALEUR 0
24 TANT_QUE (cos(x)>=y ET x<=Math.PI) FAIRE
25 DEBUT_TANT_QUE
26 x PREND_LA_VALEUR x+pow(10,-n)
27 compteur PREND_LA_VALEUR compteur+1
28 FIN_TANT_QUE
29 a PREND_LA_VALEUR x-pow(10,-n)
30 AFFICHER "a="
31 AFFICHER a
32 AFFICHER "b="
33 AFFICHER x
34 AFFICHER "Nombre de passages : "
35 AFFICHER compteur
36 FIN_SINON
37 FIN_SINON
38 FIN_ALGORITHME
Question 3.c) Compl´eter les phrases suivantes qui expliquent le rˆole de l’algorithme Algo 1.
`
A partir de la donn´ee d’un r´eel yet d’un entier naturel n,Algo 1 pr´ecise s’il existe un . . . . . . . . . . . . ..
......................................................................................................
Si un tel . . . . . . . . . . . . . . . . existe (notons-le α), Algo 1 retourne alors deux r´eels aet b(a < b) tels que :
®...........................
b−a=................
Corrig´e disponible sur http://tivomaths.free.fr/ - 2/3-L
A
T
E
X 2ε

Algo 3
1 VARIABLES
2 y EST_DU_TYPE NOMBRE
3 n EST_DU_TYPE NOMBRE
4 x EST_DU_TYPE NOMBRE
5 a EST_DU_TYPE NOMBRE
6 b EST_DU_TYPE NOMBRE
7 m EST_DU_TYPE NOMBRE
8 compteur EST_DU_TYPE NOMBRE
9 DEBUT_ALGORITHME
10 LIRE y
11 LIRE n
12 SI (floor(n)!=n) ALORS
13 DEBUT_SI
14 AFFICHER "n doit ^etre un entier !"
15 FIN_SI
16 SINON
17 DEBUT_SINON
18 SI (abs(y)>1) ALORS
19 DEBUT_SI
20 AFFICHER "pas de solution"
21 FIN_SI
22 SINON
23 DEBUT_SINON
24 a PREND_LA_VALEUR 0
25 b PREND_LA_VALEUR Math.PI
26 compteur PREND_LA_VALEUR 0
27 TANT_QUE (b-a>pow(10,-n)) FAIRE
28 DEBUT_TANT_QUE
29 m PREND_LA_VALEUR (a+b)/2
30 SI (cos(m)>y) ALORS
31 DEBUT_SI
32 a PREND_LA_VALEUR m
33 FIN_SI
34 SINON
35 DEBUT_SINON
36 b PREND_LA_VALEUR m
37 FIN_SINON
38 compteur PREND_LA_VALEUR compteur+1
39 FIN_TANT_QUE
40 AFFICHER "a="
41 AFFICHER a
42 AFFICHER "b="
43 AFFICHER b
44 AFFICHER "Nombre de passages : "
45 AFFICHER compteur
46 FIN_SINON
47 FIN_SINON
48 FIN_ALGORITHME
Corrig´e disponible sur http://tivomaths.free.fr/ - 3/3-L
A
T
E
X 2ε