Cours ppt

Chapitre 02 : Prospection
électromagnétique
1UDBKM-FST-SM-M1PDG: Prospection E.M

Chapitre 02 : Prospection électromagnétique
I. Introduction :
Toute méthode de prospection utilisant les champs électromagnétiques
artificiels ou naturels, générés par des courants variables dans le temps,
est une méthode de prospection électromagnétique.
Ces méthodes sont intéressantes quand il s’agit d’une reconnaissance
rapide, d’une détection sommaire ou d’une simple découverte de zones
d’anomalies.
Complexes et difficiles pour l’interprétation quantitative en 1D, 2D et 3D,
Limitation de leur profondeur d’investigation qui diminue avec
l’augmentation de la fréquence utilisée.
2UDBKM-FST-SM-M1PDG: Prospection E.M

Tous les appareils de prospection électromagnétique répondent à une grande
variété de conducteurs tant naturels qu’artificiels, qui peuvent se classer
comme suit :
1. Conducteurs superficiels :
a. Mort-terrain (terrain
marécageux, argileux)
b. Fonds de lacs et lits de cours
d’eau
c. Formations conductrices (argiles)
d. Topographie (relief)
2. Conducteurs dans la roche en place
a. Graphite
b. Sulfure massifs
c. Magnétite massive
d. Zones de cisaillement et failles
e. Péridotite serpentinisée*
3. Conducteurs artificiels
a. Réservoirs métalliques
b. Conduites et déchets
métalliques
c. Pipe-lines
d. Voies ferrées
e. Lignes à haute tension
3
*: Roche constituée principalement de cristaux d’olivine et
de pyroxènes qui peut devenir de la serpentinite sous l’effet
de la chaleur et d’une hydratation
UDBKM-FST-SM-M1PDG: Prospection E.M

1.2. L’induction électromagnétique:
En régime variable : un champ magnétique
variable engendre un champ
électrique (l’induction électromagnétique), alors
que dans un conducteur, un champ électrique
crée un courant, lequel crée un champ
magnétique (loi d’Ampère)
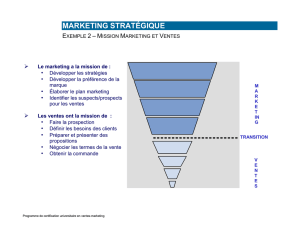
La méthode de prospection électromagnétique
(E.M) fait intervenir simultanément les trois
processus physiques distincts (figure ci-contre) :
UDBKM-FST-SM-M1PDG: Prospection E.M 4
1. La production d’un champ magnétique primaire qui varie avec le temps;
2. La naissance de courants induits  (courants de Foucault) dans tous les conducteurs sur
lesquels agit ce champ primaire ;
3. La détection de ces conducteurs par la mesure des champs magnétiques secondaires 
créés par les courants de Foucault.
Figure 1. Représentation schématique de la prospection EM

1.2. L’induction électromagnétique:
L’amplitude des courants induits dans un corps conducteur dépend de plusieurs facteurs, à peu près
équivalents, qui sont :
- les propriétés électriques du conducteur  ;
- les dimensions et la forme du conducteur  ;
-la fréquence du champ primaire  ;
-l’emplacement du conducteur / instruments géophysiques .
La figure 2 illustre bien ces éléments clés : les courants de Foucault champ magnétique créé 
UDBKM-FST-SM-M1PDG: Prospection E.M 5
Figure 2. Induction électromagnétique. A) Vue en perspective. B) Vue suivant la coupe A-B.