Un algorithme est une liste finie de processus élémentaires

ALGORITHMIQUE DMARTIN_LAH
Définition : Un algorithme est une liste finie de processus élémentaires, appelées instructions élémentaires, amenant à la résolution d’un problème.
De façon générale, dans un algorithme, on peut distinguer :
• Trois étapes : 1. Entrée des données 2. Traitement des données 3. Sortie des résultats
• Quatre familles d’instructions : 1. Entrée/Sortie de données 2. Affectation d’une valeur à une variable 3. Conditionnelle 4. Boucles
Langage courant Algobox Python TI NSPIRE TI 82 … Casio
Entrée de données L’utilisateur entre la
valeur de la variable A Lire_variable_A
A=Input(« A= »)
[chaîne de caractères]
A=int(input()) [entier]
A=float(input()) [réel]
Define
Fonction(A)=prgm
Local A
[les variables utilisateur
sont définies dans le
nom de la fonction]
Input A
Prompt A ?  A
Sortie de données Le programme affiche
la valeur de la variable
A
Afficher_variable_A
Print(A)
Print(A,end= “”) [affichage
en ligne]
Disp(A) Disp A A
Affec
ta
tion d’une
valeur à une variable On donne la valeur 1 à
la variable A Affecter_valeur_variable_A(1)
A=1 A :=1 1 → A
A := 1 1  A
Instruction
Conditionnelle
Si une condition
COND est vérifiée le
programme effectue
les instructions INST1,
sinon il effectue les
instructions INST2
 Si (COND) alors
| Début_si
| INST1
| Fin_si
 Sinon
| Début_sinon
| INST2
| Fin_sinon
If COND :
INST 1
Else :
INST2
[c’est l’indentation – retrait des
lignes - qui identifie le bloc
d’instructions dépendant de
chaque commande]
If COND Then
INST1
Else
INST2
EndIf
[indentation]
If COND
Then INST1
Else INST2
End
If COND
Then INST1
Else INST2
IfEnd
Boucle
conditionnelle
Tant qu’une condition
COND est vérifiée le
programme effectue
les instructions INST
 Tant que (COND) Faire
| Début_tant_que
| INST
| Fin_tant_que
While COND :
INST
While COND
INST
EndWhile
While COND
INST
End
While COND
INST
WhileEnd
Boucle itérative Le programme
effectue N fois les
instructions INST.
 Pour i allant de 1 à N Faire
| Début_pour
| INST
| Fin_pour
For i in range(1,N+1) :
INST
For I,1,N
INST
EndFor
For(i,1,N)
INST
End
For i 1 to N
INST
Next

ALGORITHMIQUE DMARTIN_LAH
1. Dans les algorithmes suivants caractériser chaque type d’instruction (utiliser un code couleur) :
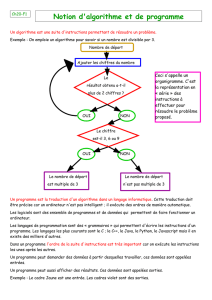
A) Ecrire un nombre
Multiplier ce nombre par 2
Elever le résultat au carré
Retrancher 4
Ecrire le résultat final
B) Choisir un nombre réel
S’il est supérieur à 0
| Ajouter 1 à ce nombre
Sinon
| Elever ce nombre au carré
| Ajouter 1
Ecrire le résultat final
C) Variables
| x, y nombres entiers
Début
Pour x allant de –5 à 5
| x²  y
| y – 4  y
| Afficher le point (x ; y)
Fin
D) Entrée : Deux entiers naturels a et b
Début : Tant que b > 0 Faire :
| Affecter r au reste de la division euclidienne de a par b
| Affecter a à la valeur de b
| Affecter b à la valeur de r
Fin_tant_que
Sortie : Afficher a
2. Faire fonctionner A et B avec une ou deux valeurs choisies.
3. Que fait l’algorithme C ?
4. Dire à quelle fonction correspond chacun des trois algorithmes ci-dessus.
5. Réécrire les algorithmes A et B en pseudo-code (langage proche de la machine, comme dans le C).
6. Ecrire l’algorithme en pseudo-code de la fonction suivante : f(x) = – +3 ≥ 1
3−  < 1
7. a. Faire tourner l’algorithme D pour a = 24 et b = 15 puis pour a = 45 et b = 13.
b. Que fait cet algorithme ?
c. Programmer cet algorithme dans le langage de votre choix.
8. Ecrire un algorithme qui permute les valeurs de deux variables.
9. Méthode de Monte Carlo :
ABCD est un carré de côté 1 et la surface colorée un quart de cercle de rayon 1.
a. On considère un point M de coordonnées (a ; b) avec a et b deux nombres aléatoires
de l’intervalle [0 ; 1]. A quelle surface appartient le point M ?
b. Donner une condition pour que M appartienne au quart de cercle.
c. Construire et programmer l’algorithme suivant :
Entrée : Un nombre N de points à placer aléatoirement dans le carré.
Traitement : Compter le nombre de points k parmi ces N points qui se situent dans le quart de cercle.
Sortie : Le rapport k/N.
d. Reproduire et compléter le tableau suivant :
Placer les résultats à 10
–4
près.
e. Calculer l’aire exacte du quart de disque. En donner une approximation à 10
–4
près. Que constatez-vous ?
Cette méthode d’approximation d’une aire s’appelle méthode de Monte Carlo, elle est attribuée au mathématicien Polonais Stanislaw Ulam.
N 10 100 1000 10000 100000
k/N

ALGORITHMIQUE DMARTIN_LAH
10. Algorithme de Syracuse
11. Algorithme de Babylone, algorithme de Héron
12. La machine à résoudre : ax + b = 0.
Prolongement : la machine à résoudre ax + b = cx = d