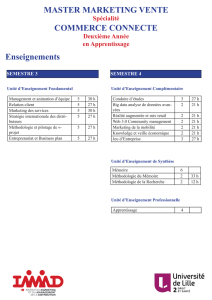
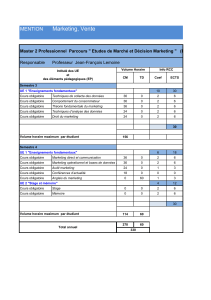
cours en ppt

1
2010-11, GEII semestre 3 Mathématiques
Intégrales
1 - Intégrale simple
2 - Deux directions de généralisation
3 - Techniques de calcul
4 - Intégrale multiple
Bruno Rossetto, bureau A 37, tél. [phone]
et 04 94 14 27 26
email : [e-mail]
site : http://rossetto.univ-tln.fr

2
2010-11, GEII semestre 3 Mathématiques
Somme discrète
•Distance parcourue lorsque la vitesse varie par paliers
t0tn
titi+1
v(t)
v(ti)
h
t
di= v(ti) . h
Distance parcourue durant l’intervalle
de temps
ht tavec ,t,t i1i1ii 
n
1i in dD: totaleDistance
) v(t.h Dn
1i in 
diest l’aire du rectangle hachuré.
Dnest la somme des aires des rectangles

3
2010-11, GEII semestre 3 Mathématiques
Somme continue
•Distance parcourue lorsque la vitesse varie de manière continue
) v(t.h lim D lim totaleDistance n
1i i
n
n
n
a = t0b = tn
tt+h
v(t)
v(ti)
h
t

4
2010-11, GEII semestre 3 Mathématiques
Intégrale simple (1)
• Intégrale de Riemann : l’idée
a = t0b = tn titi+1
v(t)
v(ti)
h
t
ntt nab
h0n 
i1i tth  
Aire = h . f(ti)
n
n
b
a
Rlimv(t)dt Intégrale 
) v(t.h R totaleAire n
1i in 
L’intégrale est l’aire algébrique comprise entre la courbe, l’axe des t et les bornes
(Rnest appelé somme de Riemann)

5
2010-11, GEII semestre 3 Mathématiques
Intégrale simple (2)
• Intégrale de Riemann : d’autres idées
a = t0b = tn titi+1
f(t)
f(ti+1)
h
t
ntt nab
h0n 
i1i tth  
Aire = h . f(ti+1)
La somme de Riemann tend vers la même limite, mais par valeurs supérieures, cette fois-ci.
)f(t .h R' totaleAire n
1i 1in 
n
n
b
a
R'limf(t)dt Intégrale 
(R’n: somme de Riemann)