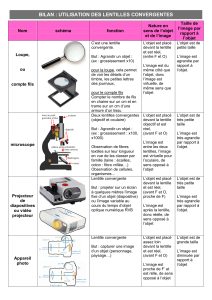
Focométrie des lentilles minces

1
BOUSQUET Juliette
BERGEONNEAU Morgane
TP n°1 : Focométrie des lentilles minces
Objectifs du TP : Déterminer la distance focale d’une lentille mince (convergente ou
divergente) à l’aide de différentes méthodes classiques.
Matériel utilisé : Une source lumineuse, deux lentilles convergentes L1 et La de distance
focales respective 300 mm et 150 mm, un objet en forme de T, un miroir plan et un
écran. Ces différents éléments peuvent être placés sur l’axe optique.
I. Identification rapide des lentilles
Nous avons constaté qu’à travers la lentille L1 et La, l’image d’une page de texte était
plus grande, et l’image de l’objet observé à l’infini était renversée. C’est deux lentilles
étaient donc convergentes.
II. Mesure de la distance focale d’une lentille mince convergente
A. Relation de conjugaison de Descartes
Manipulation : Lors de cette manipulation nous avons aligné sur l’axe optique un objet
(AB), une lentille L1 et un écran. Nous avons réalisé six mesures de position O et A’ :
cinq correspondant à la réalisation d’une image réelle et une correspondant à la
réalisation d’une image virtuelle.
Image réelle
image virtuelle
Position A (cm)
40
66
Position O (cm)
90
100
110
115
125
100
 (cm)
-50
-60
-70
-75
-85
-34
1/ (m-1)
-2
-1,67
-1,43
-1,33
-1,17
-2,94
(1/) (m-1)
4,00E-03
2,78E-03
2,04E-03
1,78E-03
1,38E-03
8,66E-03
Position A' (cm)
183
171
170
171,5
177,5
140
' (cm)
93
71
60
56,5
52,5
-40
1/' (m-1)
1,08
1,41
1,67
1,77
1,9
-2,5
(1/') (m-1)
1,16E-02
1,98E-02
2,78E-02
3,13E-02
3,63E-02
-6,25E-02

2
Calcul de (1/) :
 Il faut tout d’abord calculer l’incertitude . On sait  est une incertitude de
lecture sur deux points (O et A) soit 0,5*2 (demi graduation). Donc 
=0,001 m
 On en déduit ensuite p et  pour chaque point.
Ex : 1= -50 cm = -0,50 m donc  = -0,501 m
= -0,499 m
 On calcule enfin (1/p)
Ex : D(1/1) = (1/p -1/ )/2 = (1/(-0,501)-1/(-0,499))/2 = 0,004 m
Calcul de (1/’) :On réitère cette technique pour calculer (1/’)
En rédigeant le rapport, nous nous sommes rendu compte que nous avions fait de
mauvais calculs lors de la séance de TP. En effet, nous pensons que nous nous sommes
trompées lors des conversions. On a donc rectifié lors de la rédaction de ce rapport.
Pour effectuer ce graphique nous n’avons pas tenu compte de la dernière valeur (image
virtuelle) car elle faussait tous les résultats. Cela doit être dû à une erreur de
manipulation.
D’après le graphique et la relation de Descartes nous obtenons une droite de la forme
=
+
. L’ordonnée à l’origine est donc 1/f’. il nous suffit donc de prendre l’inverse
pour en déduire f’.
= 3,0936 => f’=0,32 m (attention ce résultat diffère de celui rendu lors de la séance
de TP car le graphique a été réalisé avec les bonnes valeurs)

3
Calcul de f’ :
On effectue ce calcul pour les 6 mesures, et on prend la plus grande valeur pour
maximiser l’incertitude.
Df'1=5,16.10-3m
Df'2=4,76.10-3m
Df'3=4,82.10-3m
Df'4=4,91.10-3m
Df'5=5,01.10-3m
Df'6=1,49.10-2m
Donc  
Vérification de la formule de grandissement : On vérifie la formule de grandissement en
l’appliquant à une de nos mesures.
Les valeurs sont donc très proches. Ainsi la formule de grandissement est vérifiée.