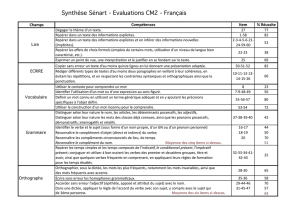
Lois des exposants IV

Lois des exposants IV
1. Comment interpr´eter les expressions o`u il y a un exposant qui est une fraction.
•Nous analysons ce qui se passe dans l’exemple suivant o`u nous g´en´eralisons encore
une fois le principe sur la multiplication des nombres avec des exposants.
91
2×91 2= 91 2+1 2
= 91
= 9
•Donc 91
2est un nombre qui, multipli´e par lui-mˆeme, ´egale 9.
–Nous savons que le nombre qui, multipli´e par lui-mˆeme, ´egale `a 9 c’est √9 =
3.
–Nous ´enon¸cons l’hypoth`ese suivante: a
1
2=√apourvu que a≥0.
–Nous illustrons notre hypoth`ese dans un deuxi`eme exemple.
161
2×161 2= 161 2+1 2
= 161
= 16
Donc 16 1
2=√16 = 4.
•Nous ´enon¸cons formellement le principe suivant: pour tout nombre a≥0
a
1
2=√a
–Il est facile de voir que 491
2= 7. Mais que faire avec l’expression 2 1 2?
∗Normalement nous laissons ce genre d’expression telle quelle, c’est-`a -
dire, sous la forme 2 1
2ou √2.
∗Dans le concept intitul´e Nombres irrationnelles sur la page des Concepts
vous verrez que 21
2est un nombre irrationnelle.
∗Vous y constaterez qu’il n’est pas possible d’´ecrire la racine carr´ee de 2
autrement.
1

2. Comment interpr´eter une expression telle que 271
3.
271
3×271 3×271 3= 91 3+1 3+1 3
= 271
= 27
•Donc 27 1
3est un nombre qui, multipli´e par lui-mˆeme trois fois, ´egale 27.
•Il s’agit donc de la racine cubic de 27. C’est-`a -dire 27 1
3=3
√27 = 3.
•Nous ´enon¸cons l’hypoth`ese suivante: a
1
3=3
√apour tout nombre a(y inclus les
nombres n´egatifs).
•Nous illustrons notre hypoth`ese dans un deuxi`eme exemple.
641
3×641 3×641 3= 161 3+1 3+1 3
= 641
= 64
Donc 64 1
3=3
√64 = 4.
–Encore une fois, lorsque nous avons une expression telle que 3 1
3nous laissons
ce genre d’expression telle quelle, c’est-`a -dire, sous la forme 31
3ou 3
√3.
∗Le nombre 31
3est un nombre irrationnel.
•Nous ´enon¸cons de fa¸con formelle le principe suivant: Pour tout nombre aet
nombre entier n
a
1
n=n
√a
–` A noter: Si le nombre aest n´egatif l’expression a
1
nn’est bien d´efinie que
dans le cas ou l’entier nest impair.
–Par exemple l’expression (−9)1
2n’a pas de valeur dans notre syst`eme num´erique.
2

3. Comment interpr´eter une expression telle que 272
3.
•Nous allons g´en´eraliser le principe (an)m=anm (voir le concept Exposants III)
pour que les puissance net mpuissent prendre la forme de fractions.
–Par exemple:
272
3= (27 1 3)2
= 32
= 9
–Voici un deuxi`eme exemple:
642
3= (64 1 3)2
= 42
= 16
•Nous ´enon¸cons de fa¸con formelle le principe suivant: Pour tout nombre aet
nombre entier net m
a
n
m= (a
1
m)n= ( m
√a)n
–` A noter: Si le nombre aest n´egatif l’expression a
n
m= ( m
√a)nn’a une valeur
dans notre syst`eme num´erique que dans le cas ou l’entier mest impair.
c
Club Pythagore, 2007
3