Exercices 7

MPSI CHAPITRE 7
EXERCICES
7-1 Association de miroirs
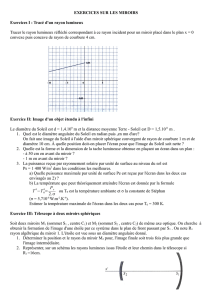
On réalise un système optique centré constitué par l'association du miroir concave M1, de centre C1 de sommet S1, et du
miroir M2, de centre C2, de sommet S2, de même axe optique, disposés comme sur la figure ci-dessus.
Le miroir M1 est percé d'un petit trou permettant à la lumière de le traverser près de son sommet, mais qui ne modifie pas
ses propriétés.
Les distances focales f1 et f2 des deux miroirs sont telles que |f1| = 3 m et |f2| = 2.0 m. On note d =
21SS
. (Le dessin ci-
dessus n'est pas une construction exacte).
1) Déterminer d pour que tout rayon incident, parallèle à l'axe optique et réfléchi par les deux miroirs, passe par S1.
2) Vérifier le calcul par une construction graphique à l'échelle 0,02 pour les segments parallèles à l'axe optique. (L'échelle
dans la direction perpendiculaire à l'axe optique sera prise bien plus grande).
7-2 Cavité confocale
Une cavité confocale est constituée de deux miroirs identiques concaves M1 et M2 face à face, de même rayon R, de
même axe optique  et dont les foyers sont confondus. On place un objet AB à l'intérieur de la cavité perpendiculairement à .
1) Construire géométriquement les quatre images successives obtenues, la première réflexion ayant lieu sur M2. Le résultat
dépend-il de la position de l'objet AB ?
2) On considère un rayon lumineux, incliné d'un angle 1 sur l'axe optique, émis d'un point B et dont le support passe par le
point I1 de M1 distant de y0 de l'axe optique.
Exprimer en fonction de 1, y0 et R dans les conditions de Gauss, les angles 2, 3, 4 que font les rayons réfléchis avec 
à l'issue respectivement de la 1ère, 2ème puis 3ème réflexion.
3) Conclure quant à la localisation du rayon à l'intérieur de la cavité optique.
C1S2
+
S1
C2
(M2)
(M1)
C1S2
+
S1 S1
C2
(M2)
(M1)
S2+
S1
(M1)(M2)
A
B
S2+
S1
(M1)(M2)
A
B

7-3 Télescope Hipparcos (D'après écrit Mines sup 2000 filière PCSI option PC)
On propose de modéliser le télescope d'Hipparcos par un miroir concave MC de rayon R = 2 800 mm avec un miroir plan
de renvoi (voir figure ci-dessous). On note S le sommet du miroir concave. La lumière subit deux réflexions et passe par un orifice
dans le miroir concave pour atteindre le détecteur. Celui-ci est constitué d'une grille et de cellules CCD permettant de repérer la
position de l'image. La grille comporte N = 2 688 fentes équidistantes de L = 8,2 µm.
On considère une étoile visée dans la direction Sx. L'axe Sx est orienté vers l'étoile.
1) Déterminer l'abscisse x de l'image E1, de l'étoile E donnée par le miroir MC
2) On note a la distance séparant le miroir plan et le sommet du miroir concave. Déterminer une condition sur a pour que
l'image finale E2 se forme sur le détecteur placé à l'arrière du miroir concave.
3) Déterminer la largeur angulaire C du champ observé. Calculer C en degré.
4) En réalité, Hipparcos réalise une mesure de position relative des étoiles. Le télescope vise deux directions symétriques
par rapport à Sx présentant un angle  = 58 °. C'est un système de deux miroirs plans M1, M2 qui permet d'obtenir les images des
deux étoiles sur le détecteur (voir figure ci-dessous). Le télescope tourne autour d'un axe de direction fixe Sz.
Déterminer l'angle 0 des miroirs M1 et M2 avec l'axe Sx du télescope.
5) Déterminer le déplacement angulaire 1, d'un rayon lumineux réfléchi par le miroir M1 lorsque le satellite tourne d'un
angle . Préciser le sens de déplacement des rayons réfléchis par M1 et M2.
S
(MP)
(MC)y
xS
(MP)
(MC)y
SS
(MP)
(MC)y
x
xS
(MP)
(MC)y
(M1)
(M2)
E
E'
0
sens de rotation
du satellite
xS
(MP)
(MC)y
(M1)
(M2)
E
E'
0
sens de rotation
du satellite
SS
(MP)
(MC)y
(M1)
(M2)
E
E'
0
sens de rotation
du satellite