DTL de Physique-chimie N°3

CLASSE DE TERMINALE D.T.L. de PHYSIQUE-CHIMIE N°4
P.E. BONNEAU ANNEE 2004-2005 Page 1/4
Nom : Classes de TS2
Prénom : le 11/12/2004
D.T.L. de Physique-chimie N°3
Durée : 3H00 - Coefficient 2
Calculatrice non autorisée – Documents interdits
Ce sujet comporte 9 pages
TOUTES LES PAGES DU SUJET DOIVENT OBLIGATOIREMENT ETRE RENDUES
La rédaction s’effectue sur le sujet lui-même.
Exercice n°1 (4,5 points) : A propos de l’électrolyse
Cet exercice est un QROC (questions à réponses ouvertes et courtes). A chaque affirmation,
vous répondrez par VRAI ou FAUX. Toute réponse doit être accompagnée de justifications ou
de commentaires brefs (définitions, calculs, exemples ou contre- exemples...).
I ) Dans l'industrie monétaire, on cuivre une rondelle d'acier appelée flan pour obtenir
certaines pièces de monnaie comme les pièces de 1, 2 et 5 centimes d'euros.
1) L'électrolyse est une transformation chimique forcée car elle s'effectue en sens inverse
du sens de la transformation spontanée.
2) La demi-équation électronique modélisant la réaction qui a lieu au niveau de la rondelle
métallique est Cu2+(aq) + 2 e- = Cu (S) car il faut que du métal cuivre soit formé et déposé
dessus.
3) Cette rondelle est reliée à la borne - du générateur de tension continue car les électrons
sortent de cette borne et arrivent à la rondelle pour réagir avec les ions Cu2+ de la solution.
4) Ce « flan » constitue la cathode de l'électrolyseur car il s'y produit la réduction qui est
toujours cathodique.
5) Pour maintenir constante la concentration en ions cuivre II (Cu2+) dans l'électrolyte, on
place une électrode de cuivre à l'anode pour y produire l'oxydation du métal cuivre en ions
Cu2+ .
II ) En fait, le cuivrage s'effectue, à 60°C, sur un tonneau dans lequel peut se trouver
80 kg de rondelles d'acier, soit environ 18000 rondelles.
1) La masse de cuivre à déposer, sur une rondelle d'acier, est de :
V = S . e = 9,2.10-4 x 25.10-6 = 2,3.10-8 m3
m = r . V = 8960 x 2,3.10-8 = 2,06.10-4 kg = 0,206 g = 206 mg
(en respectant le nombre de chiffres significatifs , on devrait indiquer 2,1.10-4 kg)
2) Pour le lot de 80 kg, il faut donc une quantité de cuivre d'environ :
mtotal = 18 000 m = 18 0000 x 2,06.10-4 = 3,71 kg ; ( il y a 18 000 rondelles à cuivrer)

CLASSE DE TERMINALE D.T.L. de PHYSIQUE-CHIMIE N°4
P.E. BONNEAU ANNEE 2004-2005 Page 2/4
3) La quantité d'électricité qui doit circuler pour réaliser ce dépôt est de :
D'après la demi-équation, n(e-) = 2 n(Cu)formé = 2 m(Cu)/M(Cu) = 2 x 3,71.103/63,5 = 117 mol
Q = n(e-) . F = 117 x 96500 = 1,13.107 C
4) L’intensité du courant est constante et égale à 1200 A. La durée de l'opération est donc
d'environ :
Q = I . t => t = Q / I = 1,13.107 / 1200 = 9,42.103 s = 157 min
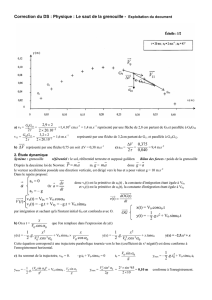
Exercice n°2 (7,25 points) : Satellites de Jupiter
I.1)
2) a) Un mouvement uniforme se fait à une vitesse constante.
b) Un référentiel « jupitocentrique » est constitué du centre de Jupiter et de trois étoiles
lointaines considérées comme fixes .
Dans ce référentiel supposé galiléen, on applique la deuxième loi de Newton au satellite
Europe : ME.
a
=
F
JE (1)
On utilise le repère de Frenet : soit
n
vecteur unitaire normal à la trajectoire et
t
vecteur
unitaire tangent à la trajectoire.
a
=
N
a
+
T
a
= aN.
n
+ aT.
t
; aN =
d
v2
et aT =
dt
dv
F
JE = FJE .
n
. D'après la relation (1) , on a : ME.
d
v2
=
d
M.M
G2
J
E
(2) et ME.
dt
dv
=0 (3)
On a donc
dt
dv
= 0, la vitesse est donc constante, le mouvement est uniforme.
c)
F
JE =
EJ
2
J
Eu
d
M.M
G
où
EJ
u
est un vecteur unitaire de
direction EJ, orienté de J vers E.
Les vecteurs vitesses
V
1 et
V
2 ont même norme, v1 = v2
mais leur direction est différente, tangente à la
trajectoire.
D'après la relation (1), a1 = a2 =
E
EJ
M
F
Elles ont donc même norme mais des directions
différentes.

CLASSE DE TERMINALE D.T.L. de PHYSIQUE-CHIMIE N°4
P.E. BONNEAU ANNEE 2004-2005 Page 3/4
II ) 1) D'après la relation (2) , on a :
r
vME2 .
= G.
2
.
r
MM J
E
=> v2 = G.
r
MJ
2) En une période T de révolution, le satellite parcourt une distance D égale au périmètre du
cercle de trajectoire.
Périmètre D = 2  r et v =
T
D
v2 =
2
2
).2(
T
r
= G.
r
MJ
=>
J
MG
r
..4 32
= T2 => T = 2
J
3
M.G
r
3) a) D'après ce qui précède :
3
2
r
T
=
J
MG.
42
. D'après cette relation, on constate que le rapport
3
2
r
T
ne dépend que de MJ, il est donc identique pour les 4 satellites.
b) La période de révolution de Io autour de Jupiter est TIo = 1 j 18 h 18 min.
Thébé autre satellite de Jupiter possède une orbite de rayon moitié de celui de l’orbite de
Io.
rTh / rIo = 1/2 , TIo2 / rIo3 = TTh2 / rTh3
=> TTh = TIo .
3
Io
3
Th
r
r
= ( 1 x 24 x 60 + 18 x 60 + 18 ) x
3
2
1
= 897 min = 14 h 57 min
4) Europe n'est pas « jupitostationnaire » car sa période est différente de la période de
révolution de Jupiter sur elle-même.
EXERCICE III - LE GRAND SAUT (4 points) [Tronc commun]
Partie A :
P = m.g = 1,6.103 x 9,8 = 1,57.104 N
PA = mair.g = mair.Vb.g = 1234.10-3 x 4,0.103 x 9,8 = 4,84.104 N
PA > P ; grâce à la poussée d'Archimède de l'air, le ballon peut s'élever facilement du sol.
Partie B :
1) Dans la première partie du saut, la vitesse est assez faible. D'après la pression de l'air et
sa masse volumique, la quantité d'air est faible, les frottements de l'air sont donc faibles,
d'autant qu'à ce stade du saut, le corps du parachutiste est aérodynamique.
On peut donc négliger l'action de l'air sur le parachutiste, il n'est donc soumis qu'à son poids,
il est donc en chute libre.
2) On étudie le système ( parachutisme + équipement) dans le référentiel terrestre galiléen
auquel on associe un repère (O,
i
) (
i
vecteur normé vertical vers le bas et O , point de
départ du saut )
On applique la 2ème loi de Newton :
ext
F 
= m.
a
=>
P
= m.
a
=>
g
=
a
=> g.
i
= a.
i
=> a = g
a =
dt
dv
= g => v = g.t + k ( k constante) ; à t = 0 s, v = k = v0 = 0 => v = g.t
v =
dt
dx
= g.t => x = ½ g.t2 + k' ( k' constante) ; à t = 0 s , x = k' = 0 => x = ½ g.t2

CLASSE DE TERMINALE D.T.L. de PHYSIQUE-CHIMIE N°4
P.E. BONNEAU ANNEE 2004-2005 Page 4/4
a) t1=vson/g=( 1067.103/3600)/9,7  30,6 => t1  31 s. Cela correspond à la valeur de l'énoncé.
b) x1 = ½ g.t12 = ½ 9,7 x 30,6 2 » 4 530 m. h1 = h – x1 = 40 000 – 4530  35 500 m
c) Ces valeurs correspondent à peu près à celles indiquées dans le document p9.
Partie C : Chute dans la basse atmosphère (troposphère) :
1) k = F /v2 ; [F] = [m.a] = M.(L.T-2 )
[k] = [F] / [v]2 = [m.a] / [v]2 = M.( L.T-2 ) / (L.T-1)2 = M.L-1 ; k se mesure en kg.m-1
2) Dans les conditions citées, on peut négliger la poussée d'Archimède de l'air raréfié.
Les forces s'exerçant sur le système sont : son poids
P
et la force de frottement de l'air
f
.
On étudie le système (parachutisme+équipement) dans le référentiel terrestre galiléen auquel
on associe un repère (O,
i
) (
i
vecteur normé vertical vers le bas et O, point de départ du
saut).
On applique la 2ème loi de Newton :
ext
F 
= m.
a
=>
P
+
f
= m.
a
=> m.g.
i
- k.v2.
i
= a.
i
=> a =
dt
dv
= g –
m
k
.v2 =>
dt
dv
= g –
m
k
.v2
3) a) La méthode d'Euler consiste à assimiler l'accélération a =
dt
dv
à
t
v
sur un intervalle de
temps t très court.
v = an .t => vn+1 = vn + an .t ; an = g –
m
k
.vn2
vn+1 = vn + (g -
m
k
).vn2.t = vn + g. t – k.
m
t
.vn2 = vn + A – B.vn2
A = g.t = 9,8 x 0,5 = 4,9 et B =
m
t
= 0,78 x
200
5,0
= 1,95.10-3
[A] = [vn] , A a donc la dimension d'une vitesse et se mesure en m.s-1
[vn+1] = [B].[vn]2 => [B] = [v] / [v]2 = 1 / [v] = T.L-1 . B se mesure en s.m-1
b) D'après le graphe (figure 1), il faut environ 10s pour atteindre la vitesse limite et
vlimite=50m.s-1 = 180 km.h-1
Cette valeur correspond à celle indiquée sur le film.