Leçon fractions 4e

Leçon N°7 : Le parallélogramme
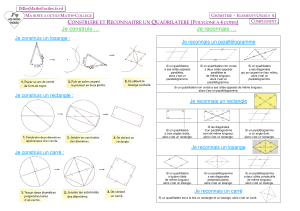
(1) Définition: Un parallélogramme est un quadrilatère ayant ses côtés opposés parallèles
(ou ayant ses côtés parallèles deux à deux).
(2) Quatre propriétés caractérisant le parallélogramme:
a) Un quadrilatère est un parallélogramme quand ses côtés opposés ont la même longueur.
(C’est la propriété utilisée pour construire au compas un parallélogramme dont on connaît trois sommets)
b) Un quadrilatère est un parallélogramme quand il a un centre de symétrie, c'est à dire quand ses
diagonales se coupent en leurs milieux (quand ses diagonales ont le même milieu).
c) Un quadrilatère est un parallélogramme quand il a deux côtés à la fois parallèles et de la même longueur
(C’est la propriété utilisée pour tracer un parallélogramme sur du papier quadrillé)
d) Un quadrilatère est un parallélogramme quand ses angles opposés ont la même mesure.
(3) Parallélogrammes particuliers:
a) Le rectangle
Définition: Un rectangle est un quadrilatère ayant quatre angles droits.
(Si trois des angles sont droits alors le quatrième l'est aussi)
Caractérisations du rectangle à partir du parallélogramme:
• Un parallélogramme est un rectangle quand il a un angle droit (ou deux côtés perpendiculaires).
• Un parallélogramme est un rectangle quand ses diagonales ont la même longueur.
b) Le losange
Définition: Un losange est un quadrilatère ayant ses quatre côtés de la même longueur.
Caractérisations du losange à partir du parallélogramme:
• Un parallélogramme est un losange quand il a deux côtés consécutifs de la même longueur.
• Un parallélogramme est un losange quand ses diagonales sont perpendiculaires.
c) Le carré
Définition: Un carré est un quadrilatère ayant quatre angles droits et quatre côtés de la même longueur.
Caractérisation du carré à partir du parallélogramme:
Un parallélogramme est un carré quand c'est à la fois un rectangle et un losange.
(4) Aire d’un parallélogramme
AB
C
D
H
K
Aire de ABCD = AB × AH
= AD × AK
= base × hauteur associée

AA
AA
AB
BB
B
B
C
C
C
C
CD
D
DD
D
(1) (2a) (2b)
(2c) (2d)
O
EEE FFF
G
GGH
HH
III
J
J
J
KKK
L
L
LO
(3b)(3b) (3b)
(3a) (3a) (3a)
(3c)