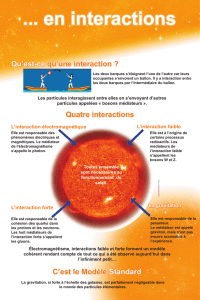
quantique particules -"l électron" -font -chapitre

UL7 - MODULE DE LECTURE D ’OUVRAGE
«QUANTIQUE -RUDIMENTS »
Jean-Marc LEVY-LEBLOND
Françoise BALIBAR
COMPORTEMENT COLLECTIF
QUANTONS IDENTIQUES
RIVIERE Nicolas -97085608
Licence de Physique 2000 -Université Paul Sabatier Toulouse III

SOMMAIRE
Principe de factorisation composée
Énoncé
Limite de validité
Théorie classique
Description collective des systèmes composés
Grandeurs collectives
Conclusion
Particules de Bose
Présentation
États à deux bosons
Propriété des bosons
États à n particules
Conclusion

Électron état initial p(1) état final r(1)
Photon état initial q(2)état final s(2)
Couple ( p(1) , q(2) )( r(1) , s(2) )
Amplitude de probabilité < r(1) , s(2) | p(1) , q(2) >
Probabilité P(1,2) = | < r(1) , s(2) | p(1) , q(2) > |2
Évènements indépendants P(1) = | < r(1) | p(1) > |2
P(2) = | < s(2) | q(2) > |2
⇒P(1,2) = P(1) . P(2)
Principe de factorisation composée
Énoncé
Principe de factorisation composée
< r(1) , s(2) | p(1) , q(2) > = < r(1) | p(1) > . < s(2) | q(2) >

Principe fondamental de le théorie quantique :
Indiscernabilité entre deux quantons
≠
Possibilité d’étiquetage par charge
Particules identiques
identique = indiscernabilité
Principe de factorisation composée
Limite de validité
Photon Photon
Électron Électron

- Possibilité de localisation
-Quantons dénombrés et individualisés
En physique quantique : particules dénombrées et non individualisées
Principe de factorisation composée
Théorie classique
- Quantons = particules classiques dénombrables, individualisées
= champs classiques indénombrables, non individualisés
-Systèmes composés = propriétés collectives
Conclusion