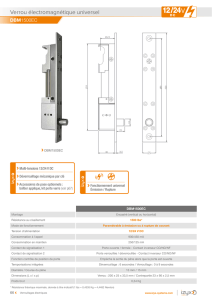
Électronique numérique Année 2011-2012

TEXTE DES TRAVAUX PRATIQUES
Électronique numérique
Année 2011-2012
Laboratoire SIGMA : Bât. H, 4ème étage
Travaux pratiques d’électronique : Bât. A, 1er étage

Travaux Pratiques d’Électronique, ESPCI 1ère année
1/21
PARTIE I : DE LA MÉMOIRE RS À LA BASCULE JK
Le but de ces travaux pratiques est d’introduire les notions nécessaires à l’étude et à
la réalisation des systèmes séquentiels.
I Définitions
Un système combinatoire est caractérisé par des relations booléennes entre ses n
entrées (ei) et ses m sorties (Sj). La valeur du vecteur S est entièrement déterminée
par celle du vecteur d’entrée e, c’est une fonction de e (voir Figure 1).
Figure 1. Représentation d’un système combinatoire
Ceci n’est plus vrai dans le cas d’un système séquentiel, pour lequel à une même
valeur du vecteur d’entrée peuvent correspondre différentes valeurs du vecteur de
sortie. Plus précisément, c’est à une séquence temporelle déterminée des valeurs du
vecteur d’entrée que correspond une séquence du vecteur de sortie. Cette définition
suggère l’existence de mémoires dans les systèmes séquentiels. Le temps joue un
rôle fonctionnel.
Un système séquentiel se représente par un modèle bouclé, comportant des entrées
indépendantes, des sorties, des variables d’état (ou excitations) qui sont rebouclées
et retardées pour constituer des entrées d’état. Les sorties et les excitations sont des
fonctions booléennes des entrées indépendantes et d’état (voir Figure 2).
Figure 2. Représentation d’état d’un système séquentiel
Travaux Pratiques d’Électronique, ESPCI 1ère année
2/21
II La mémoire RS
C’est une mémoire très simple : il faut 4 transistors. Elle est représentée sur la
Figure 3, dans une réalisation avec des portes NON-ET (une autre réalisation utilise
des portes NON-OU).
Figure 3. La mémoire RS (réalisation avec des portes NON-ET).
Les sorties Q et P ne peuvent pas s’exprimer comme des fonctions booléennes des
seules entrées a et b à cause du bouclage. Pour analyser le fonctionnement de ce
système séquentiel, il est nécessaire de prendre en considération le temps de
traversée des portes. Pour définir les excitations, il faut supprimer toutes les boucles
en coupant le minimum de connexions (une coupure = une excitation). Il suffit ici de
couper une seule connexion pour obtenir une telle représentation, comme le montre
la Figure 4.
Figure 4. Modèle pour l’analyse de la mémoire RS (système séquentiel).
Le système combinatoire ci-dessus fournit les fonctions booléennes de l’excitation et
des sorties :
Q=a.b.q =a+b.q
P=q.b =q+b
!
"
#
$
#
On en déduit les tables de vérité de l’excitation et des sorties (Figure 5).

Travaux Pratiques d’Électronique, ESPCI 1ère année
3/21
q
Q
a b
0 0
0 1
1 1
1 0
0
1
1
1
0
1
1
0
0
1
q
Q P
a b
0 0
0 1
1 1
1 0
0
1
1 1
1 1
0 1
1 0
1 0
0 1
0 1
1 1
(a)
(b)
Figure 5. Tables de vérité de l’excitation (a) et des sorties (b) de la mémoire RS.
Chaque colonne correspond à une combinaison des entrées primaires. Agir sur le
système consiste à changer de colonne. Par hypothèse, on ne change qu’une entrée
primaire à la fois. Un état pour lequel Q = q est dit stable, sinon il est dit instable. Sur
la Figure 5, les états stables sont entourés d’un cercle. Étudier les transitions entre
les états stables.
Le chronogramme suivant des entrées a et b illustre une utilisation typique de cette
mémoire.
a
b
Q
P
Figure 6. Chronogramme d’utilisation typique de la mémoire RS.
Tracer les chronogrammes de Q et de P. Décrire le fonctionnement de la mémoire,
en particulier la fonction des entrées a et b, et en déduire quelle est l’entrée s
(comme « set » : mise à 1 de la sortie Q) et l’entrée r (comme « reset » : mise à 0 de
la sortie Q).
Utilisation de la mémoire RS
Du point de vue de l’utilisateur, il est intéressant de disposer de la sortie Q et de son
complément
Q
. La table de vérité des sorties montre que P =
Q
pour tous les états
stables sauf pour les entrées a = b = 0. Il suffira donc d’interdire cette combinaison
des entrées. Montrer que c’est le cas pour l’application la plus connue, un dispositif
de suppression des commutations intempestives dues aux rebonds des interrupteurs
mécaniques utilisés comme éléments de commande des systèmes logiques, dit
dispositif « anti-rebond », représenté sur la Figure 7.
Travaux Pratiques d’Électronique, ESPCI 1ère année
4/21
Figure 7. Dispositif antirebond.
Manipulation
Réaliser une mémoire RS à l’aide de deux circuits logiques NON-ET à deux entrées
(circuit 7400 ; vérifier individuellement le bon fonctionnement de toutes ses portes au
préalable). Prévoir d’utiliser quatre circuits comme indiqué en Annexe 1.
Figure 8. Chronogramme de test.
Vérifier les états stables et les transitions données par la table d’excitation en
appliquant la séquence de la Figure 8 aux entrées à l’aide d’interrupteurs (compléter
la séquence de Q).
III Le verrou RS
C’est la mémoire verrouillable la plus simple que l’on puisse imaginer : elle ne
comporte elle aussi qu’une excitation, voir Figure 9. L’entrée de verrouillage est
notée v.

Travaux Pratiques d’Électronique, ESPCI 1ère année
5/21
Figure 9. Le verrou RS.
q
Q P
s r
0 0
0 1
1 1
1 0
0
1
0 1
1 0
1 0
0 1
1 1
v
0
1
0 1
0 1
0 0
0 1
1 1
1 0
1 1
0 1
0 1
1 0
1 0
1 0
0 1
1 1
1 0
Figure 10. Table de vérité des sorties du verrou RS.
La table de vérité des sorties du verrou RS est représentée sur la Figure 10. Étudier
le fonctionnement du verrou à l’aide de cette table. En particulier :
a) Expliciter son comportement lorsque v = 0 et qu’interviennent des transitions sur
les entrées s et r. De même lorsque v = 1.
b) Établir quelle transition de l’entrée de verrouillage provoque la transition éventuelle
des sorties.
c) Montrer que si v passe de 1 à 0 avec s = r = 1, la valeur de Q résultante n’est pas
prévisible (les temps de traversée des deux couples de portes NON-ET sont
différents et inconnus) : nous dirons que le fonctionnement de la verrou comporte un
aléa de propagation1.
Utilisation du verrou RS ; verrou D
Ceci impose donc d’interdire la combinaison s = r = 1 lorsque l’on utilise ce verrou.
Voici un chronogramme d’utilisation typique :
1 Noter que la table de la Figure 10 ne met pas en évidence l’aléa de propagation, observation qui
dévoile une carence de notre méthode d’analyse : la table de vérité des excitations ne permet pas
d’analyser complètement le fonctionnement d’un système séquentiel, à une seule excitation qui plus
est ! En effet, dans un circuit où un même signal emprunte deux chemins symétriques, il faut, pour
mettre en évidence un aléa de propagation, considérer deux signaux différents, un par chemin, pour
établir la table d’excitation. À faire en exercice, pour le schéma simplifié avec s = r = 1 = cte, qui est le
cas qui nous occupe, avec deux signaux v1 et v2 pour le signal v.
Travaux Pratiques d’Électronique, ESPCI 1ère année
6/21
v
s
r
Q
déverrouillage
déverrouillage
verrouillage
Figure 11. Chronogramme d’utilisation du verrou RS.
En général, le verrou RS est utilisé pour constituer un « verrou D ». Il suffit pour cela
de réaliser s = d et r =
d
. Les entrées s et r ne sont donc jamais à r = s = 1. Le
problème dû à l’aléa de propagation n’existe donc pas pour le verrou D2. De plus,
pour tous les états stables, on a P =
Q
, comme le montre la table de vérité des
sorties ci-dessous.
q
Q P
d
0
1
0
1
0
1
1 1
0 1
0 1
v
0
1
0 1
0 1
1 0
1 0
1 0
d
s
r
Q
P
v
verrou D
verrou
SR
Figure 12. Le verrou D.
Le chronogramme de la Figure 13 illustre le fonctionnement typique du verrou D.
Lorsque v = 1, Q suit l’entrée d avec un retard de quelques nanosecondes. La
transition 1 ! 0 de l’entrée v verrouille la sortie Q à la valeur qu’elle possède à cet
instant.
v
d
Q
Figure 13. Chronogramme d’utilisation du verrou D.
2 En fait, à cause du retard introduit par la porte NON entre les deux entrées s et r, les entrées s et r
sont à 1 pendant quelques nanosecondes quand d passe de 0 à 1. Pour qu’il y ait un aléa de
propagation, il faut que le verrou passe de 0 à 1 justement pendant ces quelques nanosecondes.
Évaluer la probabilité d’un tel événement.

Travaux Pratiques d’Électronique, ESPCI 1ère année
7/21
Néanmoins, comme le verrou RS, le verrou D ne peut être utilisé comme élément de
base d’un système de logique synchrone dont l’horloge serait appliquée à l’entrée v.
Exercice : montrer que l’on ne peut pas réaliser un N-registre à décalage avec N
verrous D en cascade.
Manipulation
Réaliser un verrou RS en utilisant la mémoire RS précédente, sur le même circuit
7400.
IV La bascule RS
Les éléments de base des systèmes synchrones sont des bascules dont,
contrairement aux verrous, le signal d’horloge seul provoque les transitions de la
sortie en fonction des valeurs imposées aux entrées. Les problèmes apparus avec
les verrous sont résolus en compliquant la structure. Ainsi, les bascules possèdent
au moins deux excitations.
On obtient une bascule RS en mettant en cascade deux verrous RS, le verrou
« maître » étant commandé par l’horloge, et le verrou « esclave » par son
complément, voir Figure 14. Les deux excitations sont par exemple U et Q.
Figure 14. La bascule RS.
N.B. L’indétermination de la sortie des verrous lorsque s = r = 1 persiste ici et conduit
à interdire cette combinaison des entrées lors de l’utilisation de cette bascule.
La Figure 15 montre la table des excitations U et Q. Vérifier que les entrées s et r ne
provoquent jamais de transition de la sortie Q, et qu’elles sont provoquées par la
transition 1 ! 0 du signal h. Comme nous l’avons dit plus haut, c’est cette propriété
qui définit ce que nous appelons une bascule et ce qui en fait un élément de base
fiable d’un système synchrone.
Travaux Pratiques d’Électronique, ESPCI 1ère année
8/21
uq
U Q
s r
0 0
0 1
1 1
1 0
0 0
0 0
0 0
1 0
h
0
1
0 0
0 0
0 0
0 1
1 1
1 0
1 0
0 0
0 0
0 1
0 1
1 1
1 1
1 1
1 1
0 1
1 0
0 0
1 0
0 1
1 1
1 0
1 1
1 1
1 1
1 1
1 1
1 1
1 1
1 1
0 0
0 0
0 0
0 0
1 1
1 0
Figure 15. Table de vérité des excitations de la bascule RS.
Utilisation de la bascule RS
Montrer que, contrairement au verrou RS, une bascule RS maître-esclave peut-être
utilisée comme élément de base d’un registre à décalage (voir le schéma du registre
à décalage SN7495 sur le site de Texas Instruments http://www.ti.com/).
Manipulation
Réaliser une bascule RS en utilisant le verrou RS précédent comme verrou esclave.
Prendre des NON-ET à 3 entrées pour les entrées du verrou maître (circuit
7410), et des NON-ET à 2 entrées pour ses sorties (cf. Annexe 1). Mettre les
entrées inutiles au +5V (ce qui revient à imposer un « 1 » logique), elles seront
utilisées pour le montage suivant. Tester le verrou maître seul, puis mettre ses
sorties en entrée du verrou esclave, ainsi que l’horloge complémentée (circuit 7404).
Vérifier le bon fonctionnement de la bascule.
V La bascule JK créneau
Une légère modification de la bascule RS permet d’obtenir une bascule sans aléa de
propagation, et qui permet d’utiliser la combinaison j = k = 1 conduisant au
changement inconditionnel de la valeur de la sortie. Le fonctionnement d’une telle
bascule est défini par la pseudo-table de vérité (voir Annexe) du Tableau 1 :