ALI et électrostatique

Colles semaine 15, sujet A Langevin–Wallon, PT 2016-2017
ALI et électrostatique
Question de cours
Calculer le champ électrostatique créé par un plan chargé en surface avec une densité de charge uniforme σ0.
Exercice 1 : Simulateur d’inductance
i
u
−RN
i3
R
i1
i2
R
C
−
+
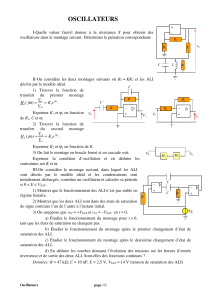
Les bobines sont des composants très utilisés en électronique de puis-
sance, mais leur grande taille les rend peu pratiques à insérer dans
des circuits intégrés. Ce n’est cependant pas un souci puisqu’elles
peuvent être remplacées par des montages à ALI comme celui re-
présenté ci-contre, beaucoup plus compact.
L’ALI est supposé idéal et fonctionnant en régime linéaire : on peut
donc supposer le régime sinusoïdal forcé sans perte de généralité.
Le dipôle « −RN» désigne l’impédance d’entrée d’un autre mon-
tage à ALI, dit à résistance négative, qui a exactement le même
comportement qu’une résistance −RN<0.
Déterminer l’impédance d’entrée Z=U/I du montage. En déduire
la valeur à donner à RNpour obtenir une inductance pure.
Éléments de correction de l’exercice 1 :
Loi des nœuds :
I=I1+I2+I3
Lois de comportement :
I3=−U
RN
et I2=U
R
car V+=V−= 0. Calculer I1demande une loi des mailles en plus,
I1=U−VS
Ravec VS=−1 jCω I2
la tension de sortie de l’ALI. Ainsi,
I=2U
R−S R−U RN
=2U
R+1 jRCω I2−U RN
et donc
I=2
R+1 jR2Cω −1 RNU
Pour une bobine idéale, on doit avoir
I=1
jLω U .
On a donc équivalence si RN=R/2, sinon le montage est équivalent à une bobine idéale montée en parallèle d’une
résistance telle que 1/r = 2/R −1/RN.
1/5 Étienne Thibierge, 19 janvier 2017, www.etienne-thibierge.fr

Colles semaine 15, sujet A : ALI et électrostatique Langevin–Wallon, PT 2016-2017
2/5 Étienne Thibierge, 19 janvier 2017, www.etienne-thibierge.fr

Colles semaine 15, sujet B Langevin–Wallon, PT 2016-2017
ALI et électrostatique
Question de cours
Calculer le champ électrostatique créé par un cylindre chargé en volume avec une densité de charge uniforme ρ0.
Exercice 1 : Oscillateur à résistance négative
RN
R
RiR
i−
+
C
L
R0
u
On s’intéresse dans un premier temps au montage à ALI encadré sur
le schéma ci-contre, appelé montage à résistance négative. L’ALI est
considéré comme idéal.
1 - Justifier que l’ALI peut fonctionner en régime linéaire. On admet
ce fonctionnement par la suite.
2 - Déterminer l’impédance d’entrée Z=u/i du montage. Justifier
sa dénomination de « résistance négative ».
3 - Exprimer en fonction de ile courant iR. D’où provient la diffé-
rence et comment est-elle compensée ?
On considère maintenant le montage dans son ensemble.
4 - Établir l’équation différentielle vérifiée par i. Discuter les différentes solutions de cette équation et leur stabilité.
Comment évolue l’amplitude des oscillations au cours du temps?
Éléments de correction de l’exercice 1 :
1Double bouclage sur +et −donc fonctionnement linéaire possible mais pas certain.
2Potentiel de sortie de l’ALI exprimé à partir de la boucle de rétroaction négative :
vs=u−RNi
Potentiel de sortie de l’ALI avec la rétroaction positive : les deux résistances Rforment un pont diviseur de tension,
on peut donc introduire dans le calcul v+=v−=u, soit
v+
vs
=R
R+Rsoit vs= 2v+= 2u
Et finalement
u−RNi= 2usoit u=−RNi
Comme l’impédance d’entrée est orientée en convention récepteur, on a bien équivalence avec une loi d’Ohm d’une
résistance négative.
3ALI idéal donc i−=i+= 0. Loi d’Ohm sur la résistance RN:
u−vs=RNi=RiRd’où iR=RN
Ri .
Différence provient du courant de sortie de l’ALI, qui est inconnu a priori (et qui n’a aucune raison d’être tout le
temps nul, et ne peut même jamais l’être dans le montage). Comme le courant de sortie du montage à résistance
négative est également i(évident vu le circuit complet), on en déduit qu’une partie du courant part dans le fil
connecté à la masse. C’est une remarque très générale : le fait de placer la masse à un endroit du circuit a un effet sur
les tensions, mais aussi sur les intensités, la masse peut toujours « faire disparaître » ou « créer » un courant qu’on
ne peut pas connaître a priori, et qui n’a aucune raison d’être nul.
4Loi des mailles en convention récepteur pour tout le monde :
u+uC+uL+u0= 0
3/5 Étienne Thibierge, 19 janvier 2017, www.etienne-thibierge.fr

Colles semaine 15, sujet B : ALI et électrostatique Langevin–Wallon, PT 2016-2017
Tout le monde est parcouru par le même courant i, donc les lois de comportement donnent :
−RNi+uC+Ldi
dt+R0i= 0
Il faut dériver pour utiliser la loi de comportement du condensateur :
−RN
di
dt+i C+Ld2i dt2+R0
di
dt= 0
Soit en ordonnant les dérivées :
Ld2i
dt2+ (R0−RN)di dt+1 Ci= 0
Discussion de stabilité des solutions en fonction du signe de R0−RN. Dans le cas instable l’amplitude des oscillations
finit par saturer lorsque vs=±Vsat, et l’équation différentielle obtenue n’est plus valable car l’ALI passe en régime
saturé. Le montage change donc de comportement.
4/5 Étienne Thibierge, 19 janvier 2017, www.etienne-thibierge.fr

Colles semaine 15, sujet C Langevin–Wallon, PT 2016-2017
ALI et électrostatique
Question de cours
Calculer le champ électrostatique créé par une boule chargée en volume avec une densité de charge uniforme ρ0.
Exercice 1 : Oscillateur à ALI
R1
+
C3
R3
−
R2
v1
v3
vs
ε
Dans le montage ci-contre, l’ALI fonctionne en régime saturé. On note ε=
v+−v−la tension différentielle à l’entrée de l’ALI. On suppose qu’à t= 0 ,
le condensateur C3est déchargé et ε > 0. On pose
α=R1
R1+R2
et τ=R3C3
Données : R1= 19,6 kΩ,R2= 40,2 kΩ,R3= 100 kΩ,C3= 471 pF,Vsat =
15 V.
1 - Exprimer v3(t)pour t > 0et tant que l’état de saturation de l’ALI reste le même. En déduire qu’il existe t1tel
que l’ALI bascule en saturation basse. Déterminer t1en fonction de τet α.
2 - Montrer qu’il existe t2> t1tel que l’ALI bascule en saturation haute. Déterminer t2−t1en fonction de τet α.
3 - Montrer que vs(t)et v3(t)sont des signaux périodiques, dont on note la période T.
4 - Tracer l’allure des variations de vs(t)en fonction de v3(t). Indiquer sur le graphe son sens de parcours.
5 - Montrer que la période Tpeut s’écrire
T= 2τln 1 + α
1−α.
La calculer numériquement ainsi que la fréquence correspondante.
Éléments de correction de l’exercice 1 :
Voir le site de François-Xavier Coq, http://www.lycee-pothier.com/LYCEE/psi/file/physique/exercices/
TraitSignal_Oscillateurs/OSCILL26.pdf
5/5 Étienne Thibierge, 19 janvier 2017, www.etienne-thibierge.fr