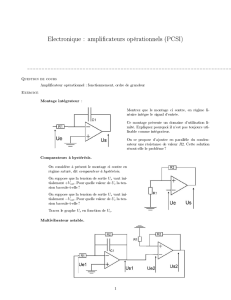
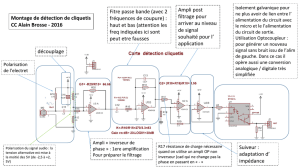
amplificateur opérationnel - Math Plp

•
•ω
•

Z N
R C C C
0 5 10 15

µA702 µA709 µA741
T3T4
T1T2
−Vee
T T
T T
1 2
3 4
Out
Out
+Vcc
+Vcc
−Vee
I−
I+I+
I− −
+

µA741 TL081
18
7
6
5
4
3
2
Offset
In −
In +
− Vee Offset
+ Vcc
Out
4,7 kΩ
4,7 kΩ
4,7 kΩ
4,7 kΩ
+
+Vcc
V
−Vee
−
9 V Out
y
x
In
In
A
B
C
x y
VI+<VI−x↔A y ↔B VO' −Vee
VI−<VI+x↔B y ↔A VO'+Vcc
VI−= VOx↔C y ↔A VO= VI+
VI−= VOx↔C y ↔B VO= VI+
VI−= VI+x↔A y ↔A
−Vee +Vcc

+Vcc
Out
−Vee
−
+
0 ref
RR1 2
In
0 ref
u
t
V In V Out
O l
O h +Vcc
−Vee
T h
T l
O l
O h +Vcc
−Vee
+Vcc u
u
−Vee
T l T h
fR2\ {(x, y), x =y}R
f(x, y) = +∞x < y
f(x, y) = −∞ y < x
f{(x, y), x =y}Vi−= Vi+V o
Vo