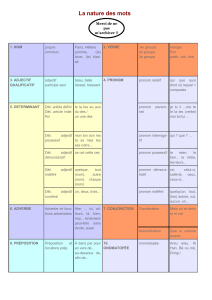
n − 1 et notons Δ ij = (−1)i+jdét(A − Li − Cj). On appelle Δij - IMJ-PRG

6.2. CAS G´ EN´ ERAL 59
n−1et notons Δij = (−1)i+jdét(A−Li−Cj). On appelle Δij le cofacteur
d’indice i, j de A. Par exemple, si A=
1 2 3
4 5 6
7 8 9
, alors A−L2−C3=1 2
7 8.
Et Δ23 = (−1)2+3 
1 2
7 8
=−(8 −14) = 6.
On ´enonce maintenant le th´eor`eme g´en´eral sur le d´eterminant, qui permet
de le d´efinir par r´ecurrence sur la dimension :
Th´eor`eme 6.2.2. — Soit n∈N∗. Il existe une unique application, appel´ee
le d´eterminant et not´ee dét, de Mn(K)dans Kmultilin´eaire et altern´ee telle
que dét(In) = 1. De plus toute fonction Dmultilin´eaire est altern´ee v´erifie
D(A) = D(In)dét(A).
Enfin, on a les formules suivantes.
–D´eveloppement du d´eterminant selon la ligne i:(QC)
dét(A) =
n
j=1
aij Δij .
–D´eveloppement du d´eterminant selon la colonne j:
dét(A) =
n
i=1
aij Δij .
On notera parfois |A|le d´eterminant de A.
On renvoie `a la section annexe de ce chapitre (non trait´ee en amphi – `a la
fin du chapitre) pour la preuve g´en´erale. Nous traitons dans la section suivante
le cas des matrices de taille 3, qui contient les id´ees essentielles
6.2.1. Cas des matrices de taille 3. — Dans cette section, on consid`ere
une fonction Dde M3(K)dans Kqui est multilin´eaire et altern´ee et telle que
D(I3)=1. On va montrer qu’il n’y a qu’une seule possibilit´e, qu’on appelera
le d´eterminant. Cette section sert aussi d’exemple pour les notions abstraites
(multilin´earit´e, cofacteurs...) d´efinies ci-dessus.
Soit donc A=
a11 a12 a13
a21 a22 a23
a31 a32 a33
. On veut montrer qu’on n’a pas le choix
pour d´eterminer D(A). On commence par utiliser la lin´earit´e par rapport `a la
premi`ere colonne.

60 CHAPITRE 6. D´ ETERMINANTS
Notons C1=
a11
a21
a31
=a11 
1
0
0
+a21 
0
1
0
+a31 
0
0
1
. La lin´earit´e de Dpar
rapport `a la premi`ere colonne permet d’´ecrire :
D(A) = a11D
1a12 a13
0a22 a23
0a32 a33
+a21D
0a12 a13
1a22 a23
0a32 a33
+a31D
0a12 a13
0a22 a23
1a32 a33
´
Etudions le premier de ces termes : D
1a12 a13
0a22 a23
0a32 a33
. On peut maintenant
d´ecomposer la deuxi`eme colonne en somme :
C2=a12 
1
0
0
+a22 
0
1
0
+a32 
0
0
1
.
En utilisant la lin´earit´e par rapport `a cette colonne, on arrive `a :
D
1a12 a13
0a22 a23
0a32 a33
=a12D
1 1 a13
0 0 a23
0 0 a33
+a22D
1 0 a13
0 1 a23
0 0 a33
+a31D
1 0 a13
0 0 a23
0 1 a33
Mais, dans le premier de ces termes, les deux premi`eres colonnes sont ´egales,
donc on peut utiliser la propri´et´e d’alternance : D
1 1 a13
0 0 a23
0 0 a33
= 0.
On a donc D
1a12 a13
0a22 a23
0a32 a33
=a22D
1 0 a13
0 1 a23
0 0 a33
+a31D
1 0 a13
0 0 a23
0 1 a33
.En
utilisant la lin´earit´e par rapport `a la troisi`eme colonne et l’alternance quand
deux colonnes sont ´egales, on obtient successivement :
D
1 0 a13
0 1 a23
0 0 a33
=a13D
1 0 1
0 1 0
0 0 0
+a23D
100
011
000
+a33D
100
010
001
=a33D
1 0 0
0 1 0
0 0 1
et

6.2. CAS G´ EN´ ERAL 61
D
1 0 a13
0 0 a23
0 1 a33
=a13D
101
000
010
+a23D
100
001
010
+a33D
100
000
011
=a23D
100
001
010
On a donc r´eussi `a calculer le premier terme de la d´ecomposition de D(A):
a11D
1a12 a13
0a22 a23
0a32 a33
=a11a22a33D
100
010
001
+a11a32a23D
100
001
010
En raisonnant de mˆeme sur les 2 autres termes, on trouve :
D(A)=a11a22a33D
1 0 0
0 1 0
0 0 1
+a11a32a23D
100
001
010
+a21a12a33D
0 1 0
1 0 0
0 0 1
+a21a32a13D
001
100
010
+a31a12a23D
0 1 0
0 0 1
1 0 0
+a31a22a13D
001
010
100
On voit donc que Dne d´epend que de ses valeurs sur les 6matrices avec
des 0et des 1ci-dessus. Pour conclure, il suffit de comprendre ces 6valeurs.
Pour ¸ca, la propri´et´e g´en´erale suivante :
Proposition 6.2.3. — Soient D:Mn(K)→Kmultilin´eaire et altern´ee,
A∈Mn(K)et A�obtenue `a partir de Aen ´echangeant deux colonnes de A.
Alors on a D(A) = −D(A�).
D´emonstration. — Notons A= (C1| · · · |Ci| · · · |Cj| · · · |Cn)et
A�= (C1| · · · |Cj| · · · |Ci| · · · |Cn)(on a ´echang´e les colonnes iet j).
Consid´erons la matrice B= (C1| · · · |Ci+Cj| · · · |Ci+Cj| · · · |Cn). Elle a deux
colonnes ´egales, donc D(B)=0. Mais en utilisant la lin´earit´e par rapport `a la
colonne i, on a
D(B)=D(C1| · · · |Ci| · · · |Ci+Cj| · · · |Cn)+D(C1| · · · |Cj| · · · |Ci+Cj| · · · |Cn).

62 CHAPITRE 6. D´ ETERMINANTS
On utilise dans les deux termes ci-dessus la lin´earit´e par rapport `a la colonne
jpour obtenir :
D(B) = D(C1| · · · |Ci| · · · |Ci| · · · Cn)+D(C1| · · · |Ci| · · · |Cj| · · · Cn)
+D(C1· · · |Cj| · · · |Ci| · · · Cn)+D(C1· · · |Cj| · · · |Cj| · · · Cn)
= 0+D(A)+D(A�)+0
Les deux z´eros sont obtenus car deux colonnes des matrices correspondantes
sont ´egales.
Finalement D(A)+D(A�) = D(B) = 0, donc D(A) = −D(A�).
Revenons donc `a nos six matrices. On obtient :
D
100
001
010
=D
010
100
001
=D
001
010
100
=−D(I3)
car on peut passer de chacune de ces trois matrices `a I3en ´echangeant deux
colonnes.
En revanche D
0 1 0
0 0 1
1 0 0
=D
001
100
010
=D(I3)car il faut 2´echanges
pour revenir `a I3.
En se rappelant qu’on a suppos´e D(I3)=1on obtient bien l’unicit´e (et
donc nous revenons `a la notation dét) :
dét(A) = a11a22a33 −a11a32a23 −a21a12a33 +a21a32a13 +a31a12a23 −a31a22a13.
Cette formule s’appelle la formule de Sarrus. Attention `a son utilisation dans
les calculs, elle est souvent mal appliqu´ee.
On peut maintenant comprendre les formules de d´eveloppement suivant les
lignes ou les colonnes. Par exemple, pour la premi`ere colonne, on groupe les
termes :
dét(A) = a11(a22a33 −a32a23)−a21(a12a33 −a32a13)+a31(a12a23 −a22a13)
=a11dét a22 a23
a32 a33−a21dét a12 a13 a32 a33+a31dét a12 a13 a22 a23
On reconnait des cofacteurs, comme d´efinis au d´ebut de cette section : dét(A) =
a11Δ11(A)+a21Δ21(A)+a31Δ31(A).
En factorisant d’abord les termes de la premi`ere ligne, on trouve : dét(A) =
a11Δ11(A)+a12Δ12(A)+a13Δ13(A).

6.2. CAS G´ EN´ ERAL 63
6.2.2. Retour au cas g´en´eral : quelques propri´et´es du d´eterminant.
—
Proposition 6.2.4. — Si une matrice A=
a1
�a2
.
.
.......
�. . . �an
est triangu-
laire inf´erieure, alors dét(A) = a1. . . an.
D´emonstration. — On le prouve directement par r´ecurrence sur n: par d´efini-
tion du d´eterminant 
a1
�a2
.
.
.......
�... �an
=a1
a2
......
. . . �an
+ 0 = a1a2···an
On en tire du th´eor`emes les deux cons´equences suivantes :
Proposition 6.2.5. — Pour toutes matrices Aet Bdans Mn(K), on a (QC)
dét(AB) = dét(A)dét(B)et
dét(tA) = dét(A).
D´emonstration. — Fixons A∈Mn(K)et consid´erons la fonction Dd´efinie
par D(B) = dét(AB). Montrons qu’elle est multilin´eaire et altern´ee. Remar-
quons pour ¸ca que si B= (C1|...|Cn), alors AB = (AC1|...[ACn).
L’alternance est alors imm´ediate : si deux colonnes de Bsont ´egales, alors
deux colonnes de AB sont ´egales et donc (par alternance de dét), D(B) =
dét(AB)=0.
Pour la multilin´earit´e, fixons Vun vecteur colonne, 1≤j≤net α∈
K. Modifions la matrice B�en modifiant sa j-`eme colonne. Notons B�=
(C1|...|αCj+V|...|Cnet B�� = (C1|...|V|...|Cn). On veut ´ecrire : D(B�) =
αD(B)+D(B��). Remarquons que, par lin´earit´e de C→AC,ona:
AB�= (AC1|...|A(αCj+V)|...|Cn)=(AC1|...|αACj+AV )|...|Cn).
Donc, par multilin´earit´e de dét, on obtient la multilin´earit´e :
D(B�) = dét(AB�)
=αdét(AC1|...|ACj|...|ACn) + dét(AC1|...|AV |...|ACn)
=αdét(AB) + dét(AB�� )
=αD(B)+D(B��).