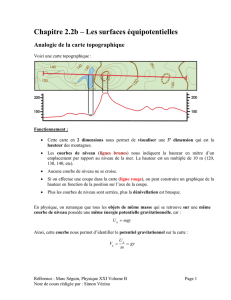
TP no 2 – Lignes de champ et équipotentielles

TP no2 – Lignes de champ et équipotentielles
PREPARATION (à rédiger avant de venir en TP)
Définitions
– La force électrique Fexercée sur une charge ponctuelle qpar le champ électrique E
s’écrit F=q E. Ce champ électrique Ecréé en un point (x,y,z) par une distribution de
charges quelconque est relié au potentiel Vpar la relation :
E=−
−−−→
gradV=−
∂V
∂x
ux−
∂V
∂y
uy−
∂V
∂z
uz
– Une ligne de champ est en tout point tangente au champ considéré. Elle donne la direc-
tion du champ. Les lignes de champ sont orientées des charges positives vers les charges
négatives. Elles respectent la symétrie de la distribution des charges et ne se croisent pas
(sauf là où le champ est nul ou non défini). Les équipotentielles sont les courbes de po-
tentiel constant. Les lignes de champ et les équipotentielles sont orthogonales.
– Quelque soit la forme d’un conducteur, sa surface est une équipotentielle V=cste. Le
champ électrique y est localement perpendiculaire à la surface. Dans un conducteur à
l’équilibre, le champ électrique est nul et le potentiel est constant. Toutes les charges
sont distribuées sur la surface du conducteur avec une densité surfacique de charge σ.
Condensateur plan On veut déterminer les lignes de champ et les équipotentielles d’un
condensateur plan. Soient deux plans conducteurs parallèles de même surface Set distants
de e, séparés par un milieu polarisable de permittivité diélectrique . L’un est porté au poten-
tiel de référence V=0 et l’autre au potentiel V=V0(Fig.5). On suppose que l’on peut négliger
les effets de bord, c’est-à-dire que des dimensions des armatures sont grandes par rapport à
leur espacement (limite du condensateur plan infini).
Rappel : La capacité Cde ce condensateur plan est donnée par C=S/elorsqu’on néglige
les effets de bord. La charge électrique portée par une armature est Q=CV où Vest la ddp
entre les armatures.
FIGURE 5 – Schéma en coupe du condensateur plan
1. Soit E=E(x,y,z) ule champ électrique général dans ce système. Trouvez les invariances
de ce système et déduisez-en que E(x,y,z) ne dépend plus que d’une variable. Trouvez les
propriétés de symétrie de ce système et déduisez-en la direction  udu champ électrique.
2. Dessinez alors la forme des lignes de champ et des équipotentielles.
3. σ=dQ/dS est la densité surfacique de charge. Pourquoi peut-on écrire σ=Q/Soù Qet
Ssont les charge et surface totales des armatures ?
4. Les mesures de potentiel que vous ferez en TP montrent que V(x)=kx où kest une
constante. Ecrivez Een fonction de k. Quelle est la dimension de k ?
9

5. En utilisant les conditions aux limites pour le potentiel sur les armatures, exprimez ken
fonction de V0. Montrez, à partir des expressions données précédemment, que le champ
électrique entre les armatures s’écrit E=−σ
ux
6. Comment calculer σà partir de la mesure expérimentale de k?
FIGURE 6 – Conducteur cylindrique entre deux plaques.
On ajoute entre les deux plans un conducteur cylindrique (Fig.6). Que se passe-t-il à l’in-
térieur du cylindre ? Que deviennent les équipotentielles et les lignes de champ ? Comment se
répartissent les charges sur le cylindre ? Ces questions appellent des réponses qualitatives.
Images électriques.
1. Calculez le champ et le potentiel électriques créés par deux fils conducteurs de longueur
L, parallèles et portant respectivement une charge +Qet −Qet séparés d’une distance d
(Fig. 7a). Lest suffisamment grand pour considérer les fils comme infinis et se ramener à
un problème à deux dimensions dans un plan perpendiculaire aux fils. On peut prendre
V=0 au plan médian.
2. Tracer l’allure des équipotentielles et des lignes de champ dans un plan perpendiculaire
aux fils.
+Q -Q
d
Vue en coupe
a)
+Q
d/2
b)
Plan
médian
Plan
métallisé
FIGURE 7 – Principe des images électriques
3. On remplace le deuxième fil par un plan infini conducteur relié au sol que l’on place sur
le plan médian (Fig. 7b). Comment sont modifiées les lignes de champ et les équipoten-
tielles ?
4. Pourquoi appelle-t-on cette manière de calculer le champ créé par des charges et des
surfaces métallisées la méthode des images électriques ? Quel est l’intérêt de cette mé-
thode ?
10

TRAVAIL EXPERIMENTAL
La cuve rhéographique. Une cuve est remplie sur une faible épaisseur d’un liquide conduc-
teur de résistivité suffisamment élevée (l’eau du robinet) pour que le courant reste faible. Cette
eau permettra la mesure des ddp avec le voltmètre. On impose la valeur du potentiel dans
des régions bien déterminées par des électrodes métalliques reliées à un générateur. On peut
montrer que la distribution résultante des potentiels dans le milieu conducteur (électrolyte) est
identique à la distribution des potentiels électrostatiques dans le vide pour les mêmes condi-
tions aux limites. Il suffit alors de déterminer point par point, à l’aide d’une sonde reliée à un
voltmètre, la valeur du potentiel dans le liquide et construire ainsi la carte des équipotentielles
dans le plan de la cuve. On peut alors en déduire les lignes de champ électrique pour la confi-
guration choisie.
1. – Condensateur plan
Dans une cuve rectangulaire partiellement remplie d’eau, on dispose deux électrodes mé-
talliques planes E1et E2entre lesquelles on crée une ddp. Pour minimiser les effets secondaires
liés à l’électrolyse, elles sont reliées à une source de tension alternative. Les mesures seront
donc effectuées en valeurs efficaces (la valeur du courant continu ou de la tension continue
produisant un échauffement identique dans une résistance). L’exploration spatiale du potentiel
dans l’électrolyte se fait à l’aide d’une sonde reliée à un voltmètre V. On relie une des électrodes
à la terre, de façon à ce qu’elle soit au potentiel zéro (E2sur la Fig. 8).
E1 E2
GBF
voltmètre
sonde
cuve +
eau
FIGURE 8 – Cuve rhéographique alimentée par un montage potentiomé-
trique
1. Faites le montage de la Figure 8. Alimentez-le avec une tension sinusoïdale d’amplitude
suffisante (quelques volts). Veillez à bien en choisir la fréquence. Justifiez.
2. Dans cette configuration, tracez la carte des équipotentielles sur du papier millimétré et
décrivez la manière dont vous avez procédé aux mesures.
3. Tracez le potentiel en fonction de x. Quelle est la forme de la fonction V(x) ? Déduidez-en
la valeur du champ électrique entre les deux électrodes. Dessinez les lignes de champ et
comparez à ce que vous avez tracé en préparation de TP.
Ajoutez un conducteur cylindrique au centre de la cuve (Fig. 9).
4. De la même manière, tracez les équipotentielles. En déduire la forme des lignes de champ
et comparez à ce que vous avez tracé en préparation de TP.
5. On veut vérifier qu’à la surface du cylindre l’expression du champ électrique est :
Esurface =
σ0
cosθ
n
11

E1 E2
GBF
voltmètre
ș
n
FIGURE 9 – Conducteur cylindrique dans la cuve rhéographique.
où σ0est une densité surfacique de charges et  nle vecteur unitaire normal à la surface
du cylindre. Pour cela, il faut mesurer le champ électrique à la surface du cylindre avec
E=−
−−−→
gradV.Pourunangleθdonné, que vous repérerez grâce au papier gradué en angle,
mesurez la différence de potentiel δVsur une courte distance δx. Répétez la mesure pour
différentes valeurs de θ. Vérifiez alors la dépendance du champ électrique avec l’angle θ.
2. – Images électriques - Dipôle
Le but de l’expérience est d’obtenir une cartographie des potentiels et des lignes de champ
d’un « dipôle » électrostatique et d’aborder la notion d’image électrique. Dans la cuve rhéogra-
phique, on va alors étudier les deux configurations (a) et (b) (cf. Fig.10). Attention : on prendra
soin de garder un gradient de potentiel constant lors du changement de configuration (δV/δx
identique pour config. a et b).
E1 E2
GBF
voltmètre
E1 E2
(a) (b)
FIGURE 10 – Images électriques dans la cuve rhéographique
1. Déterminez expérimentalement les équipotentielles dans les configurations a et b pro-
posées.
2. Tracez les lignes de champ et calculez, pour chaque configuration, la valeur du champ en
quelques points.
3. Vérifiez que les lignes de champ et les surfaces équipotentielles pour le « dipôle » de la
configuration (a) et pour la charge et le plan métallisé de la configuration (b) sont les
mêmes (image électrique).
12