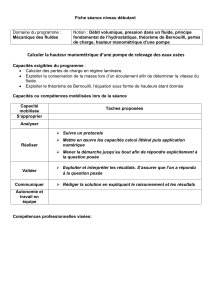
Un fluide circule dans un conduit dont la section augmente

LPAI, 2007-2008, applications du théorème d’Euler, propulsion, Daniel Huilier
Application du Théorème d’Euler : Effort sur un diffuseur
Un fluide circule dans un conduit dont la section augmente progressivement, passant de Ae à As
> Ae|. On pose a : Ae/As (0 < α < 1). Un tel écoulement soumet la conduite à un effort qu'il s'agit
de calculer en négligeant les forces de pesanteur et de viscosité. Les profils de vitesse et de
pression seront pris uniformes dans les deux sections, Ae et As.
L'application du théorème d'Euler donne :
dSnpnApnApnAVnAV
S
ssseeess
2
see
2
e
r
r
r
r
r∫∫
−−−=ρ+ρ
Domaine de contrôle pour I'application du théorème d'Euler à l'écoulement dans un diffuseur.
L'égalité précédente montre que la conduite exerce sur le fluide une force colinéaire au sens de
l'écoulement et de module
()()
e
2
ees
2
ss
S
AVPAVPdSnp ρ+−ρ+=− ∫∫ r
On retrouve la différence de dynalpie (pression statique + pression dynamique) entre la sortie et
l'entrée dans le diffuseur. En supposant que vitesses et pressions satisfont la relation de Bernoulli
entre les sections amont et aval du diffuseur, le résultat précédent peut encore s'exprimer à partir
des valeurs prises soit dans la section d'entrée, soit dans celle de sortie. On trouve alors :
Avec la relation de Bernouilli qui donne :
2
ss
2
ee V
2
1
PV
2
1
Pρ+=ρ+
et l’équation de conservation de la masse :
ssee AVAV
ρ
=
ρ
1

LPAI, 2007-2008, applications du théorème d’Euler, propulsion, Daniel Huilier
e
2
ee A.V
2
1
P
1
F⎥
⎦
⎤
⎢
⎣
⎡ρ
α−
+
α
α−
=
s
2
ss A.V
2
1
P
1
F⎥
⎦
⎤
⎢
⎣
⎡ρ
β−
+
β
β−
=
Où l’on a posé
e
s
A
A
1=
α
=β
Les expressions ci –dessus sont positives de sorte que la force qu'exerce le divergent sur le fluide
a même sens que l'écoulement, et par réaction, le fluide tend à faire "reculer" le divergent. On
pourra, par un raisonnement analogue, étendre ces conclusions au cas d'un convergent.
Hélice classique
Une hélice est un dispositif qui peut soit transmettre à un écoulement, soit recevoir de celui-ci
une certaine puissance mécanique. Dans le premier cas, elle est utilisée comme moyen de
propulsion, la mise en mouvement du fluide s'accompagnant, par réaction, d'une force de traction
sur les pales de l'hélice. Dans le second cas, elle sert à convertir une partie de l'énergie cinétique
du fluide en travail sur son arbre. Ces deux modes d'utilisation sont schématisés sur la figure 12
et correspondent à des applications de moteurs, pour la propulsion tant aérodynamique
qu'hydrodynamique d'une pale, et d'éolienne de l'autre.
En négligeant la compressibilité du fluide, les effets de viscosité et le mouvement de giration du
fluide, on peut considérer que le passage à travers une hélice motrice se traduit pour le fluide par
une accélération et pour une hélice réceptrice, par une décélération. Il en résulte des effets
respectifs qui, se produisant dans un milieu ambiant de pression constantes, sont à l’origine de
forces appliquées au fluide. C'est la résultante de ces forces qu'il s'agit de calculer.
Solution :
Désignant par F la résultante de la force exercée sur le fluide par l’hélice, l'application du
théorème d'Euler au domaine - voir figure 2 - limité par la surface 'SASA se ++
+
=
Σ
donne :
∫∫∫∫∫∫ Σ
−+=ρ+ρ dSnPFdSnVdSnV a
A
s
2
s
A
e
2
e
se
r
r
r
r
2

LPAI, 2007-2008, applications du théorème d’Euler, propulsion, Daniel Huilier
soit finalement, avec des profils de vitesses uniformes
(
)
ss
2
se
2
en.AVAVF
r
r
ρ+ρ−=
Par ailleurs, la conservation du débit massique impose : mssee QAVAV
=
ρ
=
ρ
de sorte que la résultante s'écrit finalement :
sesm n)VV.(QF
r
r
−=
Pour une hélice motrice, Vs -Ve est positif et la force produite par le fluide sur l'hélice (- F
r
)
s'exerce clans le sens opposé à l'écoulement, le résultat s'inversant pour une hélice fonctionnant
en récepteur.
Poussée d'une turbomachine
Le fonctionnement d'un turboréacteur peut être décrit de façon très schématique de la façon
suivante : Un débit massique de fluide Qm est admis en entrée de la machine. Il y est ensuite
comprimé puis reçoit un débit qf de carburant. Le mélange est alors brûlé dans une chambre de
combustion ce qui a pour effet d'en augmenter la température et donc l'énergie (enthalpie totale
en fait). Une part de cette énergie sert à actionner une turbine qui entraine le compresseur, l'autre
part est émise, après détente dans une tuyère, sous forme cinétique et thermique dans le jet de
sortie de la machine. C'est la quantité de mouvement ainsi libérée qui est à l'origine, par réaction
de la poussée de l'engin qu'il s'agit de calculer.
Solution
Considérons alors un domaine de contrôle Δ tel que celui représenté à la figure 3. En négligeant
le débit de carburant (qf << Qm), tout se passe, du point de vue du bilan de quantité de
mouvement sur A, comme si le débit massique Qm de fluide subissait une accélération axiale,
passant d 'une vitesse d 'admission Va à une vitesse d'éjection Ve >> Va.
Fig.3: Domaine de contrôle pour l'application du théorème d'Euler à une turbomachine.
Le théorème d'Euler appliqué au domaine limité par la surface 0ae SASA +
+
+
=
Σ
donne :
dSnpdSnpnApnApnAVnAV
S0S
eeeaaaee
2
eeaa
2
aa
r
r
r
r
r
r∫∫∫∫ −−−−=ρ+ρ
3

LPAI, 2007-2008, applications du théorème d’Euler, propulsion, Daniel Huilier
en prenant les profils de vitesse et pression uniformes à l'admission (section Aa) et à l'éjection
(section Ae). La résultante des forces exercées par le fluide interne sur la machine vaut donc :
∫∫∫∫ +ρ++ρ++=−=
0S
ee
2
eeeaa
2
aaa
S
int dSnPnA)VP(nA)VP(dSnPF r
r
r
r
r
Nous admettrons qu'en première approximation la pression statique est la même sur toutes les
frontières libres du domaine Δ et égale à . La relation précédente devient :
∞
P
∫∫
∞∞∞ +ρ++ρ++=
0S
ee
2
eeaa
2
aaint dSnPnA)VP(nA)VP(F
r
r
r
r
Par ailleurs, le fluide extérieur exerce sur la face externe de la surface S une résultante de
pression qui vaut :
∫∫ ∞
−=
S
extext dSnPF
r
r
De sorte que la résultante des forces appliquées à la machine par le fluide tant interne qu’externe
vaut :
∫∫∫∫ ∞∞∞∞ −−ρ+−ρ+−=+−=
S0S
ee
2
eeaa
2
aaextint dSnPdSnPnA)VP(nA)VP(FFR r
r
r
r
rrr
Il apparaît ainsi que l’ensemble des contributions mettant en jeu la pression P∞ est nul puisque
regroupé sur la surface fermée Σ. On en déduit que la poussée du moteur vaut finalement :
aaeae
2
eea
2
aa n)VV(Qmn)AVAV(R
r
r
r
−=ρ+ρ−=
En vol stationnaire, la poussée/réaction, de signe opposée à Va est exactement compensée par la
force de traînée, T, s’exerçant sur la surface d’un avion par exemple. La puissance dissipée par la
traînée , ou puissance employée à cette propulsion, vaut :
)VV(QmVV.R aeaa
−
=
Le gain en énergie cinétique ( en termes de puissance), soit la puissance fournie à l’air pour
accroître son énergie cinétique, vaut :
)VV)(VV(VA
2
1
VQ
2
1
V.Q
2
1
Paeaeee
2
am
2
em +−ρ=−=
Le rendement est donné par :
ea
aa
VV
V2
P
RV
+
==η
Ve est nécessairement supérieure à Va, η est toujours inférieur à 1, mais il tend vers 1 si Va tend
vers Ve.
4