FSA - UIZ - UNIVERSITE IBN ZOHR

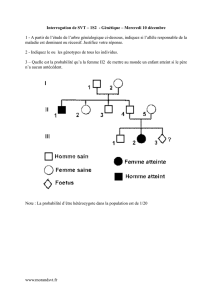
Génétique des populations SV5 chapitre 5 Page 38
CHAPITRE 5 : SELECTION MODELE DE BASE
prmi les forces susceptibles de modifier la constitution génétique des populations,
figure la sélection. Darwin a fait de la sélection naturelle le moteur de l'évolution ; une
partie de l'amélioration agronomique repose sur la sélection et le rôle de celle-ci a été
formalisé dès les premiers modèles de la génétique des populations.
Il y a sélection si les différents génotypes ne participent pas de façon égale à la
constitution génotypique de la génération suivante. Ainsi, un génotype donné à un
avantage sélectif sur un autre lorsque les individus de ce génotype laissent un plus grand
nombre de descendants fertiles à la génération suivante.
1) Fitness, valeur adaptative et coefficient de sélection
Lorsque les individus de génotypes différents montrent une viabilité ou une
fécondité différente, chaque génotype est caractérisé par sa performance, c'est-à-
dire sa capacité à participer à la génération suivante. Cette mesure est appelée valeur
sélective, fitness, ou valeur adaptative. Par définition, la fitness ou valeur sélective d ’un
génotype correspond au nombre de descendants viables et fertiles que produit en
moyenne chaque individu de ce génotype à la génération suivante.
La valeur sélective ou fitness d'un génotype dépend principalement de sa survie entre le
stade zygote (oeuf) et le stade adulte, et de sa fertilité (nombre de descendants viables
capables de se reproduire). Ces deux paramètres déterminent le nombre de descendants
produits en moyenne par cette catégorie génotypique. Une définition simple de la fitness
peut donc être donnée par la formule :
Fitness = Survie x Fécondité
a)Fitness absolue
On appelle fitness absolue, notée W, la valeur issue de la mesure de la probabilité
de survie et de la fertilité de chaque catégorie génotypique et qui détermine
directement leur nombre moyen de descendants. Pour un gène à deux allèles A et a,
les valeurs de fitness seront notées de la façon suivante :
Génotype
AA
Aa
aa
Fitness absolue
WAA
WAa
Waa

Génétique des populations SV5 chapitre 5 Page 39
L'exemple ci-dessous illustre comment la fitness absolue de ces génotypes peut être
estimée:
b) Fitness relative et coefficient de sélection
La performance des génotypes est cependant toujours définie de façon relative =
fitness relative notée  de façon à ce que la plus forte valeur de fitness soit égale
à 1. La fitness relative d'une catégorie d'individus est le rapport entre sa fitness
absolue W et la plus forte valeur de fitness absolue (Wmax) observée dans la
population.
Fitness relative  = W / Wmax
avec 0 <  < 1
Dans le cas d'un gène à 2 allèles A et a :
AA=WAA/Wmax
Aa=WAa/ Wmax
aa = Waa/ Wmax
La différence entre  et 1 est appelée coefficient de sélection, noté s, qui est une
mesure du taux de réduction de la fitness de chaque catégorie génotypique par
rapport à la meilleure dans cette population.
AA = 1 - sAA
Aa = 1- sAa
aa =1-saa
Ainsi, dans l'exemple précédent, les fitness relatives des génotypes sont les suivantes
:
Génotypes
AA
Aa
aa
Fitness absolue
wAA= 1,125
wAa= 1
waa=0,5
Fitness relative
AA=1,125 /1,125
AA=1
Aa=1 /1,125
Aa=0,89
aa=0,5 /1,125
aa =0,44
Coeff. de sélection
sAA=0
sAa=0,11
saa=0,56

Génétique des populations SV5 chapitre 5 Page 40
A. LE MODELE DE BASE DE LA SELECTION
Nous allons considérer une population panmictique, d'effectif suffisamment grand
pour que les fréquences alléliques ne soient pas affectées par d'autres facteurs que la
sélection. On suppose également que l'action des facteurs sélectifs reste la même au
cours des générations et que celles-ci ne se chevauchent pas. Dans cette population, soit
un gène A existant sous 2 formes alléliques A1 et A2 dont les fréquences respectives à
la génération n sont p et q
1. SELECTION SUR LA PHASE DIPLOÏDE
Dans ce modèle, les individus diploïdes qui sont soumis à l'action de la sélection
et les différents génotypes ont une capacité d'adaptation différente. Nous
raisonnerons toujours sur le couple d'allèles (A1 : p ; A2 : q). Nous avons donc trois
génotypes possibles auxquels nous affecterons respectivement les valeurs sélectives
suivantes :
A1A1 : σ1 A1A2 : σ 2 A2A2 : σ 3
Dans le modèle le plus simple que nous allons examiner, ces valeurs représentent
l'ensemble des composantes de la valeur sélective de chaque génotype pour la période
pré-reproductrice (survie embryonnaire, survie larvaire, ou juvénile ...). Elles
correspondent au nombre moyen de descendants laissés à la génération suivante par
chacun des génotypes. Seule la situation dans laquelle la sélection opère entre la
fécondation et l'âge de la reproduction est envisagée ici.
1.1 Relation entre 2 générations successives
L'évolution de la population, étudiée par la variation des fréquences génotypiques,
dépend donc des rapports existant entre les valeurs sélectives.
Génotypes à la génération n A1A1 A1A2 A2A2
En panmixie, les fréq. parmi
les zygotes formés sont : p2 2 pq q2
Valeurs sélectives : σ1 σ2 σ3
Après action de la sélection
cette composition est modifiée : σ1p2 2 σ2pq σ3q2

Génétique des populations SV5 chapitre 5 Page 41
Soit : = σ1 p2 + 2 σ2 pq + σ 3q2
Cette somme n'est plus égale à 1, la fréquence des trois génotypes après la
sélection est donc :
Fréq. des génotypes à la
génération n+1 : σ1p2/ 2 σ2pq / σ3q2/
La fréquence de l'allèle A1 est devenue :
p'= σ1p2/ + (2 σ2pq / ) = [p(pσ1+q σ2)]/
représente la valeur sélective moyenne de la population. Elle est la moyenne
pondérée des valeurs sélectives des différents génotypes et correspond au nombre
moyen des descendants par individu de la nème génération.
On calcule alors l'accroissement p
p = p' - p = [p(pσ1+q σ2)]/ - p
Après réduction au même dénominateur et mise en facteur nous obtenons :
p étant la fréquence de l'allèle A1 à la nième génération.
Cette formule classique se condense en une expression plus généralisable. On
remarque que la dérivée de W par rapport à p s'écrit :
dW/dp = d[p² σ1+2p(1-p) σ2+(1-p)² σ3]/dp
= 2 σ1p + 2 σ2 (1 – 2p) - 2 σ3 (1-p)
= 2 [(σ 1 - σ 2) p + (σ 2 - σ 3) q ]
c'est- à- dire le double du numérateur du p trouvé précédemment. Le p peut alors
s'écrire :
W
W
W
W
W
1
2
W
W
W
W

Génétique des populations SV5 chapitre 5 Page 42
1.2 Généralisation de la formule
L'expression  se généralise dans le cas d'individus polyploïdes ou pour des
gènes liés au sexe. Wright (1945) démontre que lorsque les valeurs sélectives sont
peu différentes la formule est :
Avec k = 1 chez les haploïdes ; k = 2 chez les diploïdes et k = 4 chez les
autotétraploïdes (luzerne par exemple).
1.3 Utilisation des formules
Etude du p
Pour analyser l'évolution de populations soumises à une sélection agissant sur la
phase diploïde, on étudiera la variation de p . On examine ainsi les variations de
fréquences de l'allèle A1 au cours des générations.
y = /2 = (σ 1 - 2 σ 2 + σ 3) p + σ 2 - σ 3
Analyse de y en fonction des σ i
Le domaine de définition de y est [ -  , +  ], mais seul nous intéresse l'intervalle [ 0 ; 1
]. Le graphe de cette fonction est une droite de pente (σ 1 - 2 σ 2 + σ 3) et d'ordonnée à
l'origine (σ 2 - σ 3). Quatre cas sont à examiner selon que y est toujours de même signe
entre 0 et 1, ou qu'il change de signe entre ces deux valeurs. L'étude de ces différents
cas est simple, le graphe étant une droite, il suffit de choisir 2 points particuliers. Nous
prendrons les points d'abscisse 0 et 1, les valeurs correspondantes de y sont :
p = 0 y = σ 2 - σ 3
p = 1 y = σ 1 - σ 2
Cas n° 1 (voir figure1). σ 1 > σ 2 > σ 3
fig.1
W'