Travaux Dirigés de O1

TD – O1Énoncé PCSI22016 – 2017
Travaux Dirigés de O1
Conseils pour ce TD :
•Toujours commencer par effectuer un (beau) tracé aussi précis que possible (règle, couleurs ...).
Tracer les rayons lumineux en traits pleins et les orienter. Tracer leur prolongement en pointillés.
Orienter les angles et respecter les lois de Snell Descartes (par exemple, le rayon réfracté se rapproche
de la normale au dioptre quand on passe dans un milieu plus réfringent).
•Dans l’expression des lois de Snell Descartes, les angles sont orientés de la normale au rayon et non
du miroir ou du dioptre au rayon.
•En général, pour résoudre l’exercice, on utilisera les lois de Snell Descartes et des relations mathé-
matiques connues : somme des angles orientés dans un triangle, relations trigonométriques dans un
triangle rectangle.
On a ensuite à combiner ces différentes relations, c’est pourquoi on aura souvent à travailler dans des
triangles rectangles ayant un coté commun. De même, on privilégiera les relation trigonométriques
faisant apparaître un sinus car il apparaît également dans la loi de la réfraction.
•Vérifier la cohérence entre les résultats issus du calcul et la figure.
Exercice 1 : Loi de Cauchy
La formule de Cauchy simplifiée, donnant l’indice d’un verre pour une radiation monochromatique
de longueur d’onde λest : n=A+B
λ2où Aet Bsont des constantes.
1. Quelles sont les dimensions et unités légales de Aet B.
2. Des mesures effectuées avec un même verre ont donné :
•nr= 1,618 pour une radiation rouge de longueur d’onde dans le vide λr= 768 nm et
•nv= 1,652 pour une radiation violette de longueur d’onde dans le vide λr= 434 nm.
(a) Calculer les valeurs de Aet B.
(b) Déterminer la valeur de l’indice njpour une radiation jaune de longueur d’onde dans le
vide λj= 589 nm.
Exercice 2 : Loi de la réfraction
Un rayon lumineux dans l’air tombe sur la surface d’un liquide ; il fait un angle α= 56◦avec le plan
horizontal. La déviation entre le rayon incident et le rayon réfracté est θ= 13,5◦. Quel est l’indide n
du milieu.
Exercice 3 : Aquarium
e
i1
i2
i3
air verre eau
La paroi d’un aquarium est constituée d’une lame de verre à
faces parallèles, d’épaisseur e= 5 mm.
L’indice optique de l’air est n1= 1,00 ,celui du verre est n2=
1,50 et celui de l’eau n3= 1,33.
1. Sachant que i1= 46˚, calculer i2et i3.
2. Voit-on toujours tout le contenu de l’aquarium ?
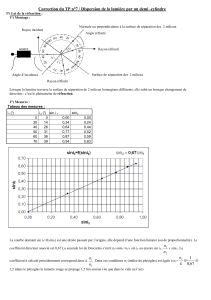
Exercice 4 : Mise en évidence de faibles rotations
Un pinceau lumineux arrive perpendiculairement en Ià la surface d’un miroir plan (M). Ce miroir
peut tourner autour d’un axe ∆ passant par Iet perpendiculaire au plan d’incidence.
1

PCSI22016 – 2017 Énoncé Lois de l’optique
1. Le miroir tourne d’un angle αautour de ∆. De quel angle βtourne le rayon réfléchi dans le
même temps ?
2. À la distance D= 1 m, on place une règle Rgraduée perpendiculaire au pinceau réfléchi. Le
plus petit déplacement visible de la tache lumineuse réfléchie arrivant sur la règle est dmin = 1
mm. Quel est le plus petit angle de rotation mesurable avec ce dispositif ?
Exercice 5 : Construction d’Huygens
Cette construction géométrique permet de construire le rayon réfracté correspondant à un rayon
incident donné.
I
i1
n1
n2
Du point d’incidence Icomme centre, on trace deux demi-cercles de rayons 1
n1et 1 n2.
On prolonge le rayon incident jusqu’à ce qu’il rencontre le demi-cercle de rayon 1
n1.
Du point d’intersection T, on mène la tangente qui coupe le dioptre en H.
À partir de H, on mène la tangente à l’autre demi-cercle ce qui définit un point T′.
Le rayon réfracté est alors IT ′.
1. Suivre le mode opératoire dans les deux cas : n1< n2et n1> n2.
2. Vérifier que cette construction est bien conforme aux lois de Snell-Descartes.
3. Retrouver les cas de la réfraction limite et de la réflexion totale.
Exercice 6 : Lame à faces parallèles
e
i
vide
n
vide
d
1. Construire le rayon transmis par une lame à faces paral-
lèles en verre d’indice de réfraction net d’épaisseur e. Ce
rayon existe-t-il toujours ?
2. Quelle est la direction du rayon réfracté si le rayon inci-
dent arrive sous l’incidence i?
3. Déterminer la distance dqui sépare la direction du rayon
incident de celle du rayon transmis (Cf. figure)
Application numérique : n= 1,5, e= 1 cm et i= 45˚.
Exercice 7 : Éclairage d’un bassin
Un bassin de profondeur h= 1 m est totalement rempli d’eau, d’indice n≃1,33.
L’indice de l’air sera pris égal à 1.
Au fond du bassin est placé une source ponctuelle émettant de la lumière dans toutes les directions.
Quel est le rayon rdu disque lumineux qui se forme à la surface de l’eau ?
Exercice 8 : Mesure de l’indice d’un liquide.
Une cuve en verre à la forme d’un prisme de section droite rectangle isocèle. Elle est posée horizonta-
lement sur une des arêtes de longueur ldu triangle isocèle, et le sommet opposé à ce coté est ouvert
pour permettre de remplir la cuve d’un liquide transparent d’indice n. Un pinceau de lumière est
envoyé horizontalement sur la face verticale de la cuve, dans le plan de section droite et à la hauteur
l/2.
Ce rayon émerge au delà de l’hypoténuse et rencontre en un point Pun écran Eplacé verticalement à
la distance lde la face d’entre du dispositif. On néglige l’effet dû aux parois en verre sur la propagation
du pinceau de lumière.
En P, on observe sur l’écran une tache du pinceau à la hauteur z, repérée par rapport à l’horizontal
formée par le bas de la cuve.
1. Faire un dessin du dispositif.
2. Quelle valeur supérieure peut-on donner à la valeur de l’indice n?
2

TD – O1Énoncé PCSI22016 – 2017
3. Exprimer nen fonction de let z. On prendra l
2−zfaible.
Faire l’application numérique pour l= 30 cm et z= 14,7 cm.
Exercice 9 : Méthode de mesure de l’indice d’un liquide.
Verre (n)
Liquide (n1)
α
On éclaire la face gauche du cube de verre sous différentes
incidences.
La goutte de liquide apparaît brillante à partir de α= 75˚56′
(75 degrés et 56 minutes).
L’indice du verre est n= 1,5200, celui de l’air est nair =
1,0000.
En déduire la valeur de l’indice du liquide n1< n.
Exercice 10 : Rayon de courbure
Une fibre optique est constituée d’une âme en verre d’incide n1= 1,66 et de diamètre d= 0,05 mm
entourée d’une gaine en verre d’indice n2= 1,52. On courbe la fibre éclairée sous incidence normale.
L’axe de symétrie de la fibre décrit un cercle de rayon Rappelé rayon de courbure.
1. Faire un schéma de la situation et tracer la propagation de plusieurs rayon incident au travers
de la fibre.
2. Quel est le de courbure Rminimal pour lequel toute la lumière incidente traverse la fibre ?
Exercice 11 : Étude d’un Prisme
n
S
A
I
D
I′
D
irr′
i′
On appelle prisme un milieu transparent que
nous supposerons homogène et isotrope d’in-
dice nlimité par deux dioptres plans non pa-
rallèles. On appelle arête du prisme la droite
selon laquelle se coupent les deux dioptres et
plan de section principale tout plan perpendi-
culaire à l’arête. La figure ci-contre est faite
dans un plan de section principale. Nous sup-
poserons que le prisme baigne dans l’air d’in-
dice nair ≃1.
1. Montrer que l’étude est limité à un plan de section principale c’est à dire que les trois rayons
sont contenu dans le plan de la figure.
2. On cherche à établir les relations du prisme :
(a) Écrire les lois de Snell-Descartes en Iet I′: relations (1) et (2)
(b) Déterminer une relation entre A,ret r′: relation (3)
(c) La déviation du prisme Dest l’angle que fait le rayon émergent (s’il existe) avec le rayon
incident. Calculer De, fonction de iet i′: relation (4). En déduire une relation entre D,
Aet nsi iet Asont faibles.
3. À quelle condition sur Ay a-t-il un rayon émergent ?
4. Étude de la déviation D
(a) Pour une radiation monochromatique λdonnée, établir l’expression de dD
di en fonction de
i,r,i′et r′et en déduire que la déviation passe par une valeur minimale Dmlorsque i
varie.
(b) Montrer alors que, dans le prisme, la lumière se propage orthogonalement au plan bissec-
teur.
(c) Établir l’expression de nen fonction de Aet Dm.
3