COULEUR DES CORPS CHAUFFÉS

AE4 - Observer
COULEUR DES CORPS CHAUFFÉS
Objectifs :
 Connaître les limites en longueur d’onde dans le vide du domaine visible et situer les rayonnements infrarouges et
ultraviolets
 Exploiter la loi de Wien
Capacités travaillées
4
– Extraire des informations sur des supports variés
8
– Proposer une hypothèse
10
– Exploiter des observations, des résultats, des mesures
16
– Tracer un graphique
En classe de 2
nde
, il a été vu qu’un corps chaud émet un rayonnement dont le spectre est continu et dépend
de la température. De plus, le spectre de ce rayonnement s'enrichit en petites longueurs d'ondes du domaine
visible (bleu et violet) lorsque sa température augmente.
1. La tête dans les étoiles
Bételgeuse et Bellatrix sont deux étoiles appartenant à la constellation d’Orion, qui est très facilement visible
dans le ciel des nuits d’hiver.
Bételgeuse est une étoile rouge et Bellatrix une étoile bleue.
 Proposer une hypothèse permettant d’expliquer la couleur de ces étoiles
2. Intensité lumineuse et longueur d’onde
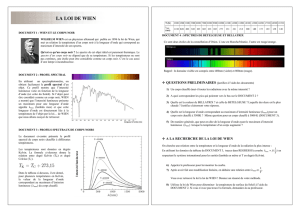
Ci-après, voici le graphe représentant l’intensité lumineuse émise (unité arbitraire) en fonction de la longueur
d’onde (nm) pour des corps de températures différentes.
Remarque : La température d’un corps peut s’exprimer en Kelvin (K). Elle est reliée à la température θ en degré
Celsius (°C) par la relation : T = θ + 273,15.
a. Tracer sur le graphe le domaine correspondant
aux radiations (en nm) visibles.
b. Indiquer si un corps chaud émet toutes les
radiations avec la même intensité. Justifier.
c. Pour un corps à 3500 K, indiquer la longueur
d’onde λ
max
correspondant au maximum
d’intensité lumineuse. Faire de même pour un
corps à 5000 K.
d. Conclure en indiquant l’évolution de la
longueur d’onde (λ
max
) ayant le maximum
d’intensité lumineuse en fonction de la
température (T).
Spectre du Domaine Visible
3. La loi de Wien
Dans le tableau ci-dessous, il est donné, pour plusieurs températures en Kelvin, la valeur de la longueur d’onde
correspondant au maximum d’émission lumineuse d’un corps chauffé.
Le modèle :
T (K) 2000 2500 3500 4500 5500 6500 7500 8500 9500 10500
λ
max
(nm) 1450 1156 826 642 526 445 385 345 305 275
T (K) 11500 12500 13500 14500 15500 16500 17500 18500 19500
λ
max
(nm) 251 231 214 200 186 175 165 156 148
a. En vous aidant de la réponse à la question d de la partie 2, indiquer quel graphe tracer afin de vérifier la
loi de Wien.
b. A l’aide d’un logiciel graphique tracer ce graphique
c. Modéliser ensuite le graphe obtenu par une droite (comme lors de l’AE1 sur les lentilles), obtenez
l’équation de cette droite et en déduire l’expression de la loi de Wien.
4. De retour dans les étoiles…
La température de surface de Bételgeuse est de 3500 K et celle de Bellatrix est de 28 000 K.
Couleur
Rouge Orangé Jaune Vert Bleu Indigo Violet
λ (nm)
800 à 650 650 à 590 590 à 550 550 à 490 490 à 465 465 à 440 440 à 400
La loi de Wien relie la température T d’un corps chaud et la longueur d’onde du maximum
d’intensité lumineuse max. La température T s’exprime en kelvin (K) et la longueur d’onde
max en nanomètre (nm).
La constellation d’Orion
a.
Calculer la longueur d’onde du
maximum d’intensité lumineuse pour
Bételgeuse et Bellatrix.
b. Conclure sur la couleur de ces étoiles.
c. Indiquer si votre hypothèse de la partie 1
est validée ou non.