étude simplifiée d`une dérive génétique : modélisation et

ÉTUDE SIMPLIFIÉE D'UNE DÉRIVE GÉNÉTIQUE :
MODÉLISATION ET MISE EN ŒUVRE AVEC R
(A PARTIR D'UN CAS PROPOSÉ EN PLURI PAR FABRICE LECLERCQ)
CAS CONCRET ET PREMIÈRE MODÉLISATION (MODÈLE A)
L'exemple est tiré du livre "Guide critique de l'évolution", sous la direction de Guillaume Lecointre,
(éditions Belin). Un travail avec les enseignants de biologie doit permettre de préciser la problématique
biologique.
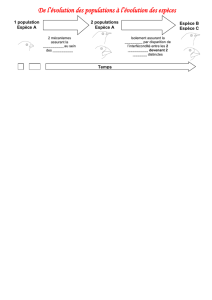
Il s'agit d'étudier l'évolution des espèces d'une population d'escargots, tout au long de plusieurs générations.
On modélise une évolution particulière en partant des hypothèses suivantes :
H1 : La population est isolée (sur un îlot), il n'y a donc pas d'apport extérieur.
H2 : La population de départ est constituée de 6 individus de 6 espèces différentes que l'on appellera au
départ "Blanc", "Bleu", "Rouge", "Jaune", "Vert", "Noir" puis, pour des raisons pratiques de
programmation, "violet", "blue", "red", "yellow", "green", "black".
H3 : À chaque génération, chaque espèce donne naissance à un nombre de petits de 1 à 6, aléatoirement
distribué selon une loi uniforme discrète. L'ensemble de tous ces petits constitue la population initiale
(de départ) de chaque génération.
H4 : À chaque génération, ne survivent que 6 individus choisis au hasard dans la population initiale de la
génération en cours.
H5 : Ces 6 individus se reproduisent selon l'hypothèse H3, les génération se succèdent donc de la même
façon.
L'étude portera sur les 4 aspects suivants :
aspect 1 : Le nombre et le pourcentage de chaque espèce au début de chaque génération, avec une
présentation dynamique.
aspect 2 : L'évolution, au cours des générations, du nombre d'individus de l'espèce qui reste seule au bout
d'un certain nombre de générations.
aspect 3 : La distribution du nombre de générations au bout duquel une espèce se retrouve seule sur l'îlot.
aspect 4 : La distribution des espèces se retrouvant seules au bout d'un certain nombre de générations.
L'utilisation de RStudio (ou Tinn-R en réorganisant les fenêtres de façon appropriée) permet de répéter
directement la même simulation (touches ↑ puis entrée) et d'observer l'effet graphique des variations des
distributions ou des fonctions obtenus à partir des séries simulées (cf. les copies d'écran en dernières pages).
PREMIÈRE MISE EN ŒUVRE DU MODÈLE A, EN LIGNES DE COMMANDES
POUR COMPRENDRE LES FONCTION R UTILISÉES
► Il s'agit d'observer l'évolution de la distribution des effectifs des espèces en début de chaque génération.
# DÉRIVE GÉNÉTIQUE CHEZ LES ESCARGOTS
# LES COMMANDES DE FABRICE LECLERCQ
# Simuler le jet d'un dé (dai)
(dai <- 1:6)
[1] 1 2 3 4 5 6
sample(dai, 1)
[1] 2
sample(dai, 6)
[1] 1 4 3 6 5 2
sample(dai, 6, replace = TRUE)
[1] 6 2 5 5 5 3
Hubert RAYMONDAUD 07/12/12
LEGTA LOUIS GIRAUD *
84200 CARPENTRAS page 1 sur 11 DeriveEscargots.odt

# Création de l'îlot initial (population parent)
ilot <- c("Blanc", "Bleu", "Rouge", "Jaune", "Vert", "Noir")
table(ilot)
ilot
Blanc Bleu Jaune Noir Rouge Vert
1 1 1 1 1 1
pie(table(ilot))
# La reproduction à la génération 1
(population <- rep(ilot, sample(dai, 6, replace = TRUE)))
[1] "Blanc" "Blanc" "Blanc" "Blanc" "Blanc" "Blanc" "Bleu" "Bleu" "Rouge"
[10] "Rouge" "Rouge" "Rouge" "Jaune" "Jaune" "Jaune" "Jaune" "Jaune" "Vert"
[19] "Noir" "Noir" "Noir" "Noir" "Noir" "Noir"
# Tableau des effectifs de la distribution des espèces au début de la génération 1 :
(tabloEspeces <- table(population))
population
Blanc Bleu Jaune Noir Rouge Vert
6 2 5 6 4 1
# Tableau des fréquences de la distribution des espèces au
# début de la génération 1 :
(tablEspeces <- tabloEspeces / sum(tabloEspeces))
population
Blanc Bleu Jaune Noir Rouge Vert
0.250 0.083 0.208 0.250 0.167 0.042
pie(tablEspeces, labels = paste(names(tablEspeces), "\n",
round(tablEspeces, 2)))
# Sur l'îlot la sélection naturelle fait que seuls 6 escargots choisis au
# hasard vont survivre et se reproduire. On aura alors la génération 2
ilot <- sample(population, 6)
[1] "Noir" "Jaune" "Noir" "Blanc" "Rouge" "Blanc"
# Et le cycle recommence, pour aboutir à la génération 2 :
(population <- rep(ilot, sample(dai, 6, replace = TRUE)))
[1] "Noir" "Noir" "Noir" "Noir" "Jaune" "Jaune" "Jaune" "Noir" "Noir"
[10] "Noir" "Blanc" "Blanc" "Blanc" "Blanc" "Blanc" "Blanc" "Rouge" "Rouge"
[19] "Rouge" "Rouge" "Blanc" "Blanc" "Blanc" "Blanc" "Blanc" "Blanc"
(tabloEspeces <- table(population))
population
Blanc Jaune Noir Rouge
12 3 7 4
(tablEspeces <- tabloEspeces / sum(tabloEspeces))
population
Blanc Jaune Noir Rouge
0.4615385 0.1153846 0.2692308 0.1538462
pie(tablEspeces, labels = paste(names(tablEspeces), "\n",
round(tablEspeces, 2)))
Hubert RAYMONDAUD 07/12/12
LEGTA LOUIS GIRAUD *
84200 CARPENTRAS page 2 sur 11 DeriveEscargots.odt

DEUXIÈME MISE EN ŒUVRE DU MODÈLE A AVEC UNE FONCTION R PLUS
PRATIQUE À UTILISER
► On fait afficher la successions des tableaux des effectifs des espèces des populations en début de chaque
génération. On fait afficher la succession des graphiques en secteurs des fréquences correspondantes. Une
phrase annonce l'espèce restant seule en fin de dérive, au bout de "gen" générations.
# F. LECLERCQ PROGRAMME 1
DerivEscar1 <- function(){
dai <- 1:6 ; gen <- 1
ilot <- c("white", "blue", "red", "yellow", "green", "black")
while(length(unique(ilot)) > 1){
population <- rep(ilot, sample(dai, 6, replace = TRUE))
ilot <- sample(population, 6)
tablEffEspeces <- table(population)
cat("Génération numéro", gen, "\n")
print(tablEffEspeces)
tablFreqEspeces <- tablEffEspeces / sum(tablEffEspeces)
pie(tablFreqEspeces, labels = paste(names(tablFreqEspeces), "\n",
round(tablFreqEspeces, 2)), col = names(tablEffEspeces),
main = paste("Distribution des espèces dans la \n",
"population initiale de la génération", gen))
Sys.sleep(3)
gen <- gen + 1
}
cat("\nLa dérive génétique a abouti à l'unique espèce :\n",
unique(ilot), "à la génération", gen, "\n\n")
}
> DerivEscar1()
Génération numéro 1
population
black blue green red white yellow
2 2 2 5 3 1
Génération numéro 2
population
black blue red white
3 10 1 4
Génération numéro 3
population
blue white
5 10
Génération numéro 4
population
blue white
3 18
La dérive génétique a abouti à l'unique espèce :
white à la génération 5
Avec les icônes de la fenêtre plot, il est
possible de revoir les graphiques en secteur de toutes
les générations représentées dynamiquement.
Hubert RAYMONDAUD 07/12/12
LEGTA LOUIS GIRAUD *
84200 CARPENTRAS page 3 sur 11 DeriveEscargots.odt

TROISIÈME MISE EN ŒUVRE DU MODÈLE A AVEC UNE FONCTION R
► La fonction R réalise un tableau récapitulatif des effectifs de toutes les espèces présentes en début de
génération. Elle fait un graphique en ligne brisée de l'évolution de l'effectif de l'espèce qui reste seule sur
l'îlot.
DerivEscar2 <- function(){
dai <- 1:6 ; gen <- 2
ilot <- c("violet", "blue", "red", "yellow", "green", "black")
PopIlots <- table(rep(ilot, sample(dai, 6, replace = TRUE)))
names(PopIlots) <- c("black", "blue", "green", "red", "violet", "yellow")
while(length(unique(ilot)) > 1){
population <- rep(ilot, sample(dai, 6, replace = TRUE))
ilot <- sample(population, 6)
tablEffEspeces <- table(population)
tab0 <- rep(0, 6)
names(tab0) <- c("black", "blue", "green", "red", "violet", "yellow")
tab0[names(tablEffEspeces)] <- tablEffEspeces
PopIlots <- rbind(PopIlots, tab0)
gen <- gen + 1
}
tab0 <- rep(0, 6)
names(tab0) <- c("black", "blue","green", "red", "violet", "yellow")
tablEffEspeces <- table(ilot)
tab0[names(tablEffEspeces)] <- tablEffEspeces
PopIlots <- rbind(PopIlots, tab0)
rownames(PopIlots) <- paste(rep("generation", gen), 1:gen, sep = "")
# Affichages des graphiques et résultats
cat("\nLa dérive génétique a abouti à l'unique espèce :\n",
unique(ilot), "à la génération", gen, "\n\n")
print(PopIlots)
plot(1:gen, PopIlots[ , unique(ilot)], type = "l", col = unique(ilot),
xlab = "Rang de la génération", ylab = "Effectif de l'espèce restante",
main = paste("Évolution de l'effectif de l'espèce", unique(ilot), "\npendant",
gen, "générations en début de génération"))
}
> DerivEscar2()
La dérive génétique a abouti à l'unique espèce :
red à la génération 12
black blue green red violet yellow
generation1 4 6 3 1 4 6
generation2 6 4 1 6 6 5
generation3 4 0 0 7 8 6
generation4 0 0 0 19 6 1
generation5 0 0 0 20 8 0
generation6 0 0 0 8 7 0
generation7 0 0 0 12 6 0
generation8 0 0 0 13 9 0
generation9 0 0 0 17 5 0
generation10 0 0 0 16 7 0
generation11 0 0 0 18 1 0
generation12 0 0 0 6 0 0
Hubert RAYMONDAUD 07/12/12
LEGTA LOUIS GIRAUD *
84200 CARPENTRAS page 4 sur 11 DeriveEscargots.odt

► Par rapport à DerivEscar2() La fonction R suivante DerivEscar2_1() réalise un graphique
supplémentaire en boites à pattes (boxplot) qui est une façon de résumer graphiquement les distributions
du nombre d'individus en début de génération, par espèce. C'est aussi une bonne illustration de la
"polyvalence" de la fonction grahique plot(...).
DerivEscar2_1 <- function(){
dai <- 1:6 ; gen <- 2
ilot <- c("violet", "blue", "red", "yellow", "green", "black")
PopIlots <- table(rep(ilot, sample(dai, 6, replace = TRUE)))
names(PopIlots) <- c("black", "blue", "green", "red", "violet", "yellow")
while(length(unique(ilot)) > 1){
population <- rep(ilot, sample(dai, 6, replace = TRUE))
ilot <- sample(population, 6)
tablEffEspeces <- table(population)
tab0 <- rep(0, 6)
names(tab0) <- c("black", "blue", "green", "red", "violet", "yellow")
tab0[names(tablEffEspeces)] <- tablEffEspeces
PopIlots <- rbind(PopIlots, tab0)
gen <- gen + 1
}
tab0 <- rep(0, 6)
names(tab0) <- c("black", "blue","green", "red", "violet", "yellow")
tablEffEspeces <- table(ilot)
tab0[names(tablEffEspeces)] <- tablEffEspeces
PopIlots <- rbind(PopIlots, tab0)
rownames(PopIlots) <- paste(rep("generation", gen), 1:gen, sep = "")
# Affichage du tableau des résultats
cat("\nLa dérive génétique a abouti à l'unique espèce :\n",
unique(ilot), "à la génération", gen, "\n\n")
print(PopIlots)
# Représentation graphique en segments de droites
plot(1:gen, PopIlots[ , unique(ilot)], type = "l", col = unique(ilot),
xlab = "Rang de la génération", ylab = "Effectif de l'espèce restante",
main = paste("Évolution de l'effectif de l'espèce", unique(ilot), "\npendant",
gen, "générations en début de génération"))
# Création des variables pour que plot fasse des boxplot, puis réalisation du graphique
# dev.new() # Si on est sous Tinn-R pour une nouvelle fenêtre
# Sous RStudio on peut faire défiler tous les graphiques faits
nLign <- dim(PopIlots)[1] ; nCol <- dim(PopIlots)[2]
y <- PopIlots[, 1] ; for (i in 2:nCol) y <- c(y, PopIlots[, i])
x <- as.factor(
rep(c("black", "blue","green", "red", "violet", "yellow"),
rep(nLign, nCol)))
plot(x, y,
main = paste(
"Distributions* simulées du nombre d'individus",
"\nen début de génération, espèce par espèce",
"\nEspèce restant seule =", unique(ilot)),
xlab = "Espèces", ylab = "Nombre d'individus",
border = levels(x))
}
> DerivEscar2_1()
La dérive génétique a abouti à l'unique espèce :
green à la génération 8
black blue green red violet yellow
generation1 2 3 2 4 6 3
generation2 1 6 4 2 4 2
generation3 0 10 2 6 10 0
generation4 0 0 5 11 1 0
generation5 0 0 2 19 0 0
generation6 0 0 6 15 0 0
generation7 0 0 16 5 0 0
generation8 0 0 6 0 0 0
Hubert RAYMONDAUD 07/12/12
LEGTA LOUIS GIRAUD *
84200 CARPENTRAS page 5 sur 11 DeriveEscargots.odt