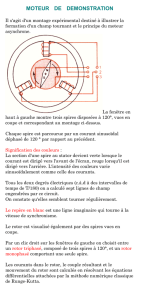
Influence de la Vitesse de Pré rotation sur le Comportement

___________________________________________________________________________________________________
9ième Congrès de Mécanique, FS Semlalia, Marrakech 82
Influence de la Vitesse de Pré rotation sur le Comportement Dynamique des Joints Lisses
Descendants de Turbomachines
M. KAMOUNI 1, M. SRITI 2
1 EST de Fès, Département Génie mécanique et
Productique, B.P.2427, Route d’Imouzzer, Fès, Maroc
E-Mail: [email protected]
2 FST-Errachidia, Labo. de Mécanique-Energétique,
Départ. de Physique, B.P.509, Boutalamine,
Errachidia, Maroc
E-Mail: [email protected]
Introduction :
Les joints annulaires sont des éléments mécaniques
intégrants de turbomachines. Ils sont intégrés aux
entrefers des machines tournantes pour assurer
l’étanchéité dynamique tout en évitant l’usure de
frottement entre le rotor et le stator. Cependant, leur
existence peut modifier les caractéristiques dynamiques
de la ligne d’arbre [1].
En vue de contribuer à l’amélioration des
performances des joints lisses descendants, le présent
travail se base sur un modèle de calcul global pour
analyser le comportement dynamique de ce type de joints
dans des conditions de fonctionnement variées. L’étude
porte, essentiellement, sur l’effet de la vitesse de pré
rotation win sur les coefficients dynamiques de ces joints.
Les figures 1 et 2 illustrent la géométrie du joint étudié et
le système de coordonnées utilisé.
Formulation et Méthode :
L’écoulement est supposé compressible, adiabatique et
pleinement turbulent. L’épaisseur du film est supposée
suffisamment mince pour négliger les forces de pesanteur et la
variation des grandeurs physiques dans la direction radiale. Le
gaz est supposé parfait. L’écoulement dans ces joints est
gouverné par l’équation de continuité, les équations de
conservation de la quantité de mouvement dans les directions
axiale et circonférentielle et l’équation de conservation de
l’énergie.
(1)
(2)
(3)
(4)
p, ρ et T sont respectivement la pression, la densité et la
température du fluide. u et w sont respectivement la vitesse
axiale et la vitesse circonférentielle de l’écoulement dans le
joint. h étant l’épaisseur locale du film. cv est la chaleur
spécifique à volume constant. fr et fs sont les coefficients des
contraintes de frottement pour un écoulement turbulent relatifs,
respectivement, au rotor et au stator. Ces coefficients sont
déduits du modèle de Hirs [2] pour les contraintes de
frottement visqueux relatives au rotor et au stator :
(5)
(6)
Dans la plupart des applications industrielles, l’effet de la
rugosité est pris en considération. Les coefficients de
frottement pour des parois rugueuses sont approchés par la
formulation de Moody [3] :
(7)
(8)
Figure 2 : Vue en coupe longitudinale d’un
joint lisse descendant
s
f
2
w
2
u
2
1
s
+=
ρτ
0=
z
hu)(
+
θ
hw)(
R
1
+
t)h( ∂
∂
∂
∂
∂
∂
ρ
ρ
ρ
( )
z
p
h-=
θR
w
+
z
u
u+
t
u
h+
f)R-(w+u
2uρ
+f)w+(u
2uρ
r
1/2
22
s
1/222
∂
∂
∂
u∂
∂
∂
∂
∂
ρ
ω
( )
θ
p
R
h
-=
θR
w
+
z
u+
t
h+
f)R-(w+u
2)R-ρ(w
+f)w+(u
2
ρw
r
1/2
22
s
1/222
∂
∂
∂
w∂
∂
w∂
∂
w∂
ρ
ω
ω
[ ]
2
w
+
2
u
+Tc=Eavec
0=f)R-(w+u
2)R-ρRω(w
+
R
1
+
z
+
22
v
r
1/2
22
ω
ωθ
ρ
ρ
ρ
∂
∂
∂
∂
∂
∂
)hwE()huE(
t)hE(
r
f
2
)Rw(
2
u
2
1
r
+=
ωρτ -
( )
3
1
2
1
22
5
4
s
w+uρh
µ5.10
+
h
10+10.001375=f
δ
( )
3
1
2
1
22
5
4
r
)R-(w+uρh
µ5.10
+
h
10+10.001375=f
ω
δ
Figure 1 : Vue en espace d’un joint lisse
descendant

___________________________________________________________________________________________________
9ième Congrès de Mécanique, FS Semlalia, Marrakech 83
où δ est la longueur caractéristique de la rugosité des parois
du rotor et du stator.
L’équation d’état pour un gaz parfait est introduite pour
éliminer la température dans l’équation de l’énergie.
(9)
où γ est le rapport de chaleur spécifique.
Pour des petits mouvements du centre du rotor par
rapport à sa position d’équilibre, les équations de
conservation sont linéarisées en fonction de l’excentricité
relative
ε [ε =2e/(Ce+Cs)<< 1, où e est l’excentricité du
rotor par rapport au stator]. Cette méthode de linéarisation
conduit à un système différentiel non linéaire en z
correspondant aux grandeurs moyennes (p0, ρ0, u0 et w0) de
l’écoulement et un système d’équations aux dérivées
partielles du premier ordre correspondant aux fluctuations
(p1, ρ1, u1 et w1) des mêmes grandeurs [4, 5]. Ces
fluctuations sont cherchées de la même forme harmonique
que celle de l’épaisseur locale du film. La résolution de ces
systèmes nécessite la satisfaction des conditions aux limites
qui découlent des équations de la pression d’arrêt pour un
écoulement isentropique à l’entrée du joint [6]. La vitesse de
pré rotation est une donnée indépendante. A la sortie, le joint
débouche dans l’atmosphère. Ensuite, Les forces de pression
exercées sur le rotor sont déterminées par intégration des
fluctuations de pression le long du joint et le long de la
circonférence.
Par ailleurs, la relation liant la force au déplacement, la
vitesse de déplacement et l’accélération est représentée par le
modèle dynamique linéaire [7] suivant :
(10)
où (K, k) et (C, c) sont, respectivement, les coefficients
direct et croisé de raideur et d’amortissement. M est le
coefficient direct de masse ajoutée.
(11)
(12)
Les coefficients dynamiques K, c et M peuvent être
obtenus par une régression du second ordre de la
composante radiale Fr(Ω) dans l’équation (11). Les
coefficients dynamiques C et k sont déterminés par une
régression linéaire de la composante tangentielle Ft(Ω)
dans l’équation (12).
Résultats et Discussions:
Comme dans la plupart des applications industrielles,
on suppose que le rotor décrit, dans le même sens de
rotation de l’arbre, une trajectoire circulaire autour de sa
position d’équilibre initiale.
Les conditions de
fonctionnement du joint sont regroupées dans le tableau 1.
Du point de vue stabilité dynamique, la force
tangentielle Ft est généralement considérée à l’origine du
mouvement orbital qui conduit à l’instabilité du rotor. Le
coefficient croisé de raideur k tend souvent à déstabiliser le
rotor et il peut être négatif ou positif suivant le signe de la
différence des vitesses tangentielles entre l’entrée et la
sortie du joint [8]. Le coefficient direct d’amortissement C
joue un rôle important sur la stabilité du rotor, il réduit
l’effet déstabilisant de la raideur croisée. La force radiale Fr
tend, généralement, à centrer le rotor et à réduire
l’excentricité dynamique. Cependant, elle a une faible
influence sur la stabilité du rotor. En conséquence, les
coefficients dynamiques qui contribuent à la force radiale
(raideur directe K, amortissement croisé c et masse ajoutée
M) ne jouent pas de rôle majeur sur la stabilité ou
l’instabilité du rotor. Pour résumer, la stabilité ou
l’instabilité du rotor dépend essentiellement des coefficients
croisé de raideur k et d’amortissement direct C. Par
conséquent, les résultats de ce travail portent,
principalement, sur l’effet de la vitesse de pré rotation sur
les coefficients de raideur croisée et d’amortissement direct.
La figure 4 représente l’effet du rapport win / Rω sur le
coefficient de raideur croisée k. Cette figure montre que la
raideur croisée croit presque proportionnellement avec
l’accroissement de la vitesse de pré-rotation. Ce résultat
concorde qualitativement avec les mesures expérimentales
Longueur totale du joint Lt
Longueur descendante Ld
Rayon du rotor R
Jeu radial à l’entrée Ce
Jeu radial à la sortie Cs
Pression amont Pe
Pression aval Ps
Viscosité dynamique µ
Facteur de perte ζ
Rugosité de la paroi δ
Vitesse de rotation angulaire ω
Vitesse de vibration du rotor Ω
Température T
Rapport. de chaleur spécifique γ
50.8 mm
40.64 mm
76.2 mm
0.381 mm
0.127 mm
3 bars
1 bar
18 10-6 Kg/m.s
0.1
0.813 10-6 m
10000 tr/min
10000 tr/min
300 °K
1.4
Figure 3: Diagramme des forces de pression et coefficients
dynamiques du joint pour une orbite elliptique
Tableau 1 : Géométrie et conditions opératoires du joint
T
v
c)1(
p-
γ
ρ
=
+
y
x
M0
0M
y
x
Cc-
cC
+
y
x
Kk-
kK
=
F
F
-y
x
2
MaΩcb--Ka=0)(t
x+==
Ω F
r
F
Ω
Cb-ka=)(
y
0tFF
t
=
=

___________________________________________________________________________________________________
9ième Congrès de Mécanique, FS Semlalia, Marrakech 84
et les prédictions obtenues par Childs et Scharrer [8] et
Nelson et al. [9] respectivement dans le cas des joints
labyrinthes et des joints à marche utilisés dans des
turbines à gaz. En outre, Le coefficient de raideur
croisée a un effet déstabilisant. Par conséquent, une
valeur minimale est souhaitable pour ce coefficient.
-0,50 -0,25 0,00 0,25 0,50
-0,2
-0,1
0,0
0,1
0,2
0,3
0,4
Coefficient de raideur croisée
k (kN / mm)
W
in
/ R ω
ωω
ω
La figure 5 représente le coefficient
d’amortissement direct C en fonction du rapport win / Rω.
Cette figure montre que ce coefficient est très légèrement
sensible à la variation de la vitesse de pré-rotation et les
valeurs les plus élevées de ce coefficient sont obtenues
pour des vitesses de pré rotation légèrement négatives.
De plus, l’amortissement direct a un effet stabilisant et
une valeur maximale est souhaitable pour ce coefficient.
-0,75 -0,50 -0,25 0,00 0,25 0,50 0,75
0,52
0,56
0,60
0,64
0,68
Coefficient d'amortissement direct
C (N S / mm)
W
in
/ R ω
ωω
ω
Conclusions :
La stabilité dynamique d’un joint lisse descendant
est influencée par la valeur et le signe de la vitesse de pré
rotation de l’écoulement à l’entrée du joint. La
configuration optimale pour les conditions opératoires ci-
dessus, est obtenue pour une vitesse de pré rotation
légèrement négative correspondante à un rapport win / Rω
compris entre -0.25et 0.
Références :
[1] D. W. Childs, Turbomachinery Rotordynamic,
Phenomena, Modelling and Analysis, J. Wiley & Sons,
New York, 1991.
[2] G. G. Hirs, “A Bulk Flow Theory for Turbulent in
Lubricant Films”, Journal of Lubrication Technology,
pp.137-146, 1973.
[3] L. Moody, Friction Factors for Pipe Flow, Transactions of
the ASME, Vol. 66, 671, 1944.
[4] M. Kamouni and M. Sriti, Rotor-dynamic Coefficients for
Partially Tapered Annular Seals for Compressible Flow,
AMSE Journal, Modelling B, Vol. 74, N° 1, pp. 1-14,
2005.
[5] M. Kamouni and M. Sriti, Rotor Speed and Inlet Swirl
Effects on Leakage and Rotordynamic Coefficients of
Tapered Annular Gas Seals, AMSE Journal, Modelling B,
Vol.76 , N°6 , pp. 1-14, 2007.
[6] M. Kamouni, Simulation Numérique du comportement
Statique et Dynamique des Joints Annulaires de
Turbomachines, Mémoire d’Habilitation Universitaire,
Faculté des Sciences et Techniques de Fès, Maroc, 20
Novembre 2007
[7] T. Staubli and M. Bissig, Numerically Calculated
Rotordynamic Coefficients of a Pump Rotor Side Space,
International Symposium on Stability Control and
Rotating Machinery (ISCORMA), South Lake Tahoe,
California, 2001.
[8] D. W. Childs and J. K. Scharrer, Experimental
Rotordynamic Coefficients Results for Teeth on Stator
Gas Labyrinth Seals, AMSE Trans. Journal of
Engineering for Gas and Turbines and Power, Vol. 108,
pp. 599-604, 1986
[9] C. Nelson, M. Dunn and J. Scharrer, Rotordynamic
Coefficients for Stepped Annular Gas Seals, Proceedings
of the Third International Conference on Transport
Phenomena and Dynamics of Rotating Machinery, Vol. 2
(Dynamics), pp.259-272, Homolulu, 1990.
Figure 4: Coefficient de raideur croisée k en
fonction du rapport de la vitesse de pré
rotation sur la vitesse de rotation (win/Rω)
Figure 5: Coefficient d’amortissement direct
C en fonction du rapport de la vitesse de pré
rotation sur la vitesse de rotation (win/Rω)