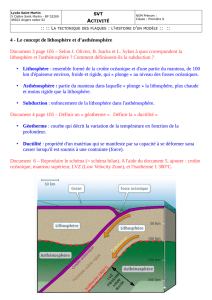
87Sr/86Sr

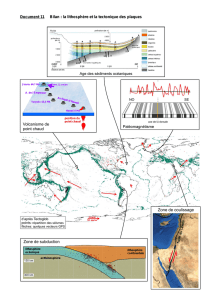
Constat de départ
La Terre est âgée de 4,55 Ga.
Cependant, les roches qui
affleurent en surface de la
lithosphère sont d’âges très
variés.
Carte des âges de la surface de la Terre (Extrait de S.V.T TS Nathan ed 2012)
Observations :
L’âge de la croûte océanique varie de 0 à 175 Ma
L’âge de la croûte continentale varie de 0 à 3,8 Ga
Problème : Comment estimer l’âge des roches crustales et
expliquer la différence observée entre océans et
continents ?
BILAN :
La croûte continentale date, par endroits, de
plus de 4 Ga.
En revanche, l’âge
n’excède pas 200 Ma.
de
la
croûte
océanique
Géologie
TP4 : LITHOSPHÈRES OCÉANIQUE ET
CONTINENTALE : DES ENVELOPPES D’ÂGES
DIFFÉRENTS
On voit que quand le temps passe les quantités de 87Rb et
varient.
On peut donc déterminer l’âge d’une roche grâce à
concentrations dans les différents minéraux qui la constituent.
87Sr
ces
Que peut-on dire du rapport initial
Le rapport initial
départ
87Sr/86Sr
Comment évolue le rapport
minéral considéré ?
87Sr/86Sr
des quatre types de minéraux ?
est identique dans les quatre minéraux au
87Sr/86Sr
par rapport au rapport
87Rb/86Sr
Quand le temps passe, 87Sr augmente  Le rapport
augmente
Alors que 87Rb diminue  Le rapport 87Rb/86Sr diminue
t
87Sr
pour chaque
87Sr/86Sr
87Rb


Quel facteur fait varier la pente de la droite obtenue ?
C’est le temps qui fait varier la pente de la droite obtenue
Pour déterminer le temps depuis lequel la roche a cristallisé, il suffit de calculer le
coefficient directeur de la droite obtenue.
Écrivez l’équation générale de la courbe obtenue.
L’équation générale de la courbe obtenue est celle d’une droite :
Y
(87Sr/86Sr)
=
B
=
(87Sr/86Sr)o
+
+
AX
t.(87Rb/86Sr)
donc t = A/
avec A = t
Calculez l’âge du granite d’Athis.
Document 1 : Concentrations des différents isotopes dans le granite d’Athis
Minéraux
87Rb
86Sr
87Sr
87Rb/86Sr
87Sr/86Sr
Orthose
109,07706
26,82378
19,88423
4,06643
0,74129
Plagioclase
2,73996
38,34619
27,20168
0,07145
0,70937
Mica noir
106,96398
2,12996
2,35670
50,21877
1,10645
Mica blanc
92,55280
3,11936
2,93385
29,67044
0,94053
Isochrone du granite d'Athis
1,2
f(x) = 0,0078985009x + 0,7084879886
1
87Sr/86Sr
0,8
0,6
0,4
0,2
0
0
10
20
30
87Rb/86Sr
40
50
60
RAPPEL :
Pente de la droite = ( yB – yA) / ( xB – xA )
Minéraux
87Rb
86Sr
87Sr
87Rb/86Sr
87Sr/86Sr
Orthose
109,07706
26,82378
19,88423
4,06643
0,74129
Plagioclase
2,73996
38,34619
27,20168
0,07145
0,70937
Mica noir
106,96398
2,12996
2,35670
50,21877
1,10645
Mica blanc
92,55280
3,11936
2,93385
29,67044
0,94053
Ici :
Pente de la droite = (1,10645-0,70937)/(50,21877-0,07145) = 0,00792
Or  = 1,42.10-11 an-1
Et Pente =  t
Donc t = Pente /  = 0,00792 / 1,42.10-11 = 559 Ma
BILAN :
L’âge des roches (ici de la croute continentale)
peut être déterminé par radiochronologie
On voit que plus le temps passe moins le flux thermique est élevé
 Ce qui signifie que la lithosphère est de plus en plus froide quand
elle vieillit.
Document 2 : Analyse des relevés de terrain « Océan Atlantique – 30° latitude Sud »
Axe
dorsale
Croûte d = 2,9
500°C
ec = 5 km
900°C
1300°C
d = 3,3
Asthénosphère
d =
3,25
Épaisseur lithosphère (km) :
0 2
Densité lithosphère :
13
d1
10 15
27 36
d2 d3
25 30
60
40
58
71
d4 d5
d6
d7
Age (Ma)
120
100
80
46 50
Lithosphère
82
92
d8
d9
Age de la lithosphère océanique en 106 années
2
10
15
25
30
40
60
80
100
Distance à l’axe de la dorsale en km
60
245
310
460
600
800
1200
1800
2225
croûte
5
5
5
5
5
5
5
5
5
manteau
8
22
31
41
45
53
66
77
87
13
27
36
46
50
58
71
82
92
Épaisseur de la
lithosphère océanique
(en km)
Épaisseur totale de la lithosphère océanique
(en km)
Densité LO
Exemple de calcul :
3,146 3,226 3,244 3,256
3,26
Densité à 2 Ma = [(5 x 2,90) + (8 x 3,30)] / 13 = 3,146
3,265 3,272 3,276 3,278
On voit que plus la lithosphère
océanique est âgée et froide,
plus elle est épaisse.
Cet épaississement se fait par
« ajout » de manteau ; la CO a
toujours la même épaisseur
On voit que plus la lithosphère
océanique est âgée, froide et
épaisse, plus elle est dense.
On voit que plus la lithosphère océanique est âgée, froide, épaisse et
dense, plus elle s’enfonce.
BILAN :
En s’éloignant de la dorsale, la lithosphère
océanique, de plus en plus vieille, se refroidit,
s’épaissit et devient plus dense, donc s’enfonce.
Age de la lithosphère océanique en 106 années
2
10
15
25
30
40
60
80
100
Distance à l’axe de la dorsale en km
60
245
310
460
600
800
1200
1800
2225
croûte
5
5
5
5
5
5
5
5
5
manteau
8
22
31
41
45
53
66
77
87
13
27
36
46
50
58
71
82
92
Épaisseur de la
lithosphère océanique, (en
km)
Épaisseur totale de la lithosphère océanique
(en km)
Densité LO
3,146 3,226 3,244 3,256
3,26
3,265 3,272 3,276 3,278
La lithosphère est en équilibre sur l’asthénosphère tant que sa
densité est inférieure à celle de l’asthénosphère.
Si la densité de la lithosphère devient supérieure, elle peut
littéralement plonger sous l’asthénosphère car l’équilibre est rompu.
La densité de l’asthénosphère est de 3,25.
La lithosphère peut donc plonger sous l’asthénosphère entre 15 et
25 Ma.
Or, on retrouve des LO datée de plus de 25 Ma (jusqu’à 200 Ma !).
Qu’est ce qui permet d’expliquer ce phénomène ?
La LO pourrait théoriquement plonger à partir de 20 Ma mais
l’asthénosphère exerce une résistance mécanique à son
enfoncement.
 La LO ne plonge donc que des millions d’années plus tard.
BILAN :
En s’éloignant de la dorsale, la lithosphère
océanique, de plus en plus vieille, se refroidit,
s’épaissit et devient plus dense donc s’enfonce.
L’augmentation de sa densité au-delà d’un seuil
d’équilibre
explique
son
plongement
dans
l’asthénosphère.
La différence de densité entre l’asthénosphère
et la lithosphère océanique âgée est la principale
cause de la subduction.
En surface, son âge n’excède pas 200 Ma.