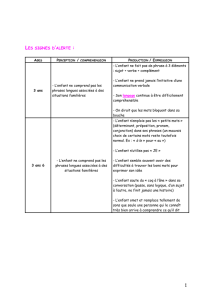
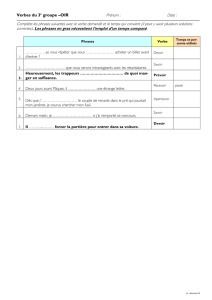
Logique - Chez Laurent Roussarie

Logique
Résumé 1er cours
1 L’objet de la logique
Objet de la logique = les raisonnements ; et plus précisément ce qu’on appelle les schémas
argumentatifs ou formes de raisonnement ou encore schémas d’inférences.
Exemple :
(1) Tous les hommes sont mortels
Socrate est un homme
Socrate est mortel
Notation 1 (Schéma argumentatif)
Un schéma argumentatif se notera de la manière suivante, où p1, p2,...,pnsont, ou représentent,
des phrases déclaratives :
p1
p2
.
.
.
pn−1
pn
A plat, on écrira: p1, p2,...,pn−1/pn.
Les phrases p1, p2,...,pn−1s’appellent les prémisses du schéma argumentatif, et pnsa
conclusion.
Autres exemples :
(2) S’il pleut, je reste chez moi
Il pleut
Je reste chez moi
(3) Aucun rossignol ne sait jouer de la guitare
Serge sait jouer de la guitare
Serge n’est pas un rossignol
(4) Le coupable est soit un chameau, soit un dromadaire
Le coupable n’est pas un dromadaire
Le coupable est un chameau
Remarques: En logique standard, l’ordre des prémisses entre elles n’a aucune importance. De
plus, le nombre de prémisses dans un schéma argumentatif est tout à fait quelconque : on peut
avoir une seule prémisse, comme en (5), et même aucune, comme en (6).
(5) Je pense
Je suis
(6) En ce moment, soit il pleut, soit il ne pleut pas
2 Validité vs. vérité
Les raisonnements suivants (7–9) sont logiquement « incorrects », car il manque une relation
de conséquence logique entre les prémisses et la conclusion. On dira qu’ils sont non valides.
(7) Tous les hommes sont mortels
Rantanplan est mortel
Rantanplan est un homme
(8) S’il y a de la glace en dessert, j’en prends
Il y a de la glace en dessert
Je n’en prends pas
1

(9) Il y a (= il existe) des pharmaciens
Il y a des pharmaciens chauves
Tous les pharmaciens sont chauves
Le but de la logique est de faire le tri entre les raisonnments valides et ceux qui ne le sont pas.
En d’autres termes, la logique porte des jugements d’acceptabilité sur les formes de raisonnement.
Définition 1 (Validité)
Un schéma argumentatif valide est tel que lorsque ses prémisses sont vraies, alors sa conclusion
doit toujours être vraie aussi.
Important : il ne suffit pas que les prémisses et la conclusion se trouvent être vraies ensembles
pour qu’un raisonnement soit valide.
(10) La pintade est un galinacé
L’eau bout à 100˚C
Elizabeth II est la Reine d’Angleterre
Il faut que la conclusion soit vraie dans tous les cas de figures où les prémisses sont vraies
pour qu’un raisonnement soit valide.
La vérité factuelle des prémisses et de la conclusion n’a pas d’importance ; seule compte la
vérité relative de la conclusion par rapport aux prémisses. Ainsi (11) est valide, même si les
phrases qui le composent sont fausses dans notre réalité :
(11) Les girafes sont imbattables aux échecs
Lady Gaga est une girafe
Lady Gaga est imbattable aux échecs
En revanche (12) n’est pas valide, bien que ses prémisses et sa conclusion soient vraies par
rapport à la réalité zoologique. Mais la conclusion n’est pas une conséquence des prémisses.
(12) Tous les bovins sont des ruminants
Le cheval n’est pas un bovin
Le cheval n’est pas un ruminant
3 Logique formelle et symbolique
On a même pas besoin de comprendre tout le sens des phrases qui composent un raisonnement
pour juger s’il est valide ou non :
(13) Si un borogove bournifle sur l’alloinde, il galomphe
Les verchons sont des borogoves qui bourniflent sur l’alloinde
Les verchons galomphent
Seule compte la compréhension de la structure syntaxique/sémantique des phrases, c’est-à-dire
le sens de mots comme si,un,le(s),tous, etc. Ces éléments fondent la configuration structurelle
des phrases, ce que l’on appellera ici la forme des phrases. C’est pourquoi on parle de logique
formelle.
C’est parce que (13) est de la forme (14) que l’on sait qu’il est valide.
(14) Si un A B, (alors) il C
Les Dsont des Aqui B
Les D C
où Aet Dreprésentent des noms et Bet Cdes groupes verbaux.
De même, (1) est valide, car il est de la forme :
(15) Tous les Asont B
Cest un A
Cest B
2

Voici quelques autres schémas d’inférence généraux et valides.
Modus ponens:
Si A, (alors) B
A
B
Remplacez Aet Bpar n’importe quelles phrases déclaratives, vous obtiendrez un raisonne-
ment valide (cf. (2).
Modus tollens:
Si A, (alors) B
Non B
Non A
Ici, Non Bet Non Areprésente les tournures négatives des phrases Bet A. Le schéma (16)
est un exemple de modus tollens.
(16) Si Pinocchio ment, son nez s’allonge
Le nez de Pinocchio ne s’allonge pas
Pinocchio ne ment pas
Mais attention ! la forme de raisonnement suivante, elle, n’est absolument pas valide :
(17) Si A, (alors) B
Non A
Non B
Par exemple, (18) n’est pas valide :
(18) Si les taux d’intérêt augmentent, la bourse baisse
Les taux d’intérêt n’augmentent pas
La bourse ne baisse pas
En revanche le schéma suivant, que l’on appelle le dilemme bivallent, est valide (exemple en (20)) :
(19) Si A, (alors) B
Si non A, (alors) B
B
(20) Si je tue le Comte, je perds l’amour de Chimène
Si je ne tue pas le Comte, je perds l’amour de Chimène
Je perds l’amour de Chimène
Voici encore un autre schéma d’inférence valide (cf. (4)) :
(21) Aou B
Non A
B
Récapitulatif
C’est la forme des énoncés composant les raisonnements qui compte ; il est donc dans notre
intérêt de travailler directement sur des formulations générales et plutôt abstraites comme si A,
(alors) B,non A,Aou B, etc... Cela nous permet en effet de capter des réguralités sur les pro-
priétés logiques des raisonnements, sans avoir à examiner des multitudes d’instances particulières
formulées en langage naturel. Ces notations générales sont déjà symboliques, car elles utilisent
des variables (donc des symboles qui n’appartiennent pas à la langue française) A,B,C... qui
valent pour n’importe quelle phrase déclarative. Mais on va aller encore plus loin dans ce sens. En
plus d’être formelle, la logique que nous étudions est symbolique. Cela signifie que les raisonne-
ments sur lesquels nous allons travailler vont être entièrement traduits dans un langage artificiel
3

(on dit aussi parfois formel), abstrait, de type mathématique, c’est-à-dire symbolique. Cela aura
aussi pour intérêt de nous débarrasser de toute l’ambiguïté inhérente aux langues naturelles. En
logique les formulations sont précises et non polysémiques.
4