énoncé - Chimie

JM Urbain – Janson de Sailly
1
DS5
PCSI option SI et PCSI7 option Chimie – Calculatrice autorisée
Problème 1
Modèles de pharmacocinétique
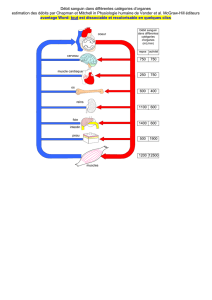
La pharmacocinétique est l’étude du devenir d’un médicament dans l’organisme. Après son
administration, le principe actif franchit différentes barrières pour finalement accéder au plasma
sanguin. La circulation sanguine assure sa distribution dans l’organisme. Il peut alors parvenir à son
site d’action, ou être métabolisé (c’est-à-dire transformé) puis éliminé ou encore être stocké. Sa
concentration dans le plasma sanguin évolue donc au cours du temps. Les études pharmacocinétiques
font partie du cahier des charges dans le développement de tout nouveau médicament.
Après l’administration d’un médicament, la mesure de sa concentration dans le plasma
sanguin est en général possible, ce qui permet de suivre son évolution au cours du temps.
Cette évolution a été suivie pour l’acide valproïque, de formule topologique représentée ci-
dessous, médicament antiépileptique commercialisé sous le nom de Dépakine®.
CO2H
figure 1 - acide valproïque
La figure 2 présente l’évolution temporelle de la concentration massique 𝐶 de cette molécule
dans le plasma sanguin d’un patient à qui on a administré une masse 𝐷 = 2,0 𝑔 (appelée
« dose ») d’acide valproïque de deux manières différentes : par injection intraveineuse
(forme a) ou par administration par voie orale d’une forme galénique dite « à libération
prolongée » (forme b).
figure 2 – concentration massique du médicament dans le plasma sanguin en fonction du mode
d’administration : par intraveineuse (a) ou par voie orale (b)

JM Urbain – Janson de Sailly
2
1) Sachant que les taux thérapeutiques recommandés pour cette molécule sont situés entre
𝟒𝟎 𝒆𝒕 𝟏𝟎𝟎 𝒎𝒈.𝑳!𝟏 (intervalle dit « thérapeutique », entre le seuil thérapeutique et le
seuil de toxicité), commenter et comparer très succinctement les résultats des deux
modes d’administration.
On se propose d’étudier deux modèles pharmacocinétiques simples pour justifier l’évolution temporelle
de la concentration massique C de l’acide valproïque dans le plasma sanguin en fonction du mode
d’administration choisi (a ou b).
1. Modèle pour l’administration intraveineuse (forme a)
La dose (masse 𝐷 = 2,0 𝑔) est directement injectée dans le plasma sanguin à la date t = 0.
On note 𝑪𝟎 la concentration massique initiale d’acide valproïque dans le plasma sanguin et
𝑪 la concentration massique d’acide valproïque dans le plasma sanguin à l’instant 𝑡.
La disparition du médicament dans le plasma est modélisée par une cinétique d’ordre 1 (par
rapport au médicament dans le plasma), de constante de vitesse 𝑘! comme indiqué sur le
schéma ci-dessous :
−
𝒅𝑪
𝒅𝒕 =𝒌𝒆𝑪
2) Déterminer par résolution de l’équation différentielle l’expression de 𝑪 en fonction du
temps t.
3) Exploiter les résultats du tableau ci-dessous donnant la concentration massique 𝑪 dans
le plasma sanguin à différentes dates pour d’une part vérifier l’adéquation des résultats
au modèle et d’autre part déterminer les valeurs de 𝒌𝒆 et de la concentration massique
initiale 𝑪𝟎. La méthode choisie et les différents calculs devront être très soigneusement
présentés.
temps t / h
0,08
4,0
8,0
16,0
32,0
48,0
64,0
80,0
96,0
C / mg.L–1
155
140
120
80
40
20
10
5,0
2,5
Tableau 1
(Les valeurs du tableau sont issues de la courbe a de la figure 2)
Lorsque la dose est administrée à la date t = 0, elle est dissoute dans une partie de
l’organisme que l’on assimile à une solution de volume 𝑽𝒅 appelé volume de distribution.
4) Déduire des résultats la valeur du volume de distribution.
C!t"
#$%&'%(&%)*+,)
-.$+'/#V0
k/

JM Urbain – Janson de Sailly
3
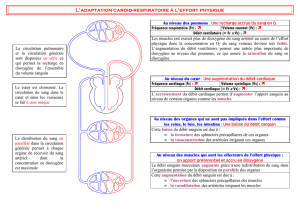
2. Modèle pour l’administration par voie orale (per os)
La dose d’acide valproïque, de masse D, administrée en une fois par voie orale doit parvenir
dans le plasma sanguin par échanges tout au long du tube digestif (au niveau de l’estomac et
de l’intestin en particulier).
L’absorption et la consommation par l’organisme du médicament sont modélisées par des
lois cinétiques d’ordre 1 et de constantes de vitesse respectives 𝑘! et 𝑘!, avec 𝑘!≠𝑘!.
On note respectivement 𝑚!(𝑡) et 𝑚!(𝑡) les masses d’acide valproïque dans le tube digestif
(indice T) et dans le plasma sanguin (indice P).
5) Compte-tenu de la modélisation proposée, établir le système d’équations différentielles
vérifié par 𝒎𝑻(𝒕) et 𝒎𝑷(𝒕).
6) En déduire l’expression de la masse 𝒎𝑻(𝒕) au niveau du tube digestif en fonction du
temps et des paramètres jugés utiles.
7) La résolution du système d’équations différentielles donne également :
𝒎𝑷𝒕=
𝒌𝒂
𝒌𝒂−𝒌𝒆
×𝑫×𝒆!𝒌𝒆𝒕−𝒆!𝒌𝒂𝒕
En déduire l’expression de 𝑪(𝒕), concentration massique de l’acide valproïque dans le
plasma sanguin, en introduisant le volume de distribution 𝑽𝒅 supposé identique à celui
déterminé précédemment (partie 1.1).
8) Montrer que 𝑪(𝒕) passe par un maximum noté 𝑪𝒎𝒂𝒙 à une date notée 𝒕𝒎𝒂𝒙. Exprimer
𝒕𝒎𝒂𝒙 en fonction de 𝒌𝒆 et 𝒌𝒂.
9) Montrer que : 𝑪𝒎𝒂𝒙 =𝑫
𝑽𝒅
×𝒆!𝒌𝒆𝒕𝒎𝒂𝒙 .
10) A l’aide de la figure 2, évaluer graphiquement les valeurs de 𝒕𝒎𝒂𝒙 et 𝑪𝒎𝒂𝒙.
11) En déduire la valeur de 𝒌𝒆 (on conservera la valeur de 𝑽𝒅 trouvée dans la partie 1.1). Par
résolution à la calculatrice en déduire ensuite la valeur de 𝒌𝒂.
mT(t)
tube
digestif
kamP(t)
plasma2sanguin
volume$Vd
ke

JM Urbain – Janson de Sailly
4
Problème 2
Traitement des intoxications au monoxyde de carbone
Le monoxyde de carbone est un gaz inodore et incolore, très toxique car la molécule peut se lier à
l’hémoglobine 𝐻𝑏 et prendre la place du dioxygène pour former la carboxyhémoglobine notée 𝐻𝑏𝐶𝑂.
L’oxygénothérapie hyperbare est utilisée pour traiter les intoxications au monoxyde de
carbone. Il s’agit de faire respirer au patient intoxiqué de l’oxygène pur sous une pression
supérieure à 1 bar. Le traitement peut être modélisé par la réaction d’équation :
𝑯𝒃𝑪𝑶 (𝒂𝒒) + 𝑶𝟐 (𝒈) = 𝑯𝒃(𝑶𝟐) (𝒂𝒒) + 𝑪𝑶 (𝒈)
Une étude a été réalisée sur une dizaine de patients. Dans chaque expérience la pression en
dioxygène inspiré est maintenue constante.
L’évolution de la concentration en carboxyhémoglobine, a été suivie au cours du temps afin
d’étudier la cinétique de la réaction d’équation ; on suppose que la loi de vitesse peut se
mettre sous la forme :
𝒗𝒓é𝒂𝒄𝒕𝒊𝒐𝒏 = 𝒌·[𝑯𝒃𝑪𝑶]𝒂·(𝒑(𝑶𝟐))𝒃
La courbe ci-dessous montre le résultat expérimental obtenu pour une pression en dioxygène
inspiré constante et égale à 𝒑(𝑶𝟐)=𝟐,𝟎 𝒃𝒂𝒓.
L’expérience a été répétée pour différentes pressions en dioxygène, toujours maintenues
constantes au cours de l’expérience. Le tableau ci-dessous rassemble les valeurs de temps de
demi-réaction 𝒕𝟏/𝟐 obtenus pour différentes pressions 𝒑(𝑶𝟐) en dioxygène :
𝑝(𝑂!) / bar
0,2
1,0
1,5
2,5
𝑡!/! / min
250
50
33
20
12) Proposer un schéma de Lewis pour la molécule de monoxyde de carbone 𝑪𝑶.
13) Donner la définition du temps de demi-réaction 𝒕𝟏/𝟐 pour cette réaction.
14) Déterminer graphiquement pour l’expérience effectuée avec 𝒑(𝑶𝟐)=𝟐,𝟎 𝒃𝒂𝒓 la valeur
de 𝒕𝟏/𝟐.
15) Exploiter les résultats expérimentaux pour déterminer les ordres partiels α et β. Le
raisonnement devra être très clairement présenté.
0"
5"
10"
15"
20"
25"
30"
35"
0" 10" 20" 30" 40" 50" 60" 70"
proportion'de'
HbCO'(en'%)'
temps/min'