formula théorème -fait

!"#$%&'('")*+,$%&'-''
./%'/01%234/,5&6'
'
7)8/5,&'+9323,5&'1&'23':,;53#/0'2%<,0&%+&'
=)80/<>0&+'1?,04&5@85&09&+'
A)3",45&'!=BC'
'
Les$condi*ons$d’interférences$
Mise$en$évidence$expérimentale$$
sur$des$ondes$mécaniques$de$faible$fréquence!
D89&++,48'1&'2?311,#:,48E'1%'+*09)5/0,+<&'&4'1&'23'9/)85&09&!

La$théorie$de$la$vibra*on$scalaire$
Les$limites$de$l’op*que$géométrique'
F?/"#$%&'G8/<845,$%&'5&"/+&'+%5''23'0/#/0'@/013<&0432&'1&'rayon$lumineux$:$
Lieu$des$points$de$l’espace$correspondant$à$une$trajectoire$possible$de$la$lumière$
$
.2&'9/%5+'1&'"5&<,>5&'3008&'"/+4%2&'une$propaga*on$en$ligne$droite$130+'%0'<,2,&%'
)/</G>0&'4530+"35&04E'le$principe$du$retour$inverse$$&4'les$lois$de$SnellBDescartes$H'
2?,04&5@39&'1?%0'1,/"45&'&4'1?%0'<,5/,56'
'
B F&+'53*/0+'2%<,0&%I'+/04'+%""/+8+',018"&01304+'&045&'&%I'
B F3'<359)&'1&+'53*/0+'2%<,0&%I'2/5+'1&'58J&I,/0+'&4'58@539#/0+'+%99&++,:&+'.1/008&'
&I394&<&04'"35'2&+'2/,+'1&'K&+9354&+6'&+4'/;4&0%&'"/%5'1&+'+*+4><&+'/"#$%&+'
9&0458+''.et$dans$les$condi*ons$de$GAUSS)$"35'1&+'45398+'1&'+&G<&04+'5&9#2,G0&+'
%#2,+304'1&+'828<&04+'9351,03%I'."230+'@/93%IE'"230+''"5,09,"3%IE'"/,04+'0/13%IL6'
B F&+'9/01,#/0+'089&++3,5&+'1&'@/5<3#/0'1&+',<3G&+'130+'1&+'"230+'1&'@5/04'+/04'2&'
s*gma*sme'&4'l’aplané*sme'.:85,M8&+'1&'@3N/0'3""5/9)8&'130+'2&+'9/01,#/0+'1&'
O3%++6'
La$théorie$de$la$vibra*on$scalaire$
Les$limites$de$l’op*que$géométrique'
P0'@3,+9&3%'9*2,015,$%&'.53*/0'FQRST'"35'&I&<"2&6'1/00&'%0&'5&"58+&043#/0',0485&++304&'
1&'9&U&'0/#/0'1&'53*/0'2%<,0&%IV'W2'+?3G,4'32/5+'1?,+/2&5'."35'23'"&0+8&6'23'"%,++309&'
2%<,0&%+&':8),9%28&'130+'9&'45/0N/0'1?/01&'82&945/<3G08#$%&'"230&'1&'+&9#/0'M0,&'RV'
''
F3'"%,++309&'2/932&'"35'%0,48'1&'+&9#/0'0/5<32&'&+4'1/008&'"35'23'0/5<&'1%':&94&%5'1&'
=/*0#0G'</*&0'&4'23'1,5&9#/0'&4'2&'+&0+'1&'"5/"3G3#/0'1&'23'2%<,>5&'"35'9&22&+'1&'9&'
:&94&%5V'
X823+E'+,'/0'9)&59)&'H',+/2&5'%0'@3,+9&3%'9*2,015,$%&'1&'+&9#/0'23'"2%+'@3,;2&'"/++,;2&E'2&+'
2/,+''1&'2?/"#$%&'G8/<845,$%&':/04'Y45&'<,+&+'H'<32'"35'le$phénomène$de$diffrac*on'
1/04'2&+'&Z&4+'+&5/04'1?3%4304'"2%+',<"/54304+'$%&'23'1,<&0+,/0'4530+:&5+32&'1%'@3,+9&3%'
+&'53""5/9)&53'1&'23'2/0G%&%5'1?/01&'1&'23'2%<,>5&'</0/9)5/<3#$%&V'

La$théorie$de$la$vibra*on$scalaire$
Les$limites$de$l’op*que$géométrique'
F3'58+/2%#/0'1&+'8$%3#/0+'1&'[3I\&22'130+'2&':,1&'/%'130+'%0'<,2,&%'4530+"35&04'
)/</G>0&'&4',+4/45/"&'@/%50,4'"/%5'2&+'9/<"/+304&+'S'&4']'1%'9)3<"'%0&'@/5<&'G808532&'
1&'solu*on$par*culière$élémentaire$2?!01&'=230&'=5/G5&++,:&'X35</0,$%&'.=/235,+8&'
S22,"#$%&<&046'OPPHpe$$"#$%&'()*!+*,-!
'
F&'"5,09,"&'1&'+%"&5"/+,#/0'+?3""2,$%&'3%I'9)3<"+'82&945/<3G08#$%&+'.&4'0/0'3%'
:&94&%5'1&'=/*0#0G'^6''_'G5301&%5+':&94/5,&22&+'$%,'+?3`/%4&04'&0'%0'"/,04'1/008'1&'
2?&+"39&'&4'H'%0',0+4304'4V'F&+'&I"85,&09&+'<&U304'&0'8:,1&09&'2&+'phénomènes$
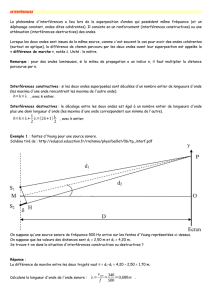
d’interférences$089&++,4&04'1&'9/003,45&'l’amplitude'&4'la$phase$instantanée$et$locale$1&'
23'G5301&%5':,;534/,5&'$%&'2?/0'9)/,+,53'"/%5'23'1&+95,"#/0'1&'2?/01&'2%<,0&%+&V'
'
!0'0&'"/%553',G0/5&5'2&'935394>5&':&94/5,&2'$%&'130+'1&%I'+,4%3#/0+'_'
B Ondes$polarisées$rec*lignement$quasi$parallèles$et$de$même$plan$de$polarisa*on$
B Ondes$de$polarisa*on$aléatoire$(nonBpolarisées)$:$succession$de$mul*ples$trains$
d’ondes$sur$la$durée$de$détec*on.$
!0'3""&22&''''''''''2&':&94&%5'1?/01&'2/932''
k( r)
s( r,t)=s( r).cos( ω .t− k( r). r)=s( r).cos( ω .t− ϕ ( r))
!0'"/+&53'32/5+'9&U&'18M0,#/0'1&'2?3<"2,4%1&'+9323,5&'1?%0&'/01&'2%<,0&%+&'</0/9)5/<3#$%&'
La$théorie$de$la$vibra*on$scalaire$
Le$théorème$de$MalusBDupin$'
.*!($/0)1,*!&*),*(!2*!)*&/)*)!30#%3*,*4(!3%!50),*!2*6!67)5%#*6!/87'&$%6*6!"67)5%#*6!
29042*-!'667*6!2974*!6*73*!607)#*:!)*3%;<*,*4(!=!3%!2')*#;04!2*6!>!)%?046!@!37,'4*7AB!
P0&',04&5"5843#/0'"/++,;2&'1&'9&'4)8/5><&'9/0+,+4&'H'1,5&'$%&'2?/0'08G2,G&'2&'5a2&'1&'23'
:35,3#/0'1&'1,5&9#/0'1%':&94&%5'1?/01&''+%5'%0'18"239&<&04',0M0,48+,<32'15'.</1>2&'
1?%0&'/01&'$%3+,B"230&'.2/932&<&04'"230&66'
d ϕ = r.d k+ k.d r=grad ( ϕ ( r)).d r≈ k.d r⇒grad ( ϕ ( r)) = k
+/,4'1&+'+%5@39&+'8$%,")3+&+'"&5"&01,9%23,5&+'3%':&94&%5'1?/01&'&4'1/09'3%'53*/0'2%<,0&%I'''
S0/098':"«"Après"un"nombre"quelconque"de"réflexions"ou"de"
réfrac9ons,"les"rayons"lumineux"issus"d’une"source"ponctuelle"sont"
normaux"aux"surfaces"d’onde"»"

La$théorie$de$la$vibra*on$scalaire$
Le$principe$de$FERMAT!
S0/098'C':"«"La"lumière"se"propage"d'un"point"à"un"autre"sur"des"trajectoires"
telles"que"la"durée"du"parcours"soit"extrémale"»"
=/%54304'/0'"58+&04&'+/%:&04'%0'"5,09,"&':35,3#/00&2'9/<<&'@/01&<&04'1&'2?/"#$%&'
G8/<845,$%&E'%0'"5,09,"&'1&'+43#/0035,48'$%,'"&5<&4'1&'5&45/%:&5'23'"5/"3G3#/0'
5&9#2,G0&E'2&'5&4/%5',0:&5+&'&4'2&+'2/,+'1&'R0&22BK&+9354&+V'S0'"35#9%2,&5E'+3'@/5<%23#/0'
@3,+304',04&5:&0,5'%0'"/,04'1&'18"354'&4'%0'"/,04'1?355,:8&E',2'+&'"5Y4&';,&0'H'2?84%1&'1%'
+#G<3#+<&'&4'1/09'1&'23'@/5<3#/0'1&+',<3G&+'_'
b%?&+4B9&'$%?%0'9)&<,0'/"#$%&'c'
S0/098'd':"«"Le"trajet"effec9vement"choisi"par"la"lumière"pour"aller"d’un"point"A"
à"un"point"B"correspond"à"une"valeur"sta9onnaire"du"chemin"op9que"par"
rapport"aux"trajets"fic9fs"voisins"allant"de"A"à"B"»"
b%?&+4B9&'$%?%0'9)&<,0'/"#$%&'+43#/003,5&'c'
La$théorie$de$la$vibra*on$scalaire$
Le$chemin$op*que!
b%?&+4B9&'$%?%0'9)&<,0'/"#$%&'c'
b%&'1,4'2&'"5,09,"&'1&'e&5<34'c'
F&'9)&<,0'/"#$%&'1&'Q'H']'2&'2/0G'1%'9/04/%5'!'&+4'2?,048G532&'_'''
AB
( )
≡n.dl
A
B
∫
AB
( )
≡n(M).dl
A
B
∫ = c
v
ϕ
.dl
A
B
∫=cdt
t1
t2
∫
soit$la$distance$parcourue$dans$le$vide$pendant$la$même$durée$
C0'(!74!#$*,'4!!9!<0'6'4!27!#$*,'4!!!!&)'6!&%)!3%!37,'1)*!
*(!6'!04!40(*!2D9,%A!!!3*!,%E0)%4(!2*6!/#%)(6!2*!&06';04:!
3*!#$*,'4!!!*6(!6(%;044%')*!6'!3%!<%)'%;04!2*!#$*,'4!
0&;87*!2"FG-!H!"FG-9I"FG-!%660#'/*!*6(!74!'4J4',*4(!&*;(!
27!6*#042!0)2)*!&%)!)%&&0)(!=!2D9,%A!

La$théorie$de$la$vibra*on$scalaire$
Le$chemin$op*que!
A&U&'5&9)&59)&'1%'9)&<,0'+43#/003,5&'"&%4'Y45&'3""2,$%8&'H'23'58@539#/0'+%5'%0'
1,/"45&'"/%5'5&45/%:&5'"35'&I&<"2&'23'45/,+,><&'2/,'1&'K&+9354&+'_'
A/0+,185/0+'f'9/<<&'%0'"/,04'1&'"/+,#/0'
:35,3;2&'+%5'2&'1,/"45&'&4'9)&59)/0+'23'
"/+,#/0'$%,'300%2&53'23':35,3#/0'3%'
"5&<,&5'/515&'1%'9)&<,0'/"#$%&'1.Q]6'
AB
( )
=AK
( )
+KB
( )
=n1.AK +n2.KB
d AB
( )
=n1.d AK
( )
+n2.d KB
( )
=n1. u1.dOK −n2. u2.dOK =0
avec O un point fixe du dioptre
soit un vecteur n1. u1−n2. u2 perpendiculaire au dioptre
et que l'on peut projeter sur la tangente en : n1.sin(i
1)=n2.sin(i2)
Remarques : !KI!+4!&*7(!2/,04()*)!#*L*!)*3%;04!*4!,'4','6%4(!3*!(*,&6!2*!&%)#07)6!&07)!! !
!!!!!!!!!!!!!!!!!!!!!!)*E0'42)*!74!!&0'4(!G!2*&7'6!74!&0'4(!F!%<*#!2*7A!<'(*66*6!2*!&)0&%M%;04!<K!*(!<NB!
!!!!"OP!27!6%7<*(*7)-!
!!!!NI+4!>!0P;*4(!@!/M%3*,*4(!#*L*!30'!2*!3%!)/5)%#;04!*4!&06%4(!3*!&)0P31,*!27!
!!!!&%66%M*!2974*!()07&*!)%4M/*!2974!603!27)!=!74!,%)/#%M*!Q!3%!2')*#;04!2*! ! !
!!!!!!!!!!!!!!!!!!!!!!2/&3%#*,*4(!/(%4(!2/J4'*!&*)&*42'#73%')*!%7A!)%4M6!HR!DFSTC!
La$théorie$de$la$vibra*on$scalaire$
Chemin$op*que$et$surfaces$d’onde!
T&45/%:/0+'2?8$%,:32&09&'&045&'=5,09,"&'1&'e&5<34'&4'7)8/5><&'1&'[32%+'"35'23'
5&23#/0'&045&'9)&<,0'/"#$%&'&4'+%5@39&+'1?/01&+V'
Une$surface$d’onde$est$le$lieu$des$points$M$tels$que$le$chemin$op*que$(SM)$
compté$le$long$d’un$rayon$lumineux$depuis$la$source$ponctuelle$S$soit$constant.$
R,'[C'&4'[d'+/04'1&%I'"/,04+',0M0,<&04':/,+,0+'1?%0&'<Y<&'+%5@39&'1?/01&'_''
''''''.RQQ?[C6g.R]]?[d6'
'
R,'2&'9)&<,0'.RQQ?[C6'&+4'+43#/003,5&'.eST[Q76E'32/5+'.R]]?[C6'0?&0'1,Z>5&'$%?H'2?/515&'d'
&0'Q]'&4'Q?]?'+/,4'3%'+&9/01'/515&'"5>+'_'.RQQ?[C6'g.R]]?[C6'
'
!5'23'1,Z85&09&'H'2?/515&'C'&045&'.R]]?[C6'&4'.R]]?[d6'+?895,4'_'u1.M1M2$/%'u2.M1M2$'
''''+/,4'
''
u1.M1M2 =0⇒rayon lumineux ⊥ surface d'onde