Chapitre 8 – Parallélogrammes - g

Chapitre 8 – Parallélogrammes
I. Le parallélogramme
1. Activité
Activité 1 : Construction d'un parallélogramme→
2. Définition
Définition : Un parallélogramme est un quadrilatère dont les côtés opposés sont parallèles.
Exemple : avec les carreaux
(AB) // (DC) et (AD) // (BC)
+ Notation : Donner tous les noms possibles du
parallélogramme tracé
3. Propriétés d'un parallélogramme
Propriété : Un parallélogramme admet un centre de symétrie qui est le point d'intersection de ses
diagonales.
Exemple :
I est le centre de symétrie de ABCD.
Propriétés : Si un quadrilatère est un parallélogramme alors,
- ses diagonales ont même milieu.
- ses côtés opposés ont même longueur.
- ses angles opposés sont égaux.
Démonstration :
Le point d'intersection I des diagonales est le centre de symétrie du parallélogramme ABCD.
Donc A et C sont symétriques par rapport à I et B et D sont symétriques par rapport à I.
Donc I est le milieu de [AC] et aussi le milieu de [BD].
Donc les diagonales de ABCD ont le même milieu, le point I.
La symétrie centrale conserve les longueurs donc AB = DC et AD = BC.
Les angles
ABC
et
CDA
sont symétriques par rapport à I et les angles
DAB
et
BCD
aussi.
Or la symétrie centrale conserve les mesures d'angles. Donc
ABC
=
CDA
et
DAB
=
BCD
.
Exemple :
Dans le parallélogramme ABCD,
- les diagonales [AC] et [BD] ont le même milieu I
- AB = DC et AD = BC
-
ABC
=
CDA
et
DAB
=
BCD
EXERCICES : n ° 2 p 137 / n ° 3 p 137

4. Propriétés réciproques
Propriétés :
1. Si les côtés opposés d’un quadrilatère sont parallèles alors ce quadrilatère est un
parallélogramme.
2. Si les côtés opposés d’un quadrilatère (non croisé) ont la même longueur alors ce quadrilatère
est un parallélogramme.
3. Si deux côtés opposés d’un quadrilatère sont parallèles et de même longueur alors ce
quadrilatère est un parallélogramme.
4. Si les diagonales d’un quadrilatère ont même milieu alors ce quadrilatère est un
parallélogramme.
5. Si les angles opposés d’un quadrilatère ont la même mesure alors ce quadrilatère est un
parallélogramme.
Exemples :
1) Énoncé : LOUP est un quadrilatère tel que LO = PU = 4 cm
et LP = OU = 6cm.
Que peut-on dire du quadrilatère LOUP ? Justifier.
Hypothèses : LO = PU et LP = OU
Or si les côtés opposés d’un quadrilatère ont la même longueur alors ce quadrilatère est un
parallélogramme.
Conclusion : LOUP est un parallélogramme.
2) Énoncé : SAXO est un quadrilatère tel que (SA) et (SO) sont
parallèles et SA = OX .
Que peut-on dire du quadrilatère SAXO ? Justifier.
Hypothèses : (SA) est parallèles à (OX) et SA = OX
Or si deux côtés opposés d’un quadrilatère sont parallèles et de même longueur alors ce quadrilatère
est un parallélogramme.
Conclusion : SAXO est un parallélogramme.
3) Énoncé : I est le milieu de [EG] et I est le milieu de [HF].
Que peut-on dire du quadrilatère EFGH ? Justifier.
Hypothèses : I est le milieu de [EG] et I est le milieu de [HF]
Or si les diagonales d’un quadrilatère ont même milieu alors ce
quadrilatère est un parallélogramme.
Conclusion : EFGH est un parallélogramme.
EXERCICES : n ° 4 p 138 / n ° 5 p 138 / n ° 6 p 138 / n ° 7 p 138
5. Tracé d'un parallélogramme
Carreaux puis équerre et règle puis compas→
EXERCICES : n ° 16 p 139 / n ° 17 p 139 / n ° 18 p 139 / n ° 19 p 139 / n ° 20 p 139

II. Parallélogrammes particuliers
1. Le rectangle
Propriété : Un rectangles est un parallélogramme donc :
• ses côtés opposés sont parallèles ;
• ses côtés opposés sont de même longueur ;
• ses diagonales se coupent en leur milieu.
De plus les diagonales d'un rectangle ont la même longueur.
Exemple :
Le parallélogramme ABCD est un rectangle,
donc AC = BD.
Remarque : OA = OB = OC = OD.
Propriété: Si un parallélogramme a deux côtés consécutifs perpendiculaires, alors c'est un rectangle.
Propriété: Si un parallélogramme possède des diagonales de même longueur, alors c'est un rectangle.
2. Le losange
Propriété: Un losange est un parallélogramme donc :
• ses côtés opposés sont parallèles ;
• ses côtés opposés sont de même longueur ;
• ses diagonales se coupent en leur milieu.
De plus les diagonales d'un losange sont perpendiculaires.
Exemple :
Le parallélogramme ABCD est un losange,
donc
AC ⊥BD.
Propriété: Si un parallélogramme a deux côtés consécutifs de même longueur, alors c'est un losange.
Propriété: Si un parallélogramme a ses diagonales perpendiculaires, alors c'est un losange.
3. Le carré
Un carré est à la fois un rectangle et un losange. Il possède donc toutes les propriétés du rectangle et
du losange.
Propriété: Si un quadrilatère est à la fois un losange et un rectangle, alors c'est un carré.
EXERCICES : n ° 8 p 138 / n ° 12 p 138 / n ° 13 p 138 / n ° 29 p 140 / n ° 30 p 140
A B
C
D
O
AB
C
D

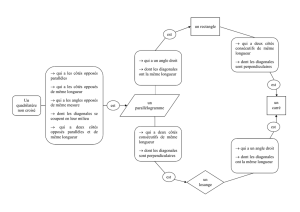
4. Schéma récapitulatif
EXERCICES : n ° 41 p 141 / n ° 42 p 141 / n ° 43 p 141 / n ° 48 p 142 / n ° 50 p 142