énoncé - Physique-Chimie LN-SPE-2 2016-2017

Lycée Naval, Spé 2.
Devoir non surveillé n◦07 (pour le 1er février 2017)
Machine asynchrone
1 Principe simplifié d’un moteur asynchrone
On dispose d’un champ magnétique qui tourne à la pulsation Ωsdans le plan xOy.
On considère une spire d’aire S, de résistance R, d’inductance propre Let de vecteur
normal ~n (Cf. figure). Cette spire, court-circuitée, tourne à la pulsation ωautour de Oz
de telle sorte que son vecteur normal reste dans le plan xOy.
B
n
x
y
O
spire
ϕ
θ
On pose θ(t) = ωt,ϕ(t)=Ωst+ Ωs0, et ωr= Ωs−ω.
On suppose de plus ω > 0.
1. Le champ magnétique est supposé homogène au sein de la spire. Calculer le flux du
champ magnétique à travers la spire.
En déduire l’expression de la f.e.m. dans la spire. On posera Φ0=B×S.
2. En considérant l’équation électrique de la spire, montrer, en passant par les gran-
deurs complexes, que l’intensité ipeut se mettre sous la forme :
i(t) = i0sin (ωrt+ Ωs0−ψ)
avec i0et ψà exprimer en fonction des données du problème.
3. Déterminer le moment ~ Γ=Γ~uzdes forces de Laplace exercé sur le cadre.
Indication : utiliser la formule ~ Γ = ~ M∧~ B.
4. En déduire la valeur moyenne de Γ, notée Γm. Montrer que ce couple peut se mettre
sous la forme :
~
Γm=Φ2
0R(Ωs−ω)
2hR2+L2(Ωs−ω)2i~uz
5. Pour toute la suite, on suppose que 0≤ω≤Ωset que LΩs/R > 1.
Montrer que le dispositif est moteur et que le couple moteur Γmen fonction de ω
a l’allure ci-contre, toutes les autres grandeurs étant fixées.
On posera Γ0= Φ2
0/(2L).
Pour l’étude de la fonction, on pourra remarquer que :
Γm=Γ0
R
L(Ωs−ω)+L(Ωs−ω) R
6. La machine est soumise à un couple résistif ~ Γ = −Γr~uz, supposé constant.
(a) Montrer que si Γrest inférieur à une certaine valeur limite, il existe en général
deux points de fonctionnement.
(b) Étudier la stabilité de ces deux points de fonctionnement.
2 Étude énergétique d’un moteur asynchrone réel
Soit un moteur asynchrone diphasé dont la plaque signalétique indique, selon le mar-
quage : Ueff = 230 V, Ieff = 18,90 A, Ωsn = 50 Hz, Pn= 5,5 kW,cos (ϕn)=0,83 et
qui comporte :
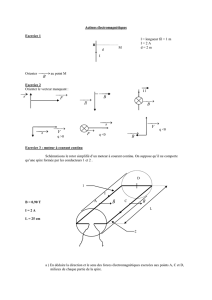
— un stator cylindrique creux d’axe Oz fixé à la carcasse, portant deux phases (B1)et
(B2)d’axes Ox1et Ox2perpendiculaires et fixes, connectées à un réseau électrique
diphasé leur délivrant des courants :
i1(t) = ˆ Iscos (Ωst) et i2(t) = ˆ Issin (Ωst),
et créant un champ magnétique d’axe Ox glissant à vitesse Ωs.
— un rotor cylindrique de même axe, rayon Rs, longueur Ls, tournant à la vitesse ω
par rapport à la carcasse ;
— deux bobines (b1) et (b2) rotoriques d’axes perpendiculaires, chacune de Nrspires,
résistance Rr, auto-inductance Lr, chacune en court-circuit, chacune parcourue par
le courant irj (t)où j∈ {1,2}induit par les effets des phases du stator ;
— un entrefer lisse de largeur econstante.
1

xr
Ox2
Ox1
ωrt
bobine b 2
Ωst
x1
xr
Ωstω +θtο −( )
x
O
stator
1
bobine B
2
bobine B
X
x
Oz
axe solidaire
du rotor
axe du champ
rotorique
axe du champ
statorique
entrefer
bobine b 1
axe fixe
M
γ(t) ο
θ =ω +θt
Les courants induits irj (t)étant sinusoïdaux, l’axe OX des pôles du rotor tourne à la
vitesse angulaire ωrpar rapport au rotor et à vitesse Ω0
r=ω+ωrpar rapport à la
carcasse du stator.
La figure précédente repère les axes, où l’on a noté Oxrune direction solidaire du rotor
et Ox1l’axe fixe de référence.
1. On repère un point Mde l’entrefer par sa position angulaire γpar rapport à
l’axe fixe. Sachant que les excitations statorique et rotorique sont spatialement
sinusoïdales au sein de l’entrefer et compte-tenu des axes des champs, montrer que
ces excitations, dirigées radialement, peuvent se mettre sous la forme :
Hs(γ, t) = ˆ Hscos (γ−Ωst) et Hr(γ, t) = ˆ Hrcos (γ−Ω0
rt−θ0),
avec ˆ Hset ˆ Hrles amplitudes des excitations statorique et rotorique et que l’on ne
cherchera pas à expliciter.
2. La perméabilité relative des parties ferromagnétiques étant supposées infinies, mon-
trer que l’énergie magnétique du dispositif stockée dans l’entrefer prend la forme :
Em=α+ˆ Ecos ([Ωs−Ω0
r]t−θ0),
avec α=µ0πLsRse׈
H2
s+ˆ
H2
r
2et ˆ
E=πRseLsµ0ˆ Hsˆ Hr.
3. En remarquant que Ωst−Ω0
rt−θ0= Ωst−ωrt−θ(t), déterminer le couple moteur
C(t).
4. Montrer que sa moyenne est non nulle pour Ωs=ω+ωr(condition que l’on
supposera vérifiée pour la suite) et que le couple moyen a pour expression :
C=−ˆ Esin (θ0)
5. Exprimer les mutuelles d’inductances M1r(t)et M2r(t)de la bobine (b1) du rotor
avec chacune des bobines du stator, à l’aide de ω,θ0et tet de leur maximum ˆ M.
Déterminer le flux mutuel Φmut1(t)à travers la bobine (b1) et montrer que la fem
er1(t)d’inductance mutuelle pour cette bobine a pour expression :
er1(t) = ˆ Φωrsin ([Ωs−ω]t−θ0),
avec ˆ Φ = ˆ Mˆ Is.
En déduire l’expression de l’amplitude complexe Er1.
6. Réaliser un schéma électrique associé à la bobine b1de l’induit. En déduire l’ex-
pression de l’amplitude complexe Ir1en fonction de Rr,Lr,ωr,θ0et ˆ Φ(attention
à l’expression de la pulsation d’excitation).
Montrer alors que le courant instantané ir1(t)a pour expression :
ir1(t) = ˆ
Φωr
pR2
r+L2 rω2 r
sin (ωrt−θ0−Ψ) avec tan (Ψ) = Lrωr
Rr
7. On admet être en régime alternatif où ce courant s’écrit :
ir1(t) = ˆ Ircos ([Ωs−ω]t)
En identifiant à l’expression précédemment obtenue, exprimer sin (θ0)et montrer
que le couple moyen prend la forme :
C=ˆ ERr
pR2
r+L2 rω2 r
8. Sachant que ˆ Eest proportionnel à ˆ Hrl’amplitude de l’excitation rotorique, montrer
que le couple est finalement proportionnel à : (Ωs−ω)
R2
r+L2 r(Ωs−ω)2.
On retrouve finalement bien une expression compatible avec celle du modèle sim-
plifié étudié dans la première partie.
2