perturbations des signaux - sur le site de Claude Lahache

1 . Généralités
On nomme perturbation un signal électrique parasite qui vient se superposer à un signal utile.
Les perturbations sont d’autant plus gênantes qu’on travaille avec des signaux utiles de faible niveau .
Quelques exemples :
• Décalage (ou offset) : Tension continue pouvant résulter de la dérive de composants
• Signal périodique (50Hz), provenant du couplage électromagnétique entre le circuit utilisé et des
conducteurs du réseau d’alimentation (cas fréquent en milieu industriel). Le même phénomène est à
l’origine du ronflement des amplificateurs audio bas de gamme (rayonnement du transformateur
d’alimentation)
• Signal aléatoire : Ce peut être une perturbation liée à l’environnement (détection parasite d’ondes
hertziennes, telle que l’influence d’un téléphone portable sur un appareillage médical). Ce peut être
également une perturbation liée à la nature même du circuit utilisé, ce qu’on nomme bruit de fond.
En résumé, les perturbations des signaux électriques peuvent être classées selon 3 origines :
- Origine « technique » : Mauvaise conception du circuit, absence de blindages, mauvais contacts, pas de
découplage des alimentations continues…
- Origine environnementale : Actions des grandeurs d’influence telles que la température ou l’humidité
(dilatations, variations de résistivité, dérive du β des transistors, vieillissements, défauts d’isolement…)
- Origine « fondamentale » : La structure microscopique de la matière constituant les composants des
circuits entraîne l’apparition de signaux aléatoires qu’on nomme le bruit de fond .
2 . Le bruit de fond.
Ce qu’on appelle habituellement « bruit de fond » correspond à un signal aléatoire b(t) qui est superposé à
un signal utile s(t).
2.1 Quelques propriétés statistiques
S’agissant d’un signal aléatoire, une tension de bruit b(t) a la même probabilité de prendre la valeur
+ u et la valeur – u au cours du temps ; la valeur moyenne
B
du bruit de fond est nulle.
Par contre, la valeur efficace du bruit de fond (B) se calcule à partir de b
2
, constamment positif ; en consé-
quence, la valeur efficace B
EFF
du bruit de fond n’est jamais nulle !
Puissance de bruit : Un bruit de valeur efficace B
EFF
, appliqué à un étage de résistance d’entrée R,
correspond à une puissance
R
B
P
2
Eff
=, soit à un niveau )log(10
mW1 P
, en dBm.

Distribution en amplitude du bruit :
Autour de sa valeur moyenne , une tension de bruit se répartit selon une loi de probabilité Gaussienne ;
la valeur moyenne du bruit étant nulle, il s’agit d’une répartition centrée réduite.
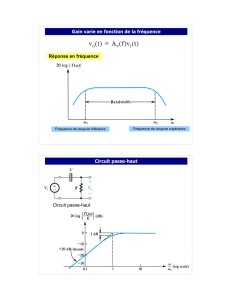
On rappelle ci-dessous quelques propriétés d’une telle fonction en « cloche » d’une variable aléatoire x. (Pour
de plus amples informations sur ce sujet, on consultera un ouvrage de mathématiques)
Nous avons
2
x
2
e
2
1
)x(f
−
π
=
pour ce genre de répartition, la probabilité
que x soit compris entre + x
1
et – x
1
correspond à l’aire sous la courbe, limitée
à droite et à gauche par + x
1
et – x
1
.
( On pourra vérifier que
+∞
∞−
=1dx).x(f )
Considérons ainsi un bruit gaussien b(t),de valeur efficace B
EFF
.
On peut voir sur la courbe ci-dessus que le bruit est de valeur nulle pendant 40% du temps !
Il est possible de montrer que nous aurons environ : 68% de chance de trouver b(t) entre ± B
EFF
, 95% de
chance de trouver b(t) entre ± 2B
EFF
, 99% de chance de trouver b(t) entre ± 3B
EFF
.
On constate que la tension instantanée de bruit b(t) ne dépasse quasiment jamais la valeur ± 3B
EFF
; il est
possible de mesurer convenablement une tension efficace de bruit, en admettant que B
EFF
≈ B
CC
/6
BCC
≈
≈≈
≈
6BEFF
BEFF

2.2 Spectres des bruits.
Ce sont des signaux aléatoires ; il faut donc prévoir des spectres de bande et non de raies.
Selon la forme du spectre, on classe les bruits en 2 grandes catégories :
- Les bruits blancs, dont la répartition spectrale est indépendante de la fréquence.
- Les bruits colorés, dont la répartition spectrale dépend de la fréquence ; le bruit rose en est un exemple
classique (répartition spectrale décroissant avec la fréquence)
Voir ci-dessous des exemples illustratifs :
2.3 Bruit de fond thermique.
C’est le bruit observé dans les résistances, c’est à dire dans tous les composants !
Dans une résistance, l’agitation thermique des porteurs de charge libres (électrons) conduit à de véritables
courants désordonnés, dont la valeur moyenne est bien sur nulle.
Ces déplacements entraînent l’existence d’une fém aléatoire e
N
(t) aux bornes de cette résistance. La valeur
moyenne de e
N
(t) est nulle, mais pas sa valeur efficace E
N
.
On montre que la fém efficace de bruit thermique E
N
aux bornes d’une résistance R s’exprime par :
fkTR4E
N
∆=
avec T : température absolue, en K ; k ≈ 1,38×10
-23
Js : constante de Boltzmann et ∆f : bande de fréquences
considérée.
La fém de bruit est d’autant plus élevée que la résistance R est de forte valeur, et que la bande passante de
l’étage est grande. (E
N
est multipliée par 3 environ lorsque la valeur de R est décuplée : Il faudra veiller à
limiter les valeurs des résistances utilisées si on désire un étage à faible bruit !)
D’un point de vue spectral, le bruit thermique est un bruit blanc.
Exemples : Quelques fém efficaces de bruit thermique, à la température de 300K .
R = 10k
Ω R = 100k Ω R = 1M Ω R = 10M Ω
∆ f = 20kHz 1,8µV 5,8µV 18µV 58µV
∆ f = 300kHz 7,0µV 22,3µV 70µV 223µV
∆ f = 5MHz 28,8µV 91µV 288µV 910µV
Bruit blanc dans la bande 0 – 100kHz Bruit blanc dans la bande 0 – 8MHz, rose au delà

2.4 Autres bruits de fond.
Dans un semi-conducteur, et notamment les jonctions PN, il y a constamment création et disparition
de paires électron-trou. Il s’en suit une tension de bruit b(t).
b(t) fluctue au gré de la production et de la disparition de paires électron-trou : on l’appelle le bruit de
génération-recombinaison . Ce bruit existe même en l’absence de courant ( i(t)=0 ).
Le courant dans une jonction est lié à la circulation des porteurs (électrons et trous). Le courant
électrique, qui paraît continu à l’échelle macroscopique, est, au niveau microscopique, constitué par un grand
nombre d’impulsions de courant élémentaires (chaque impulsion correspondant au déplacement d’un
électron).
En présence d’un courant « constant » I ≠ 0 , I fluctue autour de sa valeur moyenne parce que le courant est
constitué par une superposition de courants impulsionnels: c’est le bruit de grenaille.
Ce bruit augmente avec le courant I ; il est blanc jusqu’à des fréquences supérieures à 1GHz.
La valeur efficace de ce bruit en courant est donné par la formule de Schottky : fqII
eff
∆= 2
avec q = 1,6×10
-19
C ; I : courant continu dans la jonction ; ∆.f : bande de fréquences utiles .
Par exemple, pour une diode traversée par un courant de I = 1mA et une bande de
∆ .f = 1MHz, la valeur
efficace du bruit en courant vaut : I
eff
= 18 nA.
Aux basses fréquences existe un autre type de bruit nommé le bruit en 1/f . (bruit de Flicker)
Ce bruit est lié à la présence de défauts ou d’impuretés au sein d’un semi-conducteur.
Le bruit en 1/f décroît avec la fréquence et apparaît non seulement dans les semi-conducteurs, mais aussi dans
les résistances au carbone. La bande de fréquence où il est supérieur au bruit thermique tend à se rétrécir au
fur et à mesure des progrès technologiques et ne dépasse pas quelques dizaines de Hz pour les meilleures
technologies actuelles.
Conséquence : Le bruit de fond global dans un composant correspond à la superposition de ces différents
types de bruits.
A titre indicatif, on donne l’allure de la densité spectrale de bruit dans quelques composants :
(La densité spectrale de bruit, pour une fréquence f
o
, est simplement la tension efficace de bruit ramenée à une
bande de fréquence de 1Hz autour de f
o
.)
On peut remarquer que ces bruits totaux sont roses aux basses fréquences, puis blancs au delà.
Ω
ΩΩ
Ω

3 . Bruit dans une chaine de traitement de signal.
3.1 Modélisation d’un dipôle bruyant
Un dipôle bruyant sera représenté par un dipôle sans bruit associé à une source de bruit selon un modèle qui
peut être de Thévenin ou de Norton.
Exemples :
3.2 Modélisation d’un quadripôle bruyant.
Le bruit en sortie d’un quadripôle est produit par tous les composants internes au quadripôle.
On peut caractériser le bruit total en sortie en introduisant deux sources de bruit : Une source de tension U
(type bruit thermique) et une source de courant I (type bruit de grenaille), placées à l’entrée du quadripôle.
C’est le modèle le plus fréquemment utilisé.
Dans le cas des amplificateurs, les constructeurs spécifient les tensions et courant efficaces de bruit ramenées
à l’entrée, exprimées respectivement en nV/√Hz ou en pA/√Hz.
Voir ci-dessous un exemple de données constructeur relatives à un amplificateur opérationnel courant.
R
BEFF
IEFF
Résistance bruyante
Diode bruyante
U
R
I
Quadripôle
non bruyant u
S