Télécharger

Notion de gravitation
1
NOM Prénom : ………………………………………………………………………………………………………….
Classe : …………..
Date : ………………………………
Exercice I : Quelques questions de cours
1. Complète le texte suivant
a. Le système solaire est composé du Soleil et de huit planètes qui décrivent une trajectoire circulaire/elliptique autour du
Soleil.
b. Le mouvement des planètes autour du Soleil est dû à la gravitation exercée par le Soleil et la force centrifuge.
c. Un objet qui possède une certaine masse exerce une action attractive à distance sur un autre objet.
d. La gravitation est proportionnelle à la masse et inversement proportionnel à la distance qui sépare 2 corps.
2. Une pomme chute d’un pommier. Pourquoi la pomme tombe-t-elle ?
Car elle est attirée par la Terre.
Exercice II : Les bolas !
Les bolas sont des instruments de jonglerie. Ils sont composés de chaînes au bout desquelles
sont attachées des boules enflammées. Les figures sont exécutées en faisant tournoyer les
bolas.
1. Quand un jongleur fait tourner ses bolas s’agit-il d’une action de contact ou à
distance ?
Les bolas et le jongleur sont reliés par les chaines donc c’est une action de contact.
2. Quel mouvement décrivent les bolas quand on les fait tournoyer ?
Elles décrivent un mouvement circulaire/ de révolution.
3. Si on compare ce jeu au système solaire, qui joue le rôle d’une planète et qui joue le rôle du Soleil ?
La main du jongleur joue le rôle du Soleil.
Les bolas jouent le rôle des planètes.
4. Quelle différence y a-t-il entre cette analogie et le système solaire ?
Dans le cas des bolas, il s’agit d’une action de contact alors que dans le système solaire, on parle d’action à distance.
Exercice III : Les exoplanètes
Télescopes pointés vers le ciel, l’œil rivé sur l’écran de contrôle, les astronomes se sont lancés dans une nouvelle chasse : la
chasse aux exoplanètes. Une exoplanète (ou planète extrasolaire) est un corps gravitant autour d’une étoile autre que notre
Soleil. La première exoplanète fut détectée en 1995 dans la constellation de Pégase. A l’observatoire de haute Provence, deux
astronomes suisses ont détecté une petite planète nommé 51Pegb gravitant autour de l’étoile 51 Pegasi à 40 années-lumière de
notre Terre. Depuis, plus de 200 planètes ont été détectées et leur nombre augmente avec les progrès techniques. La majorité
de ces planètes sont des géantes gazeuses. L’annonce en janvier 2006 de la découverte d’une planète tellurique (possédant un
sol) située à 25 000 années lumières de notre Terre et dont les caractéristiques se rapprochent de celles de notre planète
relance le débat millénaire : parmi les cent milliards de galaxies, existe-t-il une étoile autour de laquelle gravite une planète sur
laquelle s’est développée une autre forme de vie ? Existe-t-il d’autres systèmes solaires ? «Sommes-nous seuls dans l’Univers ?»
1. Qu’est-ce qu’une exoplanète ? Cite 1 exemple.
Une exoplanète est une planète évoluant dans un système autre que notre système solaire. Exemple : 51 Pegb.
2. Pourquoi s’intéresse-t-on plus particulièrement aux exoplanètes telluriques ?
Car elles possèdent un sol et donc peuvent potentiellement accueillir la vie !
Exercice IV : Les lois de Kepler
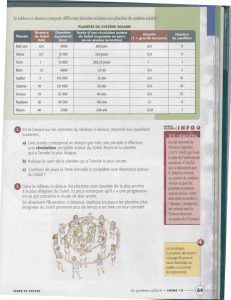
Au début du XVII° siècle, l’astronome allemand Johannes Kepler établit des lois qui gouvernent le mouvement des planètes
autour du Soleil. En particulier la 3° loi de Kepler relie les périodes de révolution T des planètes autour du Soleil aux rayons R de
leurs orbites :
La période est le temps nécessaire à la planète pour faire un tour autour du Soleil.
Par exemple, pour la Terre, T = 365,25 j et R = 150x106 km ; pour Mars, T = 687 j et R = 228x106 km.
1. Calculer le rapport  
 pour la Terre. Attention aux unités et aux parenthèses de la calculatrice !
2. Calculer le rapport  
 pour Mars. Comparer au résultat de la question précédente !
Les résultats sont quasiment identiques.
3. La période orbitale de Venus étant de 224.7j, déterminez le rayon de son orbite. Utiliser la constante des questions 1 et2.
On utilise la formule suivante :  
Ce qui signifie que le rayon de l’orbite vaut :    

Notion de gravitation
1
NOM Prénom : ………………………………………………………………………………………………………….
Classe : …………..
Date : ………………………………
Exercice I : Quelques questions de cours
1. Complète le texte suivant
a. Le système solaire est composé du Soleil et de huit planètes qui décrivent une trajectoire circulaire/elliptique autour du
Soleil.
b. Le mouvement des planètes autour du Soleil est dû à la gravitation exercée par le Soleil et la force centrifuge.
c. Un objet qui possède une certaine masse exerce une action attractive à distance sur un autre objet.
d. La gravitation est proportionnelle à la masse et inversement proportionnel à la distance qui sépare 2 corps.
2. Une pomme chute d’un pommier. Pourquoi la pomme tombe-t-elle ?
Car elle est attirée par la Terre.
Exercice II : Les bolas !
Les bolas sont des instruments de jonglerie. Ils sont composés de chaînes au bout desquelles
sont attachées des boules enflammées. Les figures sont exécutées en faisant tournoyer les
bolas.
1. Quand un jongleur fait tourner ses bolas s’agit-il d’une action de contact ou à
distance ?
Les bolas et le jongleur sont reliés par les chaines donc c’est une action de contact.
2. Quel mouvement décrivent les bolas quand on les fait tournoyer ?
Elles décrivent un mouvement circulaire/ de révolution.
3. Si on compare ce jeu au système solaire, qui joue le rôle d’une planète et qui joue le rôle du Soleil ?
La main du jongleur joue le rôle du Soleil.
Les bolas jouent le rôle des planètes.
4. Quelle différence y a-t-il entre cette analogie et le système solaire ?
Dans le cas des bolas, il s’agit d’une action de contact alors que dans le système solaire, on parle d’action à distance.
Exercice III : Les exoplanètes
Télescopes pointés vers le ciel, l’œil rivé sur l’écran de contrôle, les astronomes se sont lancés dans une nouvelle chasse : la
chasse aux exoplanètes. Une exoplanète (ou planète extrasolaire) est un corps gravitant autour d’une étoile autre que notre
Soleil. La première exoplanète fut détectée en 1995 dans la constellation de Pégase. A l’observatoire de haute Provence, deux
astronomes suisses ont détecté une petite planète nommé 51Pegb gravitant autour de l’étoile 51 Pegasi à 40 années-lumière de
notre Terre. Depuis, plus de 200 planètes ont été détectées et leur nombre augmente avec les progrès techniques. La majorité
de ces planètes sont des géantes gazeuses. L’annonce en janvier 2006 de la découverte d’une planète tellurique (possédant un
sol) située à 25 000 années lumières de notre Terre et dont les caractéristiques se rapprochent de celles de notre planète
relance le débat millénaire : parmi les cent milliards de galaxies, existe-t-il une étoile autour de laquelle gravite une planète sur
laquelle s’est développée une autre forme de vie ? Existe-t-il d’autres systèmes solaires ? «Sommes-nous seuls dans l’Univers ?»
1. Qu’est-ce qu’une exoplanète ? Cite 1 exemple.
Une exoplanète est une planète évoluant dans un système autre que notre système solaire. Exemple : 51 Pegb.
2. Pourquoi s’intéresse-t-on plus particulièrement aux exoplanètes telluriques ?
Car elles possèdent un sol et donc peuvent potentiellement accueillir la vie !
Exercice IV : Les lois de Kepler
Au début du XVII° siècle, l’astronome allemand Johannes Kepler établit des lois qui gouvernent le mouvement des planètes
autour du Soleil. En particulier la 3° loi de Kepler relie les périodes de révolution T des planètes autour du Soleil aux rayons R de
leurs orbites :
La période est le temps nécessaire à la planète pour faire un tour autour du Soleil.
Par exemple, pour la Terre, T = 365,25 j et R = 150x106 km ; pour Mars, T = 687 j et R = 228x106 km.
1. Calculer le rapport  
 pour la Terre. Attention aux unités et aux parenthèses de la calculatrice !
2. Calculer le rapport  
 pour Mars. Comparer au résultat de la question précédente !
Les résultats sont quasiment identiques.
3. La période orbitale de Venus étant de 88j, déterminez le rayon de son orbite. Utiliser la constante des questions 1 et2.
On utilise la formule suivante :  
Ce qui signifie que le rayon de l’orbite vaut :    