LEÇON 14 THÉORÈME DES ACCROISSEMENTS FINIS

LEÇON 14
THÉORÈME DES ACCROISSEMENTS FINIS - APPLICATIONS
Le plan affine euclidien Pest rapporté au repère orthonormé (O,~ı, ~ ).
Soit f: [a, b]−→ R, continue sur [a, b], dérivable sur ]a, b[ et
vérifiant f(a) = f(b). Alors il existe un réel c∈]a, b[ tel que
f0(c) = 0.
Lemme 0.1 (Théorème de Rolle).
I. Théorème des accroissements finis
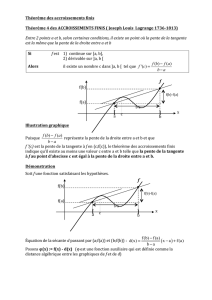
Soit f: [a, b]−→ R, continue sur
[a, b], dérivable sur ]a, b[. Alors il
existe un réel c∈]a, b[ tel que :
f(b)−f(a) = f0(c)(b−a)
Théorème 1.1.
Interprétation géométrique : Il existe
au moins un point de ]a, b[ où la tan-
gente à la courbe Cfest parallèle à la
droite (AB), avec A=a, f (a)et
B=b, f(b).
Oab
Cf
f(a)A
f(b)B
14. Théorème des accroissements finis - Applications Fabien PUCCI

2Théorème des accroissements finis - Applications
Remarques: Le théorème des accroissement finis se généralise pour une
fonction de classe Cnsous la forme du théorème de Taylor-Lagrange :
∃c∈]a, b[,
f(b)−f(a) = (b−a)f0(a) + ...+(b−a)n
n!f(n)(a) + (b−a)n+1 (n+ 1)! f(n+1)(c).
II. Inégalité des accroissements finis
II.1 Fonctions à valeurs dans R
Soient fet gdeux fonctions à valeurs dans R, définies et continues
sur [a, b], dérivables sur ]a, b[. Si, pour tout t∈]a, b[, f0(t)6g0(t)
alors, pour tout couple (x, y)∈[a, b]2tel que x < y :
f(y)−f(x)6g(y)−g(x).
Théorème 2.1.
Applications : ∀x∈−1
2,+∞,ln(1 + x)−x6x2.
Soit f: [a, b]7−→ Rcontinue sur
[a, b] et dérivable sur ]a, b[.
S’il existe deux réels m, M tels
que :
∀x∈]a, b[, m 6f0(x)6M.
Alors on a :
m6f(b)−f(a)
b−a6M.
Corollaire 2.2.
Oab
Cf
f(a)
f(b)
(m)
(M)
(D0)
(D)
(∆0)
(∆)
*
Interprétation géométrique : Notons Cfla courbe représentative de fsur
[a, b].
Soit x∈[a, b].
x>a⇒m(x−a) + f(a)6f(x)6M(x−a) + f(a),
x6b⇒M(x−b) + f(b)6f(x)6m(x−b) + f(b).
On note (D) : y=m(x−a) + f(a), (D0) : y=m(x−b) + f(b),
(∆) : y=M(x−a) + f(a) et (∆0) : y=M(x−b) + f(b).
Dans ce cas, Cfest comprise dans le parallélogramme délimité par ces
quatre droites.
Soit f: [a, b]7−→ Rcontinue sur [a, b] et dérivable sur ]a, b[. S’il
existe un réel k > 0 tel que : ∀x∈]a, b[,|f0(x)|6kalors on a :
|f(b)−f(a)|6k|b−a|.(14.1)
Corollaire 2.3.
Fabien PUCCI 14. Théorème des accroissements finis - Applications

III. Applications 3
Les fonctions vérifiant l’inégalité 14.1 sont dites k-lipschitzienne. Sans
être nécessairement dérivables, elles sont continues.
II.2 Fonctions à valeurs dans Rn
Lorsque les applications sont à valeurs dans un R-evn, le théorème
des accroissements finis 1.1 n’est plus vrai comme le montre l’applica-
tion f: [0,2π]−→ C
t7−→ eit
qui vérifie f(0) = f(2π) sans que f0(t) = ieit
ne soit jamais nul sur [0,2π].
Par contre, les inégalités du type de 14.1 subsistent :
Soit F: [a, b]7−→ Eune application à valeurs dans un R-evn
continue sur [a, b], dérivable sur ]a, b[. S’il existe k > 0, tel que
kF0(t)k6kpour tout t∈]a, b[ alors :
kF(b)−F(a)k6k|b−a|.
Théorème 2.4.
Soit F: [a, b]7−→ Eune application continue, dérivable sur ]a, b[
telle que lim
x→a
x>a
f0(t) = `. Alors Fest dérivable en aet F0(a) = `.
Corollaire 2.5.
III. Applications
III.1 Etude de fonctions
Soit f: [a, b]−→ Rune fonction continue sur [a, b] et dérivable
sur ]a, b[. On suppose que f0(x)>0 sur ]a, b[. Alors, pour tout
x∈[a, b], on a : f(x)>f(a).
Théorème 3.1.
Soit f: [a, b]−→ Rune fonction continue sur [a, b] et dérivable
sur ]a, b[. Si f0>0 sur ]a, b[ si et seulement si fest croissante sur
[a, b].
Corollaire 3.2.
Soit Iun intervalle de R(non vide et non réduit à un point).
Soit fune application dérivable sur I. Alors f0vérifie la propriété
des valeurs intermédiaires :
∀(a, b)∈I2,f0prend toute valeur intermédiaire comprise entre
f0(a) et f0(b).
Théorème 3.3 (Darboux).
Remarque: f0n’est pas, a priori, supposée continue et c’est très loin
d’être le cas !
14. Théorème des accroissements finis - Applications Fabien PUCCI

4Théorème des accroissements finis - Applications
III.2 Encadrements
•Soit f:R−→ Rdéfinie par f(x) = cos(x), continue et dérivable sur
R. Pour tout réel x,f0(x) = −sin(x)⇒ |f0(x)|61. Donc, par le
corollaire 2.3, on a :
∀x, y ∈R,cos(x)−cos(y)6|x−y|
De même, pour tous x, y ∈R,
sin(x)−sin(y)6|x−y|.
•On cherche à encadrer √105. On considère f(x) = √xsur [100,105].
Alors
f0(x) = 1
2√x⇒1 22 61
2√105 6f0(x)61 2√100 =1
20.
D’après le théorème 2.2, on obtient donc
1
22(105 −100) 6√105 −√100 61 20(105 −100)
5
22 + 10 6√105 65 20 + 10
10,227 6√105 610,25.
III.3 Nature de certaines suites
•
n
X
k=1
1
k∼
n→+∞ln n.
Soient un=
n
X
k=1
1
ket vn= ln(n) pour tout n∈N∗. Posons f(x) = ln(x),
de sorte que f0(x) = 1
x. Alors, si x∈[k, k + 1],
1
k+ 1 61 x61 k
Co 2.2
⇒1
k+ 1 6ln(k+ 1) −ln(k)61 k.
En sommant, on trouve alors
n
X
k=1
1
k+ 1 6ln(n+ 1) 6
n
X
k=1
1
k
un−1 + 1
n+ 1 6ln(n+ 1) 6un
ln(n+ 1) 6un6ln(n+ 1) + 1 −1
n+ 1.
III.4 Point fixe
Soient f: [a, b]−→ Rcontinue sur [a, b] et dérivable sur ]a, b[, et
k∈]0,1[. On suppose que f[a, b]) ⊂[a, b]. Si l’on a |f0(x)|6k
pour tout x∈]a, b[, alors l’équation f(x) = xadmet une unique
solution x∗dans [a, b].
Théorème 3.4.
x∗est appelé point fixe de f.
Si fest une fonction vérifiant les hypothèses du théorème 3.4, alors
la suite définie par u0∈[a, b] et pour tout n∈N,un+1 =f(un)
converge vers x∗et l’on a la majoration de l’erreur pour tout n:
|un−x∗|6kn|b−a|.
Corollaire 3.5.
Applications : Déterminer une valeur approchée au millième, puis à
10−4près, de la solution de l’équation x3+ 4x−1 = 0.
Fabien PUCCI 14. Théorème des accroissements finis - Applications

VI. Exercices 5
IV. Idées de développement
•Contrôle de l’erreur dans les méthodes approchées de calcul d’inté-
grales. (Simpson Go p 28)
•Théorème de Darboux (dur !)
V. Références
– Alain Pommellet, Agrégation de mathématiques - Cours d’analyse,
Ellipses
– Xavier Gourdon, Les maths en tête, Mathématiques pour M∗- ANA-
LYSE, Ellipses
VI. Exercices
Exercice 6.1: Montrer que ∀x∈−1
2,+∞, ln(1 + x)−x6x2.
Correction: Pour x>−1
2, posons f(x) = x−ln(1 + x). fvérifie les hypothèses
du théorème 2.3 avec f0(x) = x
1 + x62x. En posant g(x) = x2, sur l’intervalle [0, x] :
ln(1 + x)−x6x2.
Remarque: sur [0,+∞[, le même raisonnement conduit à 0 6f0(t)6tpuis à l’in-
égalité :
06ln(1 + x)−x6x2
2.
Exercice 6.2: Montrer que pour tous x, y ∈R\π
2+πZ,
tan(x)−tan(y)>|x−y|.
Correction: On a :
x2>0⇒0<1
x2+ 1 61.
Or arctan0(x) = 1/(x2+ 1), donc pour tous X, Y ∈R, on a
|arctan X−arctan Y|6|X−Y|. En prenant xet yde sorte que X= tan(x) et
Y= tan(y), on arrive au résultat demandé : |x−y|6|tan x−tan y|.
Exercice 6.3: Dans l’application du théorème des accroissements finis à la fonction
f(x) = αx2+βx +γ
sur l’intervalle [a, b] préciser le nombre « c» de ]a, b[.
Donner une interprétation géométrique.
Correction: La fonction fest continue et dérivable sur Rdonc en particulier sur
[a, b]. Le théorème des accroissement finis assure l’existence d’un nombre c∈]a, b[ tel
que f(b)−f(a) = f0(c)(b−a).
Mais pour la fonction particulière de cet exercice nous pouvons expliciter ce c. En
effet f(b)−f(a) = f0(c)(b−a) implique α(b2−a2) + β(b−a) = (2αc +β)(b−a). Donc
c=a+b
2.
Géométriquement, le graphe Pde fest une parabole. Si l’on prend deux points
A= (a, f(a)) et B= (b, f(b)) appartenant à cette parabole, alors la droite (AB) est
parallèle à la tangente en Pqui passe en M= (a+b
2, f(a+b 2)). L’abscisse de Métant le
milieu des abscisses de Aet B.
14. Théorème des accroissements finis - Applications Fabien PUCCI