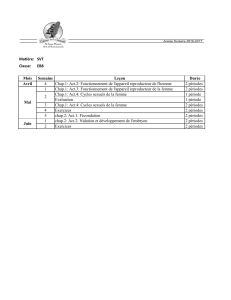
Chapitre n°15 : Trigonométrie Activité d`approche n°1

1/11 – Chap.n°15:Trigonométrie
Chapitre n°15 : Trigonométrie
Objectifs :
Enroulement de la droite numérique sur le cercle trigonométrique et définition du sinus et du
cosinus d’un nombre réel. Lien avec les valeurs des sinus et cosinus des angles de 0,30,45,60 et
90°.
Activité d'approche n°1
Partie I : Préambule historique et physique.
Les accélérateurs de particules sont des instruments permettant d'amener des particules
chargées (électrons, protons, …) à des vitesses élevées. Pour cela, ils utilisent des champs
électriques et magnétiques. Ils sont utilisés pour le traitement des cancers, et pour la
recherche de la structure de notre univers.
L'accélération A à laquelle est soumis une particule dans un champs électrique est donnée par la
formule :
A=qE
m
(1) où :
q est la charge de la particule, E le champ électrique et m la masse de la particule.
La vitesse V est alors, en fonction du temps :
V=qEt
m
(2)
La position P de la particule, en fonction du temps :
P=qEt2
2m=A t 2 2
(3)
La particule subissant constamment une accélération, on voit que plus la particule est soumise
longtemps au champ électrique, plus elle peut atteindre des vitesse très élevées. Autrement dit,
plus le trajet parcouru par la particule est long, et plus la vitesse en fin de parcours est
élevée.
Il faut cependant qu'il y ait du vide le long de la trajectoire (sinon la particule risque de cogner
dans d'autres particules).
1. Exprimer t en fonction de P. On appellera la relation obtenue la
relation (4) :
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
1/11

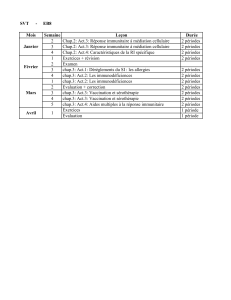
2/11 – Chap.n°15:Trigonométrie
Partie II : un accélérateur linéaire, le Stanford Linear ACcelerator.
En 1966 fut construit l'un des premier accélérateur à grande échelle : le
SLAC, en Californie, mesurait 3,2 km de long, en ligne droite.
Pour le SLAC, pour un électron
m = 9,10 × 10-31 Kilogramme,
E=30×10+6 Volt par mètre,
q= 1,60×10- 19 Coulomb
1. Calculer l'accélération A pour un
électron en utilisant la relation (1) (avec
trois chiffres significatifs) :
Calcul :....................................................................
.............................................................................
Résultat :....................................................
Les particules partent du milieu du SLAC
(en O) (les particules de charges négatives
vers le bas, celles de charge positive vers
le haut). A et B sont les extrémités de
l'accélérateur.
2. Quelle distance P a parcouru un électron
(particule négative) quand il arrive en B ?
Calcul :...................................................................
.................................................................................
Résultat :....................................................
3. En déduire le temps t qui s'est écoulé
depuis le départ en O. (on donnera le résultat avec trois chiffres significatifs et on
utilisera la relation (4))
Calcul :...................................................................................................................................................
.................................................................................................................................................................
................................................................................................................................................................
Résultat :....................................................
4. En déduire la vitesse de la particule en B. (on donnera le résultat avec trois
chiffres significatifs – utiliser une des relations de la partie I)
2/11
+
-
A
B
O
K
J
L

3/11 – Chap.n°15:Trigonométrie
Calcul :...................................................................................................................................................
.................................................................................................................................................................
................................................................................................................................................................
Résultat :....................................................
Partie III : un accélérateur circulaire.
Pour allonger la longueur de la trajectoire, et donc augmenter la vitesse de la
particule, on crée un accélérateur circulaire, de rayon 1 km, pour remplacer le
SLAC.
a. Rappeler la formule du périmètre d'un cercle : …......................................
b. Quelle distance exacte parcourt un électron quand il fait un tour complet ?
…..............................................…..........................................................................................
…...........................................................................................................................................
c. En utilisant la même technique que dans la partie 1, calculer sa vitesse
approchée au bout d'un tour.
….................................................................................................................................................
…..................................................................................................................................................
.....................................................................................................................................................
.................................................................................................................................................
....
d. Calculer la distance exacte parcourue par un électron,
puis par un proton (charge positive, donc le trajet dans le
sens inverse) lorsqu' ils seront respectivement
en K, J et L.
3/11
+
-
A
B
O
K
J
L

4/11 – Chap.n°15:Trigonométrie
…..................................................................................................................................................
.....................................................................................................................................................
.....................................................................................................................................................
.....................................................................................................................................................
.....................................................................................................................................................
....................................................................................................................................................
e. Calculer la distance exacte parcourue par un électron, puis par un proton
(charge positive) lorsqu' ils auront effectués :
- un quart de tour :
…...............................................................................................................................
- un huitième de tour :
…...........................................................................................................................
- cinq huitièmes de tour :
…................................................................…................................................................
- un tour et un sixième de tour :
….................................................................…...........................................................................
- un sixième de tour : ….......................................................................................................
- un douzième de tour : …....................................................................................................
f. Placer le plus précisément possible les positions d'un proton et d'un électron
à la fin de chacun de leur parcours de la question e.
g. Un électron est dans le SLAC, en B. On souhaite savoir où il serait placé,
dans l'accélérateur circulaire. Sachant qu'un tour complet correspond à 2π, quel
calcul peut-on faire pour placer cet électron ?
….................................................................…...........................................................................
….................................................................…...........................................................................
Le placer.
h. Un proton est placé en J, dans l'accélérateur circulaire. Quel calcul peut-on
faire pour placer ce proton dans le SLAC ?
….................................................................…...........................................................................
Le placer.
i. On se place dans l'accélérateur circulaire.
Où sera situé un proton lorsqu'il aura parcouru
3π
4
km ?
11 π
4
km ?
19 π
4
Km ?
Où sera situé un électron lorsqu'il aura parcouru
5π
4
km ?
13 π
4
km ?
21 π
4
Km ?
4/11

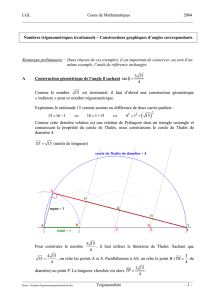
5/11 – Chap.n°15:Trigonométrie
Cours n°1
Chapitre n°15 : Trigonométrie
I) Cercle trigonométrique
Définition n°1 : cercle trigonométrie
Le cercle de centre O et de rayon ... unité, sur lequel on a choisi un sens
p........................., le sens ….......................... des aiguilles d'une montre, est appelé
cercle trigonométrique.
Définition n°2 : nombre associé à un point du cercle.
On munit le plan d'un repère orthonormé (O;I;J) , du
cercle trigonométrique c de centre O, et de la droite
d d'équation x=1.
Alors, le nombre x associé à un point M du cercle c est
la d................................. qui sépare le point I du point N
sur d quand on déroule le cercle sur la droite d et que
M arrive sur N.
Remarque : on peut faire plusieurs fois le tour du
cercle et « retomber » sur le point M. Autrement dit,
pour un même point M du cercle il existe une infinité de nombres associés : x,
x+2, x+ 4 , x + 6 ...
II) Longueur d'arc
Propriété n°1 (rappel)
La longueur d'arc est …............................................ à l'angle qui l'intercepte.
Exemple n°1
Donnez les longueurs des arcs associées du cercle trigonométrique aux angles
en degré suivant :
Degrés 0° 30° 45° 60° 90° 180°
Longueur ............... ............... ............... ............... ............... ...............
5/11
I
x
x
M
N
J
O