mecaflu_c4_td - CPGE Brizeux

Mécaflu_C4 Exercices PC
Bilans macroscopiques
1. Canalisation horizontale
Une canalisation horizontale est parcourue par un liquide décrit comme un fluide parfait incompressible de masse
volumique m. La vitesse est
⃗
v1=v1⃗ ux
et la pression p0 au
niveau de la section S1. L’écoulement est stationnaire et
unidimensionnel. On suppose connues les valeurs de m, p0, v1, S1 et
S2 (aires des sections S1 et S2).
L’atmosphère extérieure est à la pression p0. On néglige la
pesanteur.
1) Exprimer le débit en masse Dm de l’écoulement en fonction de
m, v1 et S1.
2) Exprimer la vitesse
⃗v2
et la pression p2 au niveau de S2 en fonction des données.
3) Calculer la force totale
⃗
F
subie par la portion de canalisation située entre S1 et S2 de la part du fluide et de l’air
extérieur.
2. Canalisation coudée
Une canalisation de section uniforme d’aire S fait un coude
d’angle θ; elle contient un fluide incompressible de masse
volumique μ dont l’écoulement, loin du coude, est parfait,
stationnaire et unidimensionnel.
Dans la section d’entrée, la vitesse est uniforme (elle se note
⃗
v
)
et la pression également (elle se note p). On néglige les effets de
la pesanteur.
Déterminer la direction et la norme de la force exercée par le
fluide sur la canalisation, en fonction de μ, θ, p, S et le débit
volumique D de l’écoulement.
Application numérique: Le liquide est de l’eau qui coule avec un débit volumique de 10,0 litres par seconde dans un
tuyau de 4,0 cm2 de section droite présentant un coude de 60°(p = 2bar).
3. Gouttes de pluie
Il pleut sur une fenêtre de surface SF = 2,0 m2. On considère que les gouttes ont des trajectoires
rectilignes parallèles entre elles qui font un angle a de 30° par rapport à la verticale. Le débit D
est de 800 gouttes par m3, une goutte ayant toujours une vitesse de module v = 2 m.s-1 et une
masse m = 0,1 g. On suppose que les gouttes rebondissent sur la vitre de façon à considérer les
chocs comme élastiques.
Déterminer la force de pression subie par la vitre.
4. Tuyau d'arrosage
Un tuyau souple, de section S se termine par un embout dont la section terminale s est très petite devant S. La pression
dans le tuyau est P1 et le jet sort dans l'atmosphère à la pression P0. L'embout fait un angle droit avec la partie
antérieure du tuyau. La vitesse du jet sera supposée très grande devant la vitesse du fluide dans le tuyau.
L'eau étant assimilée à un fluide parfait, calculer le débit massique Dm. et Fy,
composante parallèle au jet de la force
⃗
F
exercée par la personne qui tient la
lance.
L’écoulement est supposé parfait, unidimensionnel et stationnaire et l’on
néglige les forces de pesanteur.
Données : P1 = 10 bars; P0 = 1 bar; s = 1 cm2.
1

5. Jet sur une plaque circulaire
Une plaque circulaire de rayon r se déplace avec la vitesse constante
⃗
v0=v0⃗ ux
par rapport au sol. Elle reçoit un jet
d’eau de masse volumique
ρ
et de vitesse
⃗
v ' =v ' ⃗ ux
par rapport au sol et de section d’aire S connue.
On néglige l’effet de la pesanteur. Après le choc sur la plaque, le jet se partage de manière symétrique par rapport à
l’axe de révolution de la plaque, l’aire totale du jet ainsi crée étant S ’.
1) On note R le référentiel lié au sol et R’ celui lié à la plaque. On choisit des sections des jets S et S’ loin de la plaque.
a) Exprimer dans le référentiel R’ la vitesse d’une particule de fluide au niveau de S.
b) Même question pour une particule au niveau de S’.
2) Quelle est la résultante des forces subie par la plaque de la part de l’air et du jet ?
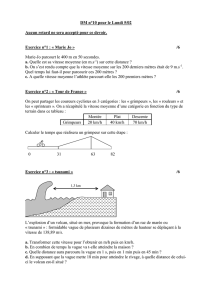
6. Étude d'un mascaret
La marée haute engendre à l'embouchure de certains fleuves une vague de hauteur h qui remonte à la vitesse
vv
supposée constante. On note H la hauteur du fleuve en l'absence de vague et H' = H + h la profondeur en présence de la
vague. Le fleuve a une largeur L . Il s'écoule à la vitesse
v0
en amont de la vague. La vague est modélisée par une
marche rectangulaire. On suppose l'eau incompressible. On note
ρ
la masse volumique de l'eau.
On se place dans le référentiel lié à la vague. Dans ce référentiel l'eau du fleuve se déplace à la vitesse V en amont de la
vague et V' en aval (shéma ci-dessous).
a) Justifier le choix du référentiel, déterminer la relation entre H, H', V et V' traduisant la conservation de la masse
b) La pression atmosphérique est égale à
P0
. On admet que la pression de l'eau varie comme en hydrostatique en
amont et en aval de la vague. En faisant un bilan de quantité de mouvement en déduire une nouvelle relation entre les
différentes grandeurs du problème.
c) En déduire une expression de V en fonction g, h et H. Que devient cette expression si h << H ?
d) A quelle condition dur la vitesse
v0
, le mascaret peut-il remonter le fleuve ?
e) On néglige cette vitesse
v0
. La première vague fait passer la profondeur de H à H' . Elle est suivie d'une seconde
vague qui fait passer la profondeur de H' à H''. Que se passe-t-il ?
f) Grâce à un bilan énergétique, déterminer la puissance dissipée par les forces intérieures.
2
P0
eau à la vitesse V'
eau à la vitesse V
H'
H
x
h