La durée de vie, exprimée en années, d`un composant électronique

Travail facultatif à rédiger sur copie pour le lundi 25 avril 2016
Exercice 1.
La durée de vie, exprimée en années, d’un composant électronique peut être modélisée par une variable
aléatoire notée X suivant la loi exponentielle de paramètre λ avec λ > 0.
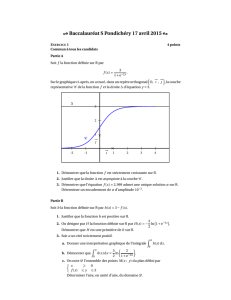
La courbe de la fonction densité associée est représentée en annexe ci-dessous.
1. Sur le graphique de l’annexe :
a. Représenter la probabilité P(X 1).
b. Indiquer où se lit directement la valeur de λ.
2. On suppose que E(X)= 2.
a. Que représente dans le cadre de l’exercice la valeur de l’espérance mathématique de la variable aléatoire X ?
b. Calculer la valeur de λ.
c. Calculer P(X  2). On donnera la valeur exacte puis la valeur arrondie à 0,01 près. Interpréter ce résultat.
d. Sachant que le composant a déjà fonctionné une année, quelle est la probabilité que sa durée de vie totale soit
d’au moins trois années ? On donnera la valeur exacte.
Partie C
Un circuit électronique est composé de deux composants identiques numérotés 1 et 2. On note D1 l’évènement
« le composant 1 est défaillant avant un an » et on note D2 l’évènement « le composant 2 est défaillant avant
un an ». On suppose que les deux évènements D1 et D2 sont indépendants et que P (D1) = P (D2) = 0,39.
Deux montages possibles sont envisagés, présentés ci-dessous :
1. Lorsque les deux composants sont montés « en parallèle », le circuit A est défaillant uniquement si les deux
composants sont défaillants en même temps.
Calculer la probabilité que le circuit A soit défaillant avant un an.
2. Lorsque les deux composants sont montés « en série », le circuit B est défaillant dès que l’un au moins des
deux composants est défaillant. Calculer la probabilité que le circuit B soit défaillant avant un an.
ANNEXE :

Exercice 2.
Soit un cube ABCDEFGH d’arête 1.
Dans le repère
, , ,A AB AD AE
, on considère les points M, N et P de coordonnées respectives
3 1 5
1;1; , 0; ;1 , 1;0;
4 2 4
M N P
1. Placer M, N et P sur la figure donnée en annexe.
2. Déterminer les coordonnées des vecteurs
et MN MP
. En déduire que les points M, N et P ne sont pas alignés.
3. On considère l’algorithme 1 donné en annexe.
a. Exécuter à la main cet algorithme avec les coordonnées des points M, N et P données ci-dessus.
b. À quoi correspond le résultat affiché par l’algorithme ? Qu’en déduire pour le triangle MNP ?
4. On considère l’algorithme 2 donné en annexe. Le compléter pour qu’il teste et affiche si un triangle MNP est rectangle
et isocèle en M.
5. On considère le vecteur
5; 8;4n
normal au plan (MNP).
a. Déterminer une équation cartésienne du plan (MNP).
b. On considère la droite  passant par F et de vecteur directeur
n
. Déterminer une représentation paramétrique de la
droite .
6. Soit K le point d’intersection du plan (MNP) et de la droite .
a. Démontrer que les coordonnées du point K sont
4 24 23
;;
7 35 35
b. On donne FK =
27
35
. Calculer le volume du tétraèdre MNPF.
ANNEXE :

Corrigé n° 1 ( Antilles juin 2015 – Corrigé APMEP)
c. P(X  2) = 1 – e-0.5 × 2 = 1 – e-1  0.63 au centième près.
Ce résultat est la probabilité qu’un composant ait une durée de vie inférieure à la
durée moyenne.
d. On nous demande : P(X1) (X3).
En appliquant la propriété de durée de vie sans vieillissement, on obtient :
P(X1) (X3) = P ( X  2) = e- 0.5 × 2 = e- 1  0.368
Partie C
Corrigé n° 2 (Pondichery – Avril 2015 – Corrigé APMEP)
Avec ce que l’on a vu en cours avant les vacances :
Soit L le point de coordonnées
4 24 23
;;
7 35 35
.
100 192 92
5 8 4 0
35 35 35
L L L
x y z     
donc L  (MNP)
Pour savoir si L   on résout le système :
43
15
7 35
24 3
8
35 35
23 3
14
35 35
tt
tt
tt
Le système admet une solution donc L  .
De plus par définition,  est perpendiculaire au plan (MNP) donc sécante avec (MNP).
Le point d’intersection K a bien pour coordonnées
4 24 23
;;
7 35 35
.

Autre méthode :
Le point d’intersection K a bien pour coordonnées
4 24 23
;;
7 35 35
.
Algorithme 2 :