Algorithmique entre programmation et démarche

f
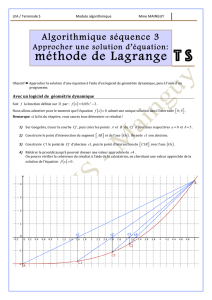
[−2; 1] f(x) = 2x3−3x2−6x
f[−2; 1]
x−2x0
f(x0)
% &
−16 −7
x0

a=−2b= 1 [a;b]
u=−1v= 0 f(u)f(v)
[a;b]x0
[a;b]
x0
x0
x0
[a;b]
u v
f(u)f(v)
f(u)< f(v)a u
f(u)> f(v)b v
f(u) = f(v)a u b v
a−b
≥
←
←
←
≤ ←
≥ ←
[a;b]
u=2a+b
3v=a+2b 3
u−v≥e
f(u)f(v)
f(u)< f(v)a u
f(u)> f(v)b v
f(u) = f(v)a u b v
u−v < e [u;v]
[a;b] [a;u] [u;v]
[v;b]f(u)< f(v)
a u f(u)> f(v)
b v a u
b v
u v
a−b
u v
?
?

•
?
•
•
•
•
?
%
%
•

?
?
?
?
?
?
(Q, Γ, B, Σ, q0, δ, F )
Q
Γ
B∈Γ
Σ (Σ ⊆Γ− {B})
q0∈Q
δ:Q×Γ→Q×Γ× {←,→}
F⊆Q