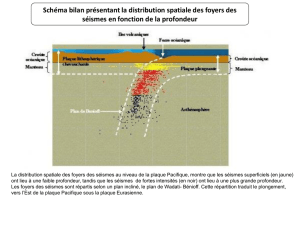
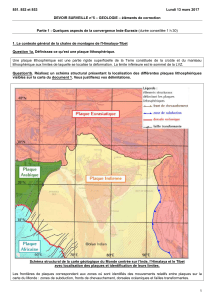
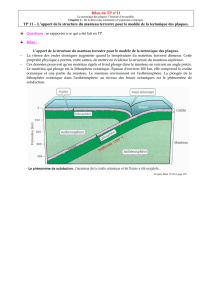
DS 5 20142015 Dynamique enveloppes et manteau - bcpst-svt-parc

1
851. 852 et 853 D.S. n°5 Géologie – éléments de correction 09/03/2015
Partie 1 : Gravimétrie et isostasie (20 points)
Exercice A : En milieu continental
1. Définir l’anomalie de Bouguer et indiquer sa méthode d’obtention, puis interpréter les valeurs observées
en Scandinavie (Document 1).
L’anomalie de Bouguer résulte d’une confrontation entre la valeur de g mesurée en un point de latitude et d’altitude
données, et celle calculée à la même latitude mais à l’altitude 0, sur l’ellipsoïde de référence (= de Clairault).
Au préalable, la valeur de g mesurée doit être successivement corrigée :
- des effets de l’altitude : correction à l’air libre,
- des effets des masses situées entre le point de mesure et l’ellipsoïde de Clairault : correction de plateau,
- des effets des reliefs voisins : correction topographique.
Une fois ces corrections effectuées, la différence entre « g mesurée corrigée » et « g calculée » est appelée
anomalie de Bouguer.
Une anomalie de Bouguer positive signale un « excès » de masse (sous-entendu, excès par rapport à la Terre de
référence, qui correspond au modèle PREM), c’est-à-dire des matériaux de masse volumique supérieure à ce que
prédit PREM.
Inversement en ce qui concerne les anomalies négatives.
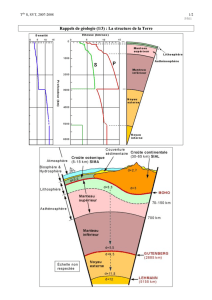
La carte 1b de l’anomalie de Bouguer en Scandinavie montre des valeurs négatives (-30 à -130 mgal) au niveau des
reliefs montagneux indiqués par la carte topographique 1a : il existe un déficit de masse, que l’on peut interpréter
comme la présence d’une racine crustale sous ces reliefs (la croûte, moins dense que le manteau, occupe un
volume « normalement » occupé par du manteau).
2. Expliquer comment on utilise les données du document 2a pour déterminer les anomalies isostatiques
puis interpréter les anomalies constatées en Scandinavie (document 2b).
La profondeur du Moho indique la base de la croûte. Sur la carte 2a sont indiquées la profondeur du Moho déduite
du modèle d’Airy selon lequel un relief est compensé en profondeur par une racine crustale comme indiqué plus
haut, et le Moho sismique repéré grâce à la technique de sismique réflexion. On constate que les données ne
coïncident pas bien, le Moho sismique apparaît plus profond que le Moho calculé, en particulier au niveau du Golfe
de Bothnie. La base de la croûte étant plus profonde qu’attendu, on peut en déduire que l’équilibre isostatique n’est
pas réalisé.
La prise en compte du Moho calculé avec le modèle d’Airy permet de calculer une correction isostatique – qui prend
en compte le déficit de masse lié à l’épaisseur anormalement importante de la croûte – qui permet de corriger
l’anomalie de Bouguer. La valeur obtenue constitue alors l’anomalie isostatique. Si sa valeur diffère de zéro, cela
signifie que l’équilibre isostatique n’est pas réalisé, comme le suggèrent les données du document 2a.
La carte 2b des anomalies isostatiques montre des anomalies négatives fortes, en particulier au niveau du Golfe de
Bothnie : l’équilibre isostatique n’est pas réalisé dans ces zones, et son signe négatif indique que la région, encore
en cours de rééquilibrage, se soulève.
Cela peut être mis en relation avec la disparition de la calotte glaciaire depuis 8000 ans : une surcharge a disparu,
elle enfonçait la lithosphère dans l’asthénosphère

2
3. Calculez la position attendue du Moho à Briançon, ville située à 1 326 m d’altitude, en supposant que cette
portion de lithosphère est à l’équilibre, et que la croûte continentale possède une densité homogène.
Soit h l’altitude du secteur de Briançon et H’ l’épaisseur totale de la croûte continentale à ce niveau.
On peut représenter la situation de Briançon comme suit, en comparaison avec une croûte continentale
« moyenne » d’altitude 0 et d’épaisseur H : si la croûte continentale est à l’équilibre, l’altitude h est compensée par
l’existence d’une racine d’épaisseur R, dont il faut calculer la valeur.
L’écriture des conditions de l’équilibre isostatique sur la surface de compensation amène l’égalité suivante :
ρ
c
.H + ρ
m
.R = ρ
c
.H’ = ρ
c
.(h + H + R)
R (ρ
m
– ρ
c
) = h.ρ
c
R = h.ρ
c
/ (ρ
m
– ρ
c
)
A.N. : R = 1 326 x 2,7 / (3,2 – 2,7) = 7 160 m
La profondeur du Moho devrait donc être égale à h + H + R = 1 326 + 30 000 + 7 160 = 38 486 m soit environ 40 km.
4. En utilisant les informations fournies par le document 3 :
a. Indiquez si la valeur utilisée pour la masse volumique de la croûte continentale dans le calcul
précédent est plausible.
On a utilisé une valeur de densité égale à 2,7 pour la croûte continentale et supposé que cette valeur était
homogène.
- au vu du document 3b, les masses volumiques crustales ne sont pas homogènes mais augmentent avec la
profondeur,
- par contre, la valeur de 2,7 est plausible, car semblant correspondre à la moyenne entre les valeurs minimales
(2,4) et maximale (3,1).
b. Confrontez la position du Moho calculée précédemment à celle proposée dans le modèle.
Dans ce contexte, la profondeur du Moho semble bien estimée (en effet, le document 3b montre bien une
profondeur du Moho de l’ordre de 40 km dans le secteur de Briançon).
5. En supposant que seule l’érosion intervient, calculer en combien de temps le secteur de Briançon
atteindra 500 m d’altitude.
Attention quand on dit que seule l’érosion intervient, c’est que l’on ne prend pas en compte les processus
tectoniques qui pourraient contribuer à des mouvements verticaux de la croûte !
Si l’altitude est égale à 500 m, la racine a une épaisseur R = h.ρc / (ρm – ρc) soit R = 2,7 km.
[Gagner du temps en reprenant la formule établie à la question 3 !]
La nouvelle épaisseur de croûte sera égale à h + H + R = 0,5 + 30 + 2,7 = 33,2 km
L’érosion aura donc dû dégager une hauteur de 38,5 – 33,2 = 5,3 km de matériaux rocheux.
A raison de 0,5.10
-6
km/an, le secteur atteindra l’altitude de 500 m en 10,6 millions d’années.
ρ
c
ρ
c
h
H
R
Surface de compensation
H’

3
6. Calculer la hauteur de sédiments déposés correspondant au matériel érodé.
Le volume total érodé est égal (en km
3
) à : 5,3 x 100 x 20 = 10 600 km
3
Ces matériaux, à l’origine, avaient une densité égale à 2,7. Une fois redéposés sous forme de sédiments, leur
densité moyenne est de l’ordre de 2,0.
Puisque la densité a diminué, le volume a augmenté ; il a augmenté d’un facteur 2,7/2 = 1,35
Le volume de sédiments déposé est donc égal à 10 600 x 1,35 = 14 310 km
3
Ce volume se répartit sur une surface de 100 / 80 = 8 000 km²
La hauteur de sédiments déposés est donc égale à 14 310 / 8 000 = 1,8 km
7. Calculer la subsidence occasionnée par le dépôt des sédiments dans le bassin sédimentaire.
Comparons la situation de la croûte d’épaisseur H avant le dépôt des sédiments et après le dépôt avec le
réajustement isostatique (qui entraîne une subsidence X)
L’écriture des conditions de l’équilibre isostatique sur la surface de compensation amène l’égalité suivante :
ρc.H + ρm.x = ρs.hs + ρc.H
x = ρs.hs / ρm
A.N. : x = 2 x 1,8 / 3,2 = 1,1 km
Le dépôt de 1,8 km de sédiments imposerait une subsidence de 1,1 km.
Exercice B : en milieu océanique
1. Représenter l’épaisseur de la lithosphère sur une coupe au travers d’un océan possédant les
caractéristiques suivantes :
marge passive dorsale marge active
2. Indiquer quelle est la profondeur moyenne des dorsales, celle des plaines abyssales.
Dorsales : 2 500 m
Océans : 4 000 m
ρ
c
ρ
c
ρ
s
Surface de compensation
H
x
H
h
s

4
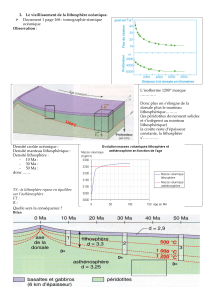
3. Nommer et expliquer le phénomène responsable de la variation de profondeur du plancher océanique
observée depuis la dorsale jusqu’aux abysses.
La lithosphère océanique est d’épaisseur nulle au niveau des dorsales : l’isotherme 1300°C affleure à la surface du
plancher océanique. Plus la lithosphère est éloignée de la dorsale, plus l’isotherme 1300°C est profond : plus la
lithosphère est épaisse, en raison de l’ajout d’une « semelle » de manteau lithosphérique (qui se forme en raison du
refroidissement du sommet de l’asthénosphère). En conséquence, sa densité augmente puisque la croûte, moins
dense que le manteau, représente une proportion de plus en plus faible dans la colonne de lithosphère. Cette
augmentation de densité entraîne une subsidence qui explique l’augmentation progressive de la profondeur du
plancher océanique. Il s’agit d’une subsidence thermique.
4. En utilisant les données précédentes, calculer quelle devrait être la hauteur totale de l’édifice volcanique
qui constitue cette île.
L’île est installée sur une portion de lithosphère de 25 Ma, dont le toit devrait donc être à :
P = 350 x √25 + 2 500 = 4 250 m.
La hauteur totale de l’édifice devrait être égale à 4 250 + 2 000 = 6 250 m
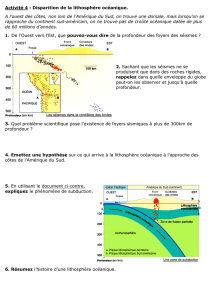
5. A partir de l’analyse de ce document, indiquer quel est l’effet d’un édifice volcanique sur la lithosphère
océanique qui le supporte.
L’anomalie gravimétrique à l’air libre (= g mesuré seulement corrigé des effets de l’altitude du point de mesure – g
0
)
rend compte de la topographie. On constate des anomalies négatives (jusqu’à -160 mgal) en auréole autour des
édifices volcaniques, qui coïncident avec des profondeurs de l’ordre de – 5 000 à – 6 000 m sur la carte
topographique. Cela suggère que les édifices volcaniques sont responsables d’un enfoncement de la lithosphère
océanique qui les supporte en raison de la surcharge qu’ils exercent.
6. On cherche à prendre en compte cet effet. En appliquant le modèle d’Airy, calculer la nouvelle hauteur totale
de l’île précédemment étudiée (question 4). Pour cela, on assimile le volcan à un parallélépipède et on suppose
que la masse volumique des matériaux de l’édifice volcanique est identique à celle de la croûte océanique.
Commenter le résultat obtenu et proposer une explication.
Le poids de l’île engendre une subsidence supplémentaire, que l’on peut calculer en appliquant le modèle d’Airy :
Sur la surface de compensation, l’écriture des conditions d’équilibre donne :
P.ρe + hco.ρco + x.ρm = H.ρco + hco.ρco
(on suppose que la masse volumique des matériaux de l’édifice volcanique ρc est identique à celle de la croûte
océanique ρco)
Soit :
P.ρe + x.ρm = (h + P + x).ρco
ρ
e
ρ
co
ρ
m
ρ
c
ρ
co
h
surface de compensation
édifice volcanique de hauteur
H = h + P + x
P
h
c
o
x
h
c
o

5
x (ρm - ρco) = h.ρco + P(ρco - ρe)
x = [h. ρco + P(ρco - ρe)] / [ρm - ρco]
AN : x = [2 x 2,9 + 4,25 x (2,9 - 1)] / (3,2 – 2,9) = 46,25 km
La subsidence x devrait être de 46,25 km, donc l’édifice volcanique devrait avoir une hauteur H de plus de 50 km !
Ce résultat est évidemment incohérent : il résulte du fait que nous avons appliqué les lois de l’isostasie comme si la
surcharge volcanique se répartissait sur une surface suffisamment grande pour que l’ensemble de la lithosphère
subisse une subsidence généralisée. En réalité, la surcharge due à l’édifice volcanique n’engendre une subsidence
que très localement, qu’à proximité de l’île.
Autrement dit, la hauteur de l’édifice volcanique devrait effectivement être supérieure à celle calculée à la question 4
(soit 6,25 km), mais il nous est impossible de la calculer (il faudrait connaître les lois de la déformation élastique de
la lithosphère pour calculer la subsidence réelle). Nous considèrerons donc que l’édifice volcanique fait bien un peu
plus de 6 km de hauteur.
7. En s’appuyant sur les principales caractéristiques morphologiques de ces îles, expliquer leur évolution.
Le cliché a montre une île volcanique dont le volcan est encore actif, il s’agit d’un édifice « jeune ». Comme cette île
volcanique est alignée avec les deux autres, cela suggère qu’elles résultent d’un volcanisme de point chaud.
Sur le cliché b, le relief de l’île semble moins élevé, la présence de vallées incisées suggère que l’érosion modèle le
relief et l’aplanît progressivement. D’autre part, l’île est entourée par un récif de corail, qui exige entre autres des
eaux peu profondes pour se développer : les rivages de l’île ont permis la mise en place de ces récifs. L’île étant
plus âgée que la précédente, elle illustrerait une étape ultérieure dans l’évolution d’une île volcanique intra-
océanique.
Sur le cliché c, on observe un récif en « couronne » qui entoure un lagon, mais il n’y a pas trace d’édifice volcanique.
Or cet édifice est plus âgé que les précédents. On peut faire l’hypothèse qu’il représente une étape encore plus
tardive, avec disparition du relief volcanique en raison de la subsidence thermique du plancher océanique. En
revanche, le développement de coraux leur permet de se maintenir à la profondeur qui leur convient, ils forment un
récif barrière qui délimite un lagon : l’édifice est devenu un atoll.
Voir l’animation de l’évolution en atoll sur la page wikipedia : http://fr.wikipedia.org/wiki/Atoll
8. Commenter la morphologie de cet édifice et proposer une explication à celle-ci.
Cet édifice sous-marin présente une forme de cône tronqué, qui suggère qu’il s’agit d’un édifice volcanique dont le
sommet aurait été arasé par l’érosion, avant qu’il soit englouti dans les eaux océaniques en raison de la susbsidence
thermique.