Vérification Qualitative

Vérification Qualitative
Franck Cassez
IRCCyN/CNRS UMR 6597
BP 92101
1 rue de la Noë
44321 Nantes Cedex 3 France,
email : [e-mail]
RÉSUMÉ. Ce document est une introduction rapide au domaine de la modélisation et de la vérification des applications concur-
rentes. On y présente un modèle permettant de décrire de telles applications : les systèmes de transitions. Les logiques tempo-
relles LTL et CTL sont ensuite introduites pour spécifier les propriétés de ces systèmes. Enfin, les principes des algorithmes de
model-checking pour LTL et CTL sont donnés.
ABSTRACT. In this paper we give a quick overview of the area of modelling and verification of concurrent systems. We take
transition systems as the basic model of concurrent systems, and introduce the temporal logics LTL and CTL. Moreover we give
some hints for the model-checking algorithms for LTL and CTL.
MOTS-CLÉS : système de transitions, logique temporelle, model-checking.
KEYWORDS: transition systems, temporal logics, model-checking
1. Introduction
Dans ce document on introduit le domaine de la modélisation et de la vérification des applicationsconcurrentes.
Le contenu est fortement inspiré de [SCH 99] et le lecteur intéressé pourra consulter cet excellent livre où il
trouvera toutes les informations lui permettant d’aller plus loin.
Le but de la vérification est d’assurer qu’un programme (ou système) satisfait un certain nombre de propriétés.
Pour cela il est nécessaire de modéliser formellement le comportement du programme : nous introduisons dans la
Section 2 les systèmes de transitions (finis) qui permettent de décrire des applications concurrentes. Dans la Sec-
tion 3 on introduit les logiques temporelles LTL et CTL qui sont des langages de spécification des propriétés. Une
fois le système décrit par un système de transitions, et les propriétés souhaitées spécifiées en logique temporelle, il
existe un algorithme dit de model-checking permettant de répondre automatiquement à la question : «est-ce que le
système satisfait les propriétés souhaitées?». La Section 4 décrit les principes des algorithmes de model-checking
pour LTL et CTL.
2. Modélisation des systèmes concurrents
La première étape dans la vérification formelle d’un système est la construction d’un modèle formel du compor-
tement de l’application. Des langages de spécification de haut niveau pour les applications concurrentes existent
depuis les années 80 [BOU 91, CAS 87, Le 91, ELL 85]. Certains de ces langages sont maintenant utilisés dans
le cadre de développements industriels. Cependant la sémantique de ces langages est très souvent donnée en terme
de systèmes de transitions [ARN 92] qui sont des machines à états dont le fonctionnement est très simple. On va
donc décrire ces systèmes de base. En composant ces systèmes (par synchronisation) il est possible de décrire des
comportements complexes d’activités concurrentes.

École d’été Temps-Réel 2003.
012
3
45
in-card valide
code-not-OK
code-OK
out-card
take
out-card
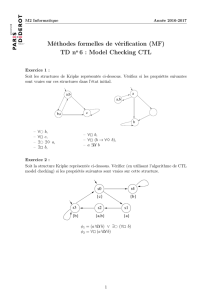
Figure 1. Système de transitions représentant le fonctionnement d’un GAB
2.1. Systèmes de transitions
Définition 1 (Système de transitions [ARN 92]) Un système de transitions Sest un tuple (Q, s0, A, −→)tel
que :
–Qest un ensemble (fini) d’états,
–s0∈Qest l’état initial,
–Aest un alphabet (fini) d’actions,
–−→⊆ Q×A×Qest la relation de transition de S. On note sa −→ s0si (s, a, s0)∈−→.
Une exécution σde Sest une séquence de transitions σ=s0
a0
−→ s1. . . sn
an
−−→ sn+1 . . . telle que ∀i≥
0,(si, ai, si+1)∈−→.a0a1···an··· est la trace de σnotée Tr(σ). Une exécution est finie si la séquence qui
la compose est finie. On note s0
w
−→ s,w∈A∗s’il existe une exécution finie dans Smenant de s0àset de trace w.
Run∗(S)est l’ensemble des exécutions finies de Set Runω(S)l’ensemble des exécutions infinies. Un état s∈Q
est accessible dans Sssi ∃w∈A∗, s0
w
−→ s. Reach(S)est l’ensemble des états accessibles dans Sà partir de
s0: Reach(S) = {s∈Q, ∃w∈A∗, s0
w
−→ s}. Un système de transitions étiqueté est un système de transitions
muni d’une fonction L:Q→2AP où AP est un ensemble de propositions atomiques;L(s)donne l’ensemble des
propositions que satisfait l’état s. On note (Q, s0, A, −→, L)un système de transitions étiqueté. 
Un exemple de système de transitions modélisant un guichet automatique de banque est donné Figure 1. Dans
ce système l’état initial est 0.
On peut bien entendu ajouter des variables entières ou plus généralement des variables à valeurs dans un
ensemble fini [MAN 91] pour étendre le modèle de la Définition 1. Dans ce cas le nombre d’états du système est
toujours fini. Un exemple de l’utilisation de variables entières est donné dans la Figure 2.
2.2. Synchronisation de systèmes de transitions
Un système concurrent est en général constitué de plusieurs composants interagissants. Pour décrire les inter-
actions on utilise la notion de produit synchronisé à la Arnold-Nivat [ARN 92]. Pour modéliser le fonctionnement
asynchrone des systèmes on introduit une action spéciale •qui indique qu’un système ne «fait rien pendant que
d’autres changent d’état».
Définition 2 (Produit synchronisé [ARN 92]) Soient nsystèmes de transitions Si= (Qi, si
0, Ai,→i), i ∈[1, n],
et I⊆A1∪ {•} × A2∪ {•} × · · ·× An∪ {•} une contrainte de synchronisation. Un élément (a1, a2, . . . , an)de I
est appelé un vecteur de synchronisation. Le produit synchronisé (S1kS2· · · k Sn)Ides nsystèmes de transitions
Siavec la contrainte Iest le système de transitions S= (Q, s0, A, →)défini par :
–Q=Q1×Q2× · · · × Qn,
–s0= (s1
0, s2
0,...,sn
0),
–A=A1∪ {•} × A2∪ {•} × · · · × An∪ {•},

Vérification qualitative
–−→⊆ Q×A×Qest telle que :
(q1,...,qn)(a1,...,an) −−−−−−→ (q0
1,...,q0 n)⇐⇒ ∀i∈[1, n],(si ai∈Ai, qi
ai
−→ q0
i
sinon ai=•et qi=q0
i
Ce type de synchronisation permet de décrire des envois/réceptions de messages (par exemple sur la Figure 2
et Figure 3 les !et ?représentent les émissions et réceptions de messages). Un exemple de contrainte de syn-
chronisation pour les automates des Figure 2 et Figure 3 est donné dans la Table 1. Sur cet exemple on choisit
de renommer les vecteurs de synchronisation : on a ainsi une synchronisation à la Arnold-Nivat avec renommage.
Formellement il suffit d’étendre la Définition 2 ainsi : au lieu de I, on utilise une fonction partielle fde synchro-
nisation f:A1∪ {•} × A2∪ {•} × · · · × An∪ {•} −→ A(où Aest un nouvel alphabet) et
(q1,...,qn)b −→ (q0
1,...,q0 n)⇐⇒ 
f(a1,...,an) = b
∧∀i∈[1, n],(si ai∈Ai, qi
ai
−→ q0
i
sinon ai=•et qi=q0
i
Avec une fonction de renommage comme celle de la Table 1 le produit synchronisé des automates des Figure 2
et Figure 3 est celui de la Figure 4.
f(?in-card,!in-card) = in
f(?valide,!valide) = valide
f(!out-card,?out-card) = out
f(?take,!take) = take
f(code-OK, •) = code-OK
f(code-not-OK, •) = code-not-OK
f(keep-card, •) = keep-card
Tableau 1. Contrainte de synchronisation pour le GAB
0 1 2
3
45
?in-card ?valide ∧n:= n+ 1
code-not-OK ∧n≤3
code-not-OK
∧n > 3
code-OK
!out-card
?take
n:= 0 keep-card
n:= 0
Figure 2. Un GAB avec messages
2.3. Propriétés des exécutions d’un système de transitions
Blocage.
Un état deadlock (bloquant) d’un système de transitions Sest un état qui n’est source d’aucune transition. Une
propriété importante que l’on souhaite souvent assurer dans un système de transitions est l’absence de deadlock

École d’été Temps-Réel 2003.
0123
!in-card !valide ?out-card
!take
Figure 3. Un utilisateur du GAB
(0,0) (1,1)
in (2,2)
(4,2)(5,3)
(3,2)(0,2)
(1,2)
valide
code-OK
out
take
code-not-OK
n > 3
keep-card
code-not-OK
n≤3
Figure 4. Produit synchronisé GAB ×U – contrainte I
(car ces états correspondent à des blocages non voulus). Mais certains états du système correspondant à la fin de
l’exécution de l’application sont alors considérés comme des deadlocks. Il est donc nécessaire de distinguer les
blocages non souhaités de ceux qui correspondent à la fin de l’exécution du système. Ceci est possible en utilisant
la fonction d’étiquetage (Cf. Définition 1) et en étiquetant les états de fin d’exécution par une propriété terminal.
Les vrais états deadlock sont alors les états bloquants qui n’ont pas la propriété terminal.
Équité.
Une autre propriété importante d’une exécution d’un système de transitions est l’équité [ARN 92, SCH 99,
EME 90]. On considère dans ce cas que toutes les exécutions sont infinies (au besoin on les complète par des
transitions •). On dit qu’une transition d’étiquette aest tirable à partir d’un état ssi ∃s0|(s, a, s0)∈−→. La notion
d’équité vise à définir un sous ensemble de l’ensemble des exécutions d’un système de transitions de façon à
éliminer les exécutions non réalistes. Par exemple si l’on considère deux systèmes de transitions S1et S2que l’on
synchronise, dans le produit synchronisé il peut y avoir des exécutions qui à partir d’un certain point ne contiennent
que des transitions d’étiquette (a, •): le système S2ne fait rien alors que potentiellement une transition (x, b)est
tirable. Si l’on considère que cette exécution est irréaliste il faut pouvoir la caractériser.
Un premier critère d’équité est celui de l’équité forte : une exécution σsatisfait le critère d’équité forte ssi toute
transition infiniment souvent tirable est infiniment souvent tirée. Un critère plus faible est celui de l’équité faible :
une exécution σsatisfait le critère d’équité faible ssi toute transition toujours tirable à partir d’un certain point est
infiniment souvent tirée. L’équité forte implique l’équité faible.
2.4. Propriétés des systèmes de transitions
Déterminisme.
Un système de transitions S= (Q, s0, A, →)est déterministe ssi
∀s, s0, s00 ∈S, ∀a∈A, s a −→ s0∧sa −→ s00 =⇒s0=s00
Sinon il est non déterministe. Ceci implique que pour une trace donnée il n’y a qu’une seule exécution possible.
Il n’est pas nécessaire qu’un système de transitions soit déterministe pour être un modèle correct. Le non déter-
minisme permet de représenter plusieurs choix possibles ou des parties de l’application pour lesquelles plusieurs
comportements sont possibles sans que l’on sache ou que l’on veuille les modéliser de façon précise.

Vérification qualitative
Équivalence de systèmes de transitions.
A partir d’un système de transitions S= (Q, s0, A, −→)on définit l’ensemble des traces finies de S(le
langage de S) par L∗(S) = {Tr(σ), σ ∈Run∗(S)}. L’ensemble des traces infinies Lω(S)es l’ensemble des traces
des exécutions infinies : Lω(S) = {Tr(σ), σ ∈Runω(S)}.
Un autre point de vue peut être adopté : un système de transitions définit implicitement un arbre d’exécu-
tion qui correspond au dépliage de ce système à partir de l’état initial. L’arbre d’exécution A(S)de Sest défini
inductivement par :
1) s0est la racine de A(S);
2) si sest un nœud de A(S)et sa −→ s0alors s0est un fils de s.
Un tel arbre1est en général infini (sauf si toutes les exécutions sont finies). Tout chemin dans l’arbre à partir de la
racine correspond à une exécution de S.
A partir de ces notions on peut parler d’équivalences de systèmes de transitions.
Deux systèmes de transitions S1= (Q1, s1
0, A, −→1)et S2= (Q2, s2 0, A, −→2)sont trace-équivalents ssi
L∗(S1) = L∗(S2)(une définition similaire est obtenue avec Lω). Ils sont (fortement) bisimilaires ssi A(S1)et
A(S2)sont isomorphes.
La notion de bisimulation est très importante et indique que si S1et S2sont bisimilaires, S1peut mimer chaque
action de S2(et réciproquement) et donc ces deux systèmes sont indiscernables par un observateur qui ne voit que
les actions.
Définition 3 (Relation de bisimulation) Soit S= (Q, s0, A, →)et S0= (Q0, s0
0, A, →)deux systèmes de transi-
tions2et R ⊆ S×S0.Rest une relation de bisimulation ssi ∀s∈S, s0∈S0, sRs0implique
∀a∈A, s a −→ s1=⇒s0a −→ s0
1∧s1Rs0 1(1)
∀a∈A, s0a −→ s0
1=⇒sa
−→ s1∧s1Rs0
1(2)
Set S0sont en bisimulation ssi il existe une relation de bisimulation Rentre Set S0avec s0Rs0
0. Si on a uni-
quement la contrainte (1) de la Définition 3 alors Rest une relation de simulation entre S0et Set S0simule S.
Si Ssimule S0et S0simule S,Set S0ne sont pas forcément bisimilaires : il est possible que ce soient deux
relations différentes qui permettent les simulations.
La bisimilarité implique l’équivalence de traces. Si les systèmes S1et S2sont déterministes, l’équivalence de
trace implique la bisimilarité. Un exemple de deux systèmes de transitions trace-équivalents mais non bisimilaires
est donné Figure 5.
s0
s1
s2
s3
s4
a
a
b
c
τ
τ
(a) S
s0
0s0 1
s0
2
s0
3
a
b
c
τ
τ
(b) S0
Figure 5. Deux systèmes de transitions non bisimilaires
1. Pour être tout à fait formel, il faudrait distinguer les noms des nœuds des noms des états correspondant à ces nœuds.
2. On utilise le même symbole →pour les deux systèmes bien que ces deux relations soient différentes : le contexte indique
clairement de quelle relation il s’agit.