c Boukaddid TD n˚10 : optique sup2 TSI Formation des images

c
Boukaddid TD n˚10 : optique sup2 TSI
Formation des images-Instruments optiques
Exercice n˚1 :Etude d’un miroir sph´erique (d’apr´es Enac)
Un miroir sph´erique de centre Cet de sommet Sest prolong´e dans un milieu transpa-
rent homog`ene et isotrope d’indice n= 1,tel que l’air .
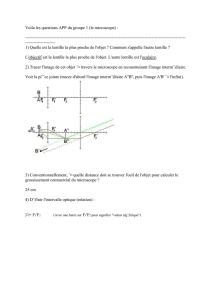
1. Donner les positions des foyers objet F et image F’ du miroir .
2. Quelle doit ˆetre la vergence V d’un miroir sph´erique plac´e dans l’air (n= 1) pour
qu’il donne d’un objet r´eel plac´e `a 10mdu sommet une image droite et r´eduite
dans le rapport 5 ?
3. Quelle est la nature d’un tel miroir ?
4. Un objet est plac´e dans un plan orthogonal `a l’axe optique du miroir passant par
le centre C . O`u se trouve l’mage ?
5. Exprimer dans ce dernier cas le grandissement γ. Connaissez-vous une applica-
tion ?
Exercice n˚2 :T´elescope de Cassegrain (d’apr´es CCP)
•Donn´ees num´eriques :
•Diam`etre de la Lune : DL= 3456km
•Distance Terre−Lune : DT L = 384000km
1. L’axe optique d’un miroir sph´erique concave (M), de sommet S, de centre C et
de rayon R=SC est dirig´e vers le centre de la Lune.
(a) Determiner la position de l’image A0B0de la Lune apr´es r´eflexion sur (M).
(b) Calculer le diam`etre apparent εdu disque lunaire .
(c) En deduire la dimension de l’image A0B0pour |R|= 60 cm.
2. On r´ealise l’objectif d’un t´elescope de type Cassegrain en associant deux miroirs
sph´eriques :
•un miroir sph´erique concave (M1), appel´e miroir primaire, de sommet S1,
de centre C1,de foyer F1et de rayon R1=S1C1.
•un miroir sph´erique convexe (M2), appel´e miroir secondaire, de sommet
S2, de centre C2,de foyer F2et de rayon R2=S2C2.
Le miroir (M1) comprend une petite
ouverture centr´ee en S1pour permettre
le passage de la lumi`ere apr`es r´eflexion
sur (M1) puis sur (M2).Le miroir (M2)
est de petite dimension, afin de ne pas
obstruer le passage de la lumi`ere tom-
bant sur le miroir primaire.
C1C2
S2S1
(M1)
(M2)
F’
(a) O`u doit se situer l’mage A0B0de la Lune apr´es r´eflexion sur (M1), afin que
le miroir sph´erique convexe (M2), caracteris´e par S2,C2et F2, en donne une
image r´eelle A”B” ?
1 / 3

c
Boukaddid TD n˚10 : optique sup2 TSI
(b) D´eterminer la position du foyer image F0, de l’association des miroirs (M1)
et (M2), en exprimant S2F0en fonction de R1,R2et d=S2S1.
(c) Exprimer le grandissement transversal γde l’objet A0B0`a travers le miroir
(M2) en fonction de R1,R2et d=S2S1.
(d) Calculer S2F0,γet la dimension finale de l’image A”B” pour :|R1|= 60
cm ;|R2|= 40cm et d= 18cm .
(e) Quelle serait la distance focale image fLd’une unique lentille mince qui
donnerait de la Lune la mˆeme image A”B” ? Commenter.
Exercice n˚3 :Objectif de photocopieur (D’pr`es V´eto)
Les proc´ed´es actuels de reprographie n´ecessitent la formation de l’image du document
sur une surface photosensible par l’interm´ediaire d’un objectif de reproduction . On
d´esire reproduire un document de format A4 soit en A4 (mˆeme format),en A3 (format
double en surface) ou en A5 (format moiti´e en surface) . On r´ealise ces diff´erentes ti-
rages `a l’aide d’un objectif en modifiant les positions respectives des lentiles `a l’int´erieur
du syst`eme .
La distance entre le document et le
r´ecepteur photosensible est de 384mm
et l’on positionne une premi`ere lentille
divergente L1de distance focale image
f0
1=−90mm `a 180mm du r´ecepteur .
AA’
O1
180mm
384mm
L1
Document R´ecepteur
1. La lentille L1peut-elle donner une image du document sur le r´ecepteur ?Justifier
2. On ajoute alors une lentille mince L0
devant la lentille L1`a 180mm du docu-
ment
(a) La lentille L0peut-elle ˆetre diver-
gente ? Justifier
(b) Calculer la distance focale image
f0de cette lentille L0pour obtenir
une image r´eelle du document sur
le r´ecepteur
(c) En d´eduire le grandissement γ1de
l’association des deux lentilles et
indiquer quel type de tirage per-
mettra cet objectif : transforma-
tion de A4en A3 ou de A4 en A5
AA’
O1
180mm
384mm
L1
Document R´ecepteur
L’
O’
180mm
3. En fait la lentille L0est constitu´ee de deux lentilles accol´ees L2et L3.L2´etant
identique `a L1. Calculer la distance focale image f0
3de la lentille L3Quelle est
la nature de cette lentille mince ?
4. On glisse alors la lentille L3afin de l’accoler `a L1. Montrer que l’image du
document reste sur le le r´ecepteur et calculer le grandissement γ2correspondant
`a l’association de ces trois lentilles ;en d´eduire le type de tirage obtenu .
2 / 3

c
Boukaddid TD n˚10 : optique sup2 TSI
Exercice n˚4 :Lunette de Galil´ee (D’apr`es CCP)
Une lunette de Galil´ee comprend :
•un objectif assimilable `a une lentille mince (L1), de centre O1et de vergence
V1= 5 dioptries
•un oculaire assimilable `a une lentille mince (L2), de centre O2et de vergence
V2=−20 dioptries.
1. D´eterminer la nature et les valeurs des distances focales images f0
1et f0 2des
lentilles .
2. La lunette est du type afocal :
(a) Pr´eciser la position relative des deux lentilles, la valeur de la distance d=
O1O2et l’int´erˆet d’une lunette afocale.
(b) Dessiner, dans les conditions de Gauss, la marche d’un rayon lumineux in-
cident, issu d’un point objet `a l’infini, faisant un angle θavec l’axe optique
et emergeant sous l’angle θ0.
(c) En deduire le grossissement (ou grandissement angulaire) de cette lunette
en fonction des angles θet θ0, puis des distances focales f0
1et f0 2. Valeur du
grossissement ?
3. Un astronome amateur utilise cette lunette, normalement adapt´ee `a la vision
d’objets terrestres, pour observer deux crat`eres lunaires : Copernic (diam`etre :
96 km) et Clavius (diam`etre : 240 km). Rappel : Distance Terre-Lune : DT L =
384000 km.
(a) L’astronome voit-il ces deux crat`eres lunaires :
•`a l’oeil nu ? (Acuit´e visuelle : 3.10−4rad)
•`a l’aide de cette lunette ? Justifier vos r´eponses
4. La plan`ete V´enus, de 12150 km de diam`etre, occultera Jupiter (de diam`etre
145800 km) le 22 novembre 2065.
Notre astronome amateur (qui sera certainement confirm´e), pourra-t-il observer
`a l’oeil nu ou `a l’aide de sa lunette le disque jovien occult´e par V´enus ? Dans
cette configuration, la distance Terre-V´enus sera DT V = 45.106km.
Exercice n˚5 :Etude d’un microscope (D’apr`es CCP)
Un microscope peut ˆetre mod´elis´e par une lentille mince convergente (L1, O1, f0
1=
0,5cm) dite objectif car plac´e pr`es de l’objet,et une lentille mince convergente (L2, O2, f0
2=
2cm)dite oculaire plac´e pr`es de l’Oeil .On donne O1O2= 16cm . L’image finale doit
avoir une position situ´ee entre le P P (dm) et le P R (Dm) de l’oeil de l’observateur
plac´e au foyer image F0
2de l’oculaire.Pour l’oeil normal dm= 25cm et Dm=∞.
1. Faire la construction liant l’objet AB et l’image A0B0dans le cas de la vision sans
accommodation (Dm) de l’oeil normal.
2. Calculer dans les conditions pr´ec´edentes :
(a) Le grandissement lin´eaire de l’objectif
(b) La puissance et le grossissement du microscope
3. (a) Faire d´esormais la construction liant l’objet AB et l’image A0B0dans le cas
d’une vision quelconque .
(b) Calculer la latitude de mise au point ou profondeur de champ de ce micro-
scope pour un oeil normal .
3 / 3