optique réfraction

March 2001
B. Aka, Phys. Chem. News 1 (2001) 47-55 PCN
47
MÉTHODE PHOTOMÉTRIQUE ET DIGITALE
DE DÉTERMINATION DE L’ÉPAISSEUR ET DES CONSTANTES OPTIQUES
D’UNE COUCHE MINCE ABSORBANTE
B. Aka
Département des Sciences et Technologie / Ecole Normale Supérieure - Abidjan
22 BP 1561 Abidjan 22, COTE D'IVOIRE
* Corresponding author. E-mail : [email protected].org
Received 17 February 2001
Abstract
We describe a full method of determining the thickness and the complex refractive index N = n + ik of a thin
absorbing film deposited onto a transparent substrate, from measured values of the normal incidence reflectance
Rexp and transmittance Texp at the wavelength interval 0.3 – 2.5 µm.
The applicability of the method requires the existence of maxima and minima on the Rexp(λ) and Texp(λ)
spectra due to interference phenomena. One distinguishes two spectra regions :
in the weak absorption region where the extrema appear, the corresponding values only of the transmittance
Texp lead to the successive calculation of refractive index n, thickness d and the extinction coefficient k of the
film.
In the high absorption region, the value of the couple (n, k) is calculated by mean of digital treatment using
experimental values Rexp and Texp. The method is applied to a-Si:H samples prepared by Photo-CVD technique.
The thickness d and the value of the couple (n,k) measured at the wavelength λ = 6 328 Å by ellipsometry
technique show a good agreement with the present method.
Keywords: Optical characterization; Reflectance; Transmittance; Refractive index; Absorption coefficient; Ellipsometry; Optical band gap;
Hydrogenated amorphous silicon (a-Si:H).
Résumé
Nous décrivons une méthode complète de détermination de l’épaisseur et de l’indice de réfraction complexe
N = n + ik d’une couche mince absorbante, déposée sur un substrat transparent, à partir des valeurs
expérimentales en incidence normale de la réflexion Rexp et de la transmission Texp, dans la gamme spectrale de
0.3 – 2.5 µm .
La mise en œuvre de la méthode nécessite la présence de maxima et de minima dans les spectres Rexp(λ) et
Texp(λ), due au phénomène d’interférence. On distingue deux régions du spectre :
Dans la zone de faible absorption où apparaissent les extrémums, les valeurs correspondantes uniquement à la
transmission Texp permettent de calculer successivement l’indice de réfraction n, l’épaisseur d et le coefficient
d’extinction k du film.
Dans la zone de forte absorption, la valeur du couple (n,k) est déterminée à l’aide d’un simple calcul
informatique combinant les valeurs expérimentales Rexp et Texp. La méthode est utilisée pour la caractérisation
optique des échantillons de silicium amorphe hydrogéné (a-Si:H) déposés par la technique Photo-CVD.
L’épaisseur d et la valeur du couple (n,k) mesurées à la longueur d’onde λ = 6 328 Å par la technique
d’ellipsométrie montrent le bon accord avec la présente méthode .
Mots clés : Caractérisation optique; Réflexion; Transmission; Indice de réfraction; Coefficient d’absorption; Ellipsométrie; Gap optique;
Silicium amorphe hydrogéné (a-Si:H).
1. Introduction
Le développement des composants électroniques et
photovoltaïques et leur miniaturisation a conduit de
plus en plus à des dépôts de couches minces
d’épaisseur allant de 200 Å à 10 µm et de couches
ultraminces d’épaisseur en deçà de 200 Å.
Les constantes optiques décrivent le comportement
de la matière vis-à-vis d’un rayonnement lumineux, et
leur connaissance est primordiale pour une meilleure
étude des propriétés optiques et électroniques de
ladite matière.
Il existe diverses techniques de détermination de
l’épaisseur d des films et des constantes optiques
représentées notamment par l’indice de réfraction n et
le coefficient d’extinction k [1,2].
Certaines techniques sont limitées uniquement à la
détermination de l’épaisseur, par exemple la méthode
mécanique du profilomètre (ou Talystep), (d≥0.1µm)
la méthode électrique de la mesure de la fréquence de
vibration d’un oscillateur à quartz (d ≥ 50 Å) , les
méthodes optiques telle l’interférométrie de Fizeau
(d≥1µm) [1,3], les méthodes nucléaires telle la
détection des reculs élastiques (ERDA) (d ≥ 0.1µm)
[4,5].
D’autres techniques, notamment photométriques,
permettent de déterminer un ou deux des paramètres

B. Aka, Phys. Chem. News 1 (2001) 47-55
48
n, k, d, connaissant au préalable l’un d’entre eux en
général l’épaisseur d; on peut citer la méthode
d’Abelès et le réfractomètre d’Abbe [1], la
spectroscopie de déflexion photothermique (PDS) [2]
ou même la mesure de la photoconductivité [2,6].
Toutefois, l’ellipsométrie [7,8] permet de mesurer
l’épaisseur d et les contantes optiques n et k, mais très
influencée par l’état de la surface du dépôt et limitée
généralement à certaines longueurs d’onde. Plus la
couche est mince et plus grande est la difficulté
d’extraire avec précision son épaisseur et ses
constantes optiques. La seule mesure des facteurs soit
de réflexion R soit de transmission T ne permet
d’accéder avec précision qu’à un ou deux des
paramètres n, k et d au détriment du troisième. Or les
méthodes existantes, qu’elles soient basées sur la
mesure d’un seul spectre Rexp(λ) ou Texp(λ) ou sur la
mesure des deux spectres, sont partitionnées et
nécessitent pour la plupart la connaissance préalable
de l’épaisseur d [3,6,9–16].
Nous regroupons dans ce travail une méthode
globale non destructive basée sur les mesures
conjointes des spectres de réflexion Rexp(λ) et de
transmission Texp(λ) et qui permet de déterminer avec
précision à la fois l’épaisseur d et les spectres n(λ) et
k(λ) sur toute la gamme spectrale de l’ultraviolet à
l’infrarouge. Un programme informatique associé
complète cette méthode.
La première partie du travail présente la méthode
utilisée qui est mise à profit dans la deuxième partie
pour la caractérisation optique des couches minces de
silicium amorphe hydrogéné (a-Si:H) d’épaisseur
comprise entre 900 Å (= 0.09 µm) et 5 000 Å (= 0.5
µm).
2. Description de la méthode
2.1 Rappel d’optique des couches minces
2.1.1 Les équations de Maxwell
Un flux lumineux pénétrant dans un milieu
conducteur ou semi-conducteur exerce une action sur
les électrons qui sont alors accélérés par le champ
électrique
E
r
de l’onde incidente. Les équations de
Maxwell permettent d’étudier les interactions entre le
rayonnement lumineux et la matière [4,17]
t
B
Erot
δ
δ
−=
r, (1)
t
D
JHrot δ
δ
+= rr , (2)
0=Bdiv
r
, (3)
ρ=Ddiv
r. (4)
Pour un milieu électriquement neutre en volume, ρ
est nulle. En outre, si on suppose que le milieu est
homogène et isotrope, alors
EJ
rr
σ =, (5)
HHB r
rrr
µµµ == 0, (6)
EED r
rrr ε=εε= 0. (7)
B
r
et D
r
décrivent l’action de l’onde sur la matière,
µr = 1 dans un matériau non magnétique et σ = 0 dans
un isolant.
On établit l’équation générale de propagation en
prenant le rotationnel de l’équation (1) et (2)
0
0
2
2
00
2=−−∇
t
E
t
E
Errr
δ
δ
σµµ
δ
δ
εεµµ
r
r
r, (8)
et
0
0
2
2
00
2=
δ
δ
σµµ−
δ
δ
εεµµ−∇ t
H
t
H
Hrrr
r
r
r. (9)
2.1.2 Indice de réfraction n, coefficient
d'extinction k et constante diélectrique ε
Les solutions des équations (8) et (9) sont
représentées respectivement par les deux
composantes spatio-temporelles
E
r
et
H
r
de l’onde
électromagnétique
[
]
trqiEE ω−=
r
r
r
r
.exp
0, (10)
[
]
trqiHH ω−=
r
r
r
r
.exp
0, (11)
de sorte que le vecteur d'onde q
r
soit une grandeur
complexe ( 21 qiqq
r
r
r
+
=
) qui s’exprime sous la forme
scalaire suivante
r
c
q
ε
ω
=, (12)
où la constante diélectrique r
ε
est une
caractéristique du milieu telle que
ωε
σ
εεεε
0
121 ii
r+=+= . (13)
On définit, à partir de la relation (12), un indice de
réfraction complexe N comme suit
r
qc
Nε=
ω
= (14)
avec N = n + ik. (15)
Les composantes de q deviennent alors
c
k
qet
c
n
q
ω
ω
== 21 , (16)
comme
(
)
2
2iknN
r+==ε , par identification
avec la relation (13), il s’en suit que
1
22
ε
=
−
kn , (17)
2
0
2ε=
ωε
σ
=nk , (18)
on en déduit les expressions de n et k en fonction de
ε1 et ε2.
2
2
2
11
2
2ε+ε+ε=n, (19)
2
2
2
11
2
2ε+ε+ε−=k. (20)
Dans le cas d'un isolant (diélectrique parfait), σ = 0 et
par suite k = 0 , alors 1
ε=n ; pour l’air n = 1.
2.1.3 Coefficient d’absorption α
Les solutions de l’équation générale de
propagation (relations 10 et 11) deviennent, en
remplaçant le vecteur d'onde complexe q
r
par ses
composantes réelle 1
q
r
et imaginaire 2 q
r

B. Aka, Phys. Chem. News 1 (2001) 47-55 49
()( )
trqirqEE ω−−= r
r
rr
rr .exp.exp 120 , (21)
()( )
trqirqHH ω−−=
r
r
r
r
r
r
.exp.exp 120 . (22)
L’intensité lumineuse d’une onde est représentée par
son flux moyen rayonné par
).2exp(
2
),(),(
1
)(
2
2
0
0
0
rqE
nc
dttrHtrE
T
rI
T
rr
r
r
r
−
µ
ε
=
∫Λ=
, (23)
où )( HE
r
r
Λ désigne le vecteur de Poynting. On
remarque que le terme
(
)
rq
r
r
.2exp 2
−
traduit l’atténuation
que subit ce flux lors de la traversée d’un milieu le
long d’un parcours r.
Par ailleurs, l'intensité du rayonnement lumineux est
aussi donnée par la loi de Lambert-Bouguer
)exp()( 0rIrI α−= . (24)
I0 étant l'intensité lumineuse incidente. En identifiant
()
rα−exp avec
()
rq
r
r
.2exp 2 − et sachant que
λππωω /22/
2cfetckq === , le coefficient
d'absorption α est alors
λ
π
=
ω
=α k
c
k42 , (25)
relié à ε2 comme suit
cn
ωε
=α 2. (26)
La constante diélectrique ε est généralement
utilisée pour décrire les transitions entre bandes
d’énergie. Dans la pratique, on se sert plus
fréquemment du spectre d'absorption )(
λ
=α f qui
présente la même allure que )(
2λ=ε f dans la région
du spectre où la dispersion de n demeure faible.
2.1.4 Cas d’une couche absorbante sur un
substrat transparent
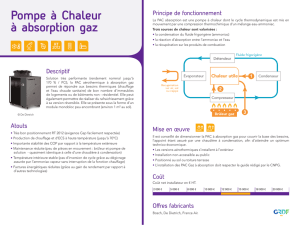
Considérons le film et le substrat homogènes et
d'épaisseur uniforme. L'onde plane incidente à la
surface du film subira des réflexions multiples aux
interfaces 0/1 (air/film), 1/2 (film/substrat) et 2/3
(substrat/air) (Figure 1).
Le film d’épaisseur d et d’indice de réfraction
complexe N1 = n1 + ik1 , peut être considéré comme
situé entre deux milieux transparents qui sont l’air
d’indice de réfraction n0 et le substrat en verre ou en
quartz d’indice n2, puisque l’influence du substrat est
totalement négligeable selon la méthode
expérimentale adoptée dans ce travail.
La sommation des réflexions et transmissions
multiples cohérentes permet la détermination
respectivement de la réflexion en amplitude complexe
totale ℜ et la transmission en amplitude complexe
totale
τ
dont les expressions, dans le cas d’une
incidence normale, sont comme suit [1,3,6,10-12]
1
1
2
1201
2
1201
1δ
α−
δ
α−
+
+
=ℜ j
d
j
d
eerr
eerr , (27)
et
1
1
2
1201
2/
1201
1δ
α−
δ
α−
+
=τ j
d
j
d
eerr
eett , (28)
où rij et tij sont les coefficients de Fresnel aux
interfaces i/j avec
+
=
+
−
=
ji
ij
ji
ji
ij NN
Ni
tet
NN
NN
r,
tels que λ
π
=δ+= dn etiknN jjj
1
1
2 est le déphasage
optique suite à une traversée de la couche d’épaisseur
d. Pour un milieu transparent (non absorbant), k = 0
et N = n.
Figure 1 : Réflexions et transmissions multiples à
travers une couche mince absorbante déposée sur un
substrat transparent (L’intensité lumineuse incidente
I0 est normalisée : I0 = 100 %)
La réflexion R et la transmission T en intensité
sont alors
∗
ℜ
ℜ
=
R, (29)
et
*
0
2ττ= n
n
T. (30)
*
ℜet *
τ sont les expressions conjuguées de
ℜ
et
τ
respectivement.
Les expressions complètes de R et T en fonction
des constantes optiques n0, n1, n2 et k1 s’obtiennent en
remplaçant les coefficients de Fresnel par leurs
expressions [1,10,12]
(
)
()
ψ+ψ++
ψ+ψ++
=ε−α−
α−α−
sincos2
sincos2
2
2
HGeFeE
DCeBeA
Rdd
dd , (31)
avec Ψ = 2 δ1 et n2 = ns
A = [(n1-n0)² + k1² ] [(n1 + ns)² + k1² ]
B = [ (n1-ns)² + k1² ] [(n1 + n0)² + k1² ]
C = (n1² + k1²) (n0² + ns²) – (n1² + k1²)² - n0²ns²
- 4 n0 ns k1²
D = 2 k1 (ns – n0) (n1² + k1² + n0 ns)
et
(
)
)sincos(2
16
2
2
1
2
10
Ψ+Ψ++
+
=α−α−
α−
HGeFeE
eknnn
Tdd
d
s, (32)

B. Aka, Phys. Chem. News 1 (2001) 47-55
50
telles que
E = [ (n1 + n0)² + k1² ] [(n1 + ns)² + k1² ],
F = [ (n1 – n0)² + k1² ] [ (n1 – ns)² + k1² ],
G = - (n1² - n0² + k1²) (n1² - ns² + k1²) + 4n0 ns k1²,
H = 2 k1 ns (n1² - n0² + k1²) + 2 k1 n0 (n1² - ns² + k1²).
Les expressions de R et T ci-dessus sont utilisées
dans la pratique moyennant quelques approximations
selon que la zone spectrale correspond à une région
de faible ou de forte absorption.
2.2 Méthodologie
Les mesures de transmission des films déposés sur
des substrats transparents (quartz ou verre) ont été
effectuées par une méthode différentielle qui consiste
à relever la transmission de la couche sur son substrat
par rapport à un substrat identique servant de
référence. Dans ces conditions, l’influence du substrat
est totalement négligeable sur l’intensité transmise
qui correspond alors uniquement à celle du dépôt.
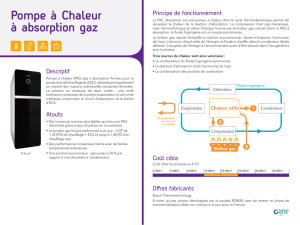
En général, dans la région du spectre où le film est
transparent, R et T présentent des oscillations
graduellement amorties au fur et à mesure que
l'absorption du film augmente (Figure 2).
Figure 2 : Spectre de transmission typique d’une
couche mince absorbante
2.2.1 Région de faible absorption
2.2.1.a Simplification de l’expression de T
En considérant le spectre de transmission T(λ)
dans le domaine où l'absorption demeure faible (en
général pour λ > 1 µm), on peut retenir les
approximations suivantes
k1² << (n1 –n0)² , k1² << (n1 –ns)² et
k1² << (n1 – n0) (n1 – ns) alors H << G, ce qui
conduit à H sin Ψ << G cos Ψ, notamment au
voisinage d’un extrémum où Ψ = (4πn1d / λ) ≈ mπ,
m étant un entier d’ordre.
Dans les cas usuels où n1 > n0 et n1 > ns, alors 4
n0 ns k1² << (n1² - n0²) (n1² - ns²) . Par exemple, dans le
cas du film a-Si:H sur un substrat en verre, on note à
λ ≈ 1 µm : n0 = 1 , n1 ≈ 2.5 , ns = 1.5 , k ≈ 0.01
(Figures 3 et 4, échantillon A), ce qui vérifie bien les
approximations ci-dessus.
Ainsi dans la zone de faible absorption,
l’expression de la transmission T se réduit à [10-12]
() λπ
αα
α
/4cos2
16
121
22
2
2
1
2
10
dneCCeCC
ennn
Tdd
d
s
−−
−
++
=, (33)
où C1 = (n1 + n0) (ns + n1) , C2 = (n1 – n0) (ns – n1)
Le facteur de transmission T atteint des valeurs
maximales et minimales lorsque le produit n1d est
tel que cos (4πn1d / λ) est respectivement égal à +1
et -1. On observe ainsi
un maximum : n1d = 2 P λ / 4, (34)
un minimum : n1d = (2 P + 1) λ / 4, (35)
où P est l'ordre de la frange d'interférence.
2.2.1.b Détermination de l'ordre P d'un extremum
Dans cette région du spectre, la dispersion de n1
(dn1/dλ) reste faible et l'ordre d'un extremum peut
être déterminé à partir des deux premiers maximums
successifs ou à partir des deux minimums successifs,
l'ordre débutant de l'IR vers le visible. Considérons
deux maximums successifs et servons nous de la
relation (34). Si P1 et P2 = P1+1 sont les ordres de ces
2 maximums, on a
n1(λ1).d = P1 λ1 / 2, (36)
n1(λ2).d = P2 λ2 / 2. (37)
Comme n1(λ1) ≈ n1(λ2), on obtient alors
P1 ≈ λ2 / (λ1 - λ2). (38)
Connaissant l'ordre P, on calcule l'épaisseur optique
n1d pour chaque extrémum.
2.2.1.c Détermination de l'indice de réfraction
(Méthode des enveloppes) [10,12].
Dans la zone de faible absorption, lorsque cos
(4πn1d / λ) = ± 1 , l’expression de T (relation 33) se
réduit à
2
21
2
10
)(
16
d
d
s
MAX eCC
ennn
T
α
α
−
−
+
=, (39)
et
2
21
2
10
)(
16
d
d
s
Min eCC
ennn
T
α
α
−
−
−
=. (40)
Dans ce cas, considérons TMAX et TMin comme
deux fonctions continues de λ par le biais de n(λ) et
α(λ), et représentées respectivement par les
enveloppes supérieure et inférieure du spectre de
transmission (Figure 2). Relevons pour la même
longueur d’onde λ les deux valeurs correspondantes à
TMAX et TMin.
En posant X = e- αd et K = 16nonsn1
2, les équations
(39) et (40) peuvent se mettre sous la forme :
02 2
121
22
2=+
−+ CX
T
K
CCXC
MAX
, (41)
02 2
121
22
2=+
+− CX
T
K
CCXC
Min
. (42)
Ces deux relations sont compatibles si
0
11
421 =
−+ X
TT
KCC
MAXMin
. (43)
La résolution de cette équation donne l'expression de
n1
[
]
2/1
2/122
0
2
1)( s
nnn −η+η= , (44)
avec

B. Aka, Phys. Chem. News 1 (2001) 47-55 51
MinMAX
MinMAX
s
s
TT
TT
nn
nn
.
2
20
22
0−
+
+
=
η
. (45)
2.2.1.d Détermination de l'épaisseur d
Connaissant n1d en chaque extremum (relations 34
et 35) et maintenant n1, on calcule la valeur de
l'épaisseur en chaque extremum; la moyenne donnant
la valeur la plus probable de l'épaisseur d ; celle-ci
peut aussi être calculée de la manière suivante
[]
121211
21
).().(2 λλλλ
λλ
nn
d−
Μ
=. (46)
Si la valeur de n1 est quasi-constante dans cette
région spectrale, on peut remarquer que
)(2 121
21
λλ
λ
λ
−
Μ
≈n d, (47)
où M est le nombre d'oscillations entre les extremums
positionnés à 1
λ et à 2 λ (M = 1 entre 2 maximums
ou 2 minimums successifs).
2.2.1.e Détermination du coefficient d'absorption dans
la zone des interférences (Méthode des extremums) [10]
Il s'agit de déterminer le coefficient d'absorption α
en chaque maximum et minimum du spectre de
transmission.
Aux extremums, les relations (41) et (42) s’écrivent,
en respectant l’ordre des signes (+/- ou -/+) avec les
indices (MAX/Min)
0
22
121
22
2=
+
−±+ MAX
T
CXK
MAX
T
CCX
MAX
T
C
MinMinMin
. (48)
La résolution de cette équation en éliminant la
solution X = e αd > 1 (car e- αd est toujours <1)
conduit à la formule (49)
()() []
−+−+
=α 2/1
2
21
2
2121
2
2
222
2
ln
1
MAX
Min
MAX
Min
MAX
Min
MAX
Min
MAX
Min
TCCKTCCKTCC
TC
dmm
(49)
Ce procédé est d'autant plus précis que les extremums
sont moins entassés; aussi, la lecture des grandeurs
TMAX et TMin doit être rigoureuse.
2.2.2 Région de forte absorption
2.2.2.a Méthode digitale pour la détermination de n1,
k1 et α
Lorsque l'absorption du film devient importante,
les phénomènes d'interférence disparaissent et l'effet
des réflexions multiples devient négligeable.
Cette zone, correspondant à l'absorption propre (ou
fondamentale), est caractérisée par αd >> 1 si bien
que la transmission T (relation 32) peut s'exprimer
comme suit [1,12,13,16]
()
[]
()
[]
2
1
2
1
2
1
2
10
2
1
2
10 )(16
knnknn
eknnn
T
s
d
s
++++
+
=
− α
, (50)
de même, la réflexion R (relation 31) peut se mettre
sous la forme simple suivante
(
)
()
2
1
2
01
2
1
2
01
knn
knn
R++
+−
=. (51)
On est alors confronté à la résolution du système
suivant [9,13–15]
Tthéo (n1, k1, d, λ) - Texp = 0, (52)
Rthéo (n1, k1, d, λ) - Rexp = 0, (53)
ou ce qui revient au même à la recherche des couples
de valeurs (n1, k1) appropriées.
Dans ces relations les subscrits "théo" et "exp" se
réfèrent respectivement aux expressions théoriques et
aux valeurs expérimentales.
Ce système est souvent mis sous la forme suivante
() [] () []
)54(
)(16
1
4exp
2
1
2
1
2
1
2
01
2
1
2
10
1
++++
+
=Tknnknn
knnn
n
d
k
s
s
π
λ
()
2/1
2
1
2
exp
exp
exp
exp
11
1
1
1
1
+−
−
+
+
−
+
=k
R
R
R
R
n. (55)
Un simple programme informatique permet de
résoudre ce système d’équations en entrant les
données (λ, Rexp, Texp) relevées sur les courbes
expérimentales Rexp(λ) et Texp(λ) . La valeur de k1 qui
intervient dans le calcul donne n1 et vice-versa.
Quelquefois, plusieurs solutions (n1, k1) peuvent se
présenter pour une valeur λ donnée; cependant, les
valeurs initiales trouvées dans la zone de faible
absorption constituent une référence grâce à laquelle
les solutions aberrantes sont éliminées.
2.2.2.b Calcul de α
Connaissant k1, on calcule le coefficient
d'absorption α dans cette région de forte absorption
en se servant de la relation (25)
λ
π
=α 1
4k.
2.2.3 L’ellipsométrie [7,8]
En général, quand l’angle d’incidence de la
lumière est supérieur à 10 degrés, l'intensité de la
lumière réfléchie dépend de sa polarisation. La
technique ellipsométrique consiste à mesurer
simultanément le rapport des amplitudes Rp et Rs et
leur déphasage ∆. Rp et Rs sont les amplitudes
complexes de l’onde réfléchie selon que le champ
électrique
E
r
de l’onde incidente est orienté
parallèlement ou perpendiculairement au plan
d’incidence
∆∆−∆ Ψ=
ℜ
ℜ
=
ℜ
ℜispi
s
p
s
petge )( . (56)
∆p , ∆s étant le déphasage optique dû à une traversée
du film. Dans la pratique, on mesure les angles
ellipsométriques ψ et ∆ à partir desquels on
détermine, à l’aide d’un programme informatique
associé, à la fois les paramètres d, n et k du film.
Cette technique, très sensible et précise, permet de
réaliser la caractérisation optique de quelques
monocouches déposées sur un substrat (jusqu’à d ≈10
Å); cependant, elle est très influencée par l’état de la
surface (oxyde natif, texture, …).