` ` ffx = + ` 20 fd mm = = `

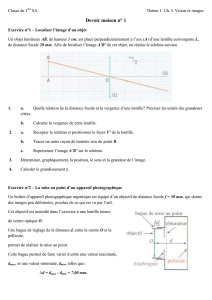
ETUDE OPTIQUE DE L'ŒIL
On étudie ici quelques propriétés de l'œil, organe de la vision. Une
représentation simplifiée est donnée sur la Figure E1.
L'œil comprend :
- le globe oculaire rempli du corps vitré (pour simplifier les
calculs, on prendra son indice n = 1);
- la rétine ou surface sensible de l' œil sur laquelle vient se former
les images des objets observés;
figure E1 : Principe optique de l'œil.
- le cristallin qui pourra être modélisé par une lentille biconvexe, dont la distance focale f ’0 est variable (pouvoir
d'accommodation de l'œil). Sans accommodation, la distance cristallin-rétine d'un œil normal est égale à f’0;
- l'iris qui vient diaphragmer le cristallin en formant la pupille. Cette dernière permet de limiter plus ou moins la quantité de
lumière à pénétrer dans l'œil.
- d'autres éléments nécessaires au bon fonctionnement de cette « mécanique » et qui ne nous concernent pas dans cette modélisation.
On modélisera l'œil par une lentille mince (cristallin), de focale
00
''f f x
(
0
'f
est la focale moyenne et x
 [ -1 mm ; 1 mm ] ) et dont le centre se trouve en un point fixe O de l'axe x'x. La rétine est placée derrière à la
distance d0 du cristallin. Cet œil est utilisé pour observer un objet.
1. L'œil seul : Déterminer, pour un œil normal (
00
' 20f d mm
) le “punctum proximum” dm , c'est à dire la
distance minimale de vision nette d'un objet vertical AB placé sur l'axe x'x.
Interrogez-vous sur l'évolution nécessaire de la focale pour observer la conjugaison entre l'objet qui se rapproche
depuis l'infini et son image fixe sur (E)
2. Défauts de l'œil : Les principaux défauts de l'œil sont, pour un objet placé à l'infini :
- La myopie : L'image se forme avant la rétine (maximum de f ’0 < d0 ). Une lentille biconcave (divergente) permet
de remédier à ce défaut.
- L' hypermétropie : L'image se forme derrière la rétine car l'accommodation est insuffisante (minimum de f ’0 > d0).
Une lentille convergente permet corriger ce défaut.
- La presbytie : Le “punctum proximum” augmente avec l'âge du sujet pour passer de 25 cm (jeune adulte) à 1m
(personne de 60 ans). Cela pose des problèmes pour la lecture. l'utilisation d'une optique convergente permet de
résoudre ce problème.
2.1 .La myopie : - œil non corrigé : On prendra
0
' ' 17f f mm
. Montrer que la vision nette n'est pas possible
pour des objets éloignés. Quelle est la plus grande distance d’m de vision nette (en tenant compte des aptitudes
d'accommodation précédentes) ?
- œil corrigé : Quelle doit être la vergence de la lentille divergente qu'il faut placer devant l'œil, accolée au point O,
pour observer sans accommoder le point de l'infini ? Que devient le “punctum proximum” ?
On s'intéressera à la lentille mince équivalente à l'ensemble des deux lentilles (voir son cours )
2.2. hypermétropie : - œil non corrigé : On prendra
0
' ' 23f f mm
. Montrer que la vision nette n'est pas
possible (même en tenant compte des aptitudes d'accommodation précédentes).
- œil corrigé : Quelle doit être la vergence de la lentille convergente qu'il faut placer devant l'œil, accolée au point
O, pour observer sans accommoder le point de l'infini ? Que devient le “punctum proximum” ?
2.3.presbytie : Le “punctum proximum” est supposé égal à 1m. quelle est la focale de la lentille qu'il faut placer
devant l'œil pour observer un objet placé à 40 cm de O ?

ETUDE OPTIQUE DE L'ŒIL
L'œil est modélisé (Figure C1) par une lentille
mince L0 (cristallin), de centre O, de focale
''
00
f f x
où
'
0
f
est la focale moyenne et
x  [ - = - 1 mm ; = 1 mm] traduit les
capacités d'accommodation. La rétine est un
écran (E) placé derrière à la distance d0 de la
lentille. Cet œil est utilisé pour observer un
objet AB.
1. L'œil seul : Pour un œil normal
'
00
fd
,
c'est à dire que l'image d'un objet à l'infini se
forme sur la rétine (E), l'œil n'a pas besoin
d'accommoder.
Si on rapproche l'objet, et si on veut toujours
avoir l'image sur (E), il faut modifier la focale f
’0, l'œil doit accommoder. Avec une lentille
convergente,
figure C1
lorsque l'objet se rapproche du foyer objet en partant de l'infini, l'image part du foyer image et s'éloigne à l'infini.
Si on veut continuer à avoir une image nette sur (E), il faut que la focale f ’0 diminue. La distance minimale de
vision nette d'un objet vertical AB placé sur l'axe x'x (le “punctum proximum” dm ) correspond à la valeur
minimale de f ’0= d0 - .
00
1 1 1
dd
OA
D'où :
00
()dd
OA 
Le “punctum proximum” est :
00
()
mdd
d
= 380 mm
2. Défauts de l'œil : On considère successivement les défauts suivants :
2.1. La myopie : - œil non corrigé : Le foyer image se trouve maintenant à f ’= 17 mm, donc en avant du plan (E),
par accommodation, a focale peut monter à f ’+  = 18 mm, un objet à l'infini ne pourra pas être observé de façon
nette (Figure C2).
figure C2
figure C3
La plus grande distance d'observation nette est donnée par :
00
1 1 1
dd
OA
soit
0
0
( ' )
'
df
OA fd
= d’m = -
180mm.
Si l'objet se rapproche du foyer objet, comme précédemment, on va observer une limite donnée par :
0
1 1 1
'df
OA
soit
0
0
( ' )
'
df
OA fd
= -80mm.
En résumé : on observera une image nette lorsque la distance d  [ -180mm ; -80mm ]

- œil corrigé : On a maintenant une association de deux lentilles (Figure C2), on peut écrire :
1
1 1 1'
'f OA OA
sommer avec
2
1 1 1'
'' ' f OA OA
pour obtenir
10
1 0 1 0
1 1 1 1 ' '
' ' ' '
'' ff
f f f f
OA OA
La focale de la lentille équivalente doit être égale à d0 (vision à l'infini sans accommodation) lorsque f ’0= f ’:
10
1
''
'''
eq ff
fd
ff
donc f ’1 = d0f ’ / (f ’ – d0 ) la focale est f ’1 = d0f ’ / (f ’ – d0 ) = - 113 mm et la vergence V
= - 8,85 
Cette lentille équivalente a également une focale variable :
1 0 0 0
1 0 0 0 0
' ' ' '
'' ' ' ' '
eq f f f f d
ff f d f f f d
On obtient donc pour les valeurs maximum et minimum de f ’0 : f ’eq,max = 21,40mm , f ’eq,min = 18,63mm
Le “punctum proximum” est donné par :
0 ,min
1 1 1
''eq df
OA
d'où la nouvelle valeur dm = 272 mm.
2.2. hypermétropie : - œil non corrigé : Le foyer image d'un objet à l'infini se trouve maintenant à f’= 23 mm,
donc en arrière du plan (E), par accommodation, la focale peut descendre à f ’- = 22 mm, un objet à l'infini ne
pourra pas être observé de façon nette (Figure C3).
Le domaine de vision nette est donnée par :
0
1 1 1 1
''f d f
OA
soit 220mm =
00
00
( ' ) ( ' )
'
''
d f d f
OA
f d f d
=120mm
On constate que OA est positif, l'objet doit donc être virtuel. La vision nette n'est donc pas possible.
En résumé : on observera une image nette lorsque la distance d  [ 120 , mm , ; , 220 , mm ]
- œil corrigé : On a maintenant une association de deux lentilles (Figure C3), dont le calcul de la focale équivalente
se calcule comme fait précédemment et conduit au résultat :
''
10
''
10
11
'' ff
ff
OA OA
La focale de la lentille équivalente doit être égale à d0 (vision à l'infini sans accommodation) lorsque f ’0 = f ’:
10
1
''
'''
eq ff
fff
; f ’1 = d0f ’ / (f ’ – d0 ) la focale est f ’1 = d0f ’ / (f ’ – d0 ) = 153,3 mm et la vergence V = 6,52 
Cette lentille équivalente a également une focale variable :
' ' '
1 0 0 0
' ' '
1 0 0 0 0
'
'''
eq f f f f d
ff f d f f f d
On obtient donc pour les valeurs maximale et minimale de f ’0 : f ’eq,max = 20,75mm , f ’eq,min = 19,24mm
Le “punctum proximum” est donné par :
0 ,min
1 1 1
''eq df
OA
d'où la nouvelle valeur dm = 506 mm.
2.3. presbytie : On ne connaît plus la focale nominale de ( L0 ), on ne peut plus utiliser l'approche précédente. Ce
que nous connaissons sur (L0) est le “punctum proximum” supposé égal à 1m. D'un objet placé à 25 cm de O la
lentille (L1) doit former une image à 1 m en avant de O. Cette image sera certainement virtuelle. Ecrivons pour
cette dernière lentille la relation de conjugaison :
'
1
1 1 1 1 1
1000 250
'f OA OA
d'où : la focale est f’1 = 333,3
mm et la vergence V = 3 