Chapitre 1 - Diabolomaths
publicité
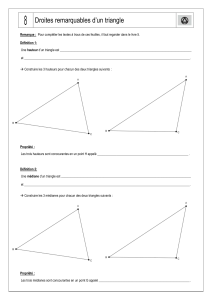
2 Triangles Droites remarquables du triangle Médiatrice Hauteur [G2] Mettre en œuvre ou écrire un protocole de construction d’une figure géométrique. Coder une figure. Résoudre des problèmes de géométrie plane, prouver un résultat général, valider ou réfuter une conjecture. • Triangle : inégalité triangulaire, cas d’égalité des triangles, hauteurs. • Médiatrice d'un segment. 3 semaines Construction de triangles et inégalité triangulaire. Triangles isométriques Médiatrice d’un segment (rappel de 6ème) Hauteurs d’un triangle. Reproduire un angle, maîtriser l'utilisation d'un rapporteur. Connaître et utiliser l’inégalité triangulaire. Construire un triangle connaissant : - les longueurs des trois côtés. - les longueurs de deux côtés et l’angle compris entre ces deux côtés. - la longueur d’un côté et les deux angles qui lui sont adjacents. Connaître et utiliser la définition de la médiatrice d’un segment ainsi que la caractérisation de ses points par la propriété d'équidistance. Utiliser différentes méthodes pour tracer la médiatrice d'un segment. Connaître et utiliser la définition d’une hauteur d’un triangle. S1 Les triangles Activité : Prendre 3 objets de la trousse (stylo – cartouches d’encre,…) et essayer de construire un triangle avec ces 3 objets en faisant en sorte que les extrémités se touchent. Question : Est-ce possible à chaque fois ? I. Inégalités triangulaires Dans tous les triangles, la mesure d’un côté est inférieure à la somme des 2 autres. A Exemple : AB < AC + BC AC < CB + BA BC < AB + AC B C Remarque : Pour vérifier si un triangle existe, il suffit de regarder le plus grand côté et les 2 plus petits C Remarque : BC = AB + AC A B On est dans le cas où A BC Exercices : 1 et 2 (fiche) + exercices 20 à 24 p 169 © Julien Fonteniaud Professeur de mathématiques S2 II. Constructions de triangles Insister sur le fait de vérifier si les triangles sont constructibles ou non Fiche : Lecture de la 1ère méthode Construction de type 1 (connaissant les 3 côtés) Exemple : A A 3 cm 2 cm B C B 4 cm C Avec les instruments A main levée Exercices : 3 (fiche) correction par calques S3 Fiche : Lecture de la 2ème méthode Construction de type 2 (connaissant 2 côtés et un angle) Exemple : E E 3 cm 30° F 4 cm D D F Avec les instruments A main levée Exercices : 4 et 5 (fiche) calques et calques S4 Fiche : Lecture de la 3ème méthode Construction de type 3 (connaissant 1 côté et 2 angles) Exemple : K I 45° 60° J I 4 cm A main levée © Julien Fonteniaud J K Avec les instruments Professeur de mathématiques Exercices : 6 et 7 (fiche) S5 Activité : placer 2 points au tableau A et B. Trouver les points à la même distance de A et de B. 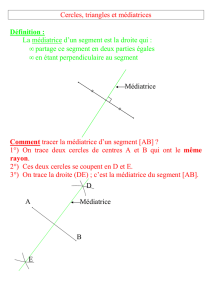III. Médiatrice d’un segment Définition : La médiatrice d’un segment [AB] est la droite (d) perpendiculaire à (AB), passant par le milieu de [AB]. B Tracé : I A Propriété 1 : Si M (d) , la médiatrice de [AB], alors MA = MB. Propriété 2 : Si M est un point équidistant de A et de B alors M (d) Remarque : Chaque triangle ABC possède un cercle passant par ses 3 sommets, appelé cercle circonscrit au triangle ABC. Le centre du cercle est le point d’intersection des médiatrices des 3 côtés du triangle. Exemple : C O A B © Julien Fonteniaud Professeur de mathématiques Exercices : Exercices 26 – 27 – 29 p 169 S6 Observer la figure – reconnaître et donner une définition de la hauteur IV. Hauteur Définition : Une hauteur, dans un triangle est une droite passant par un sommet perpendiculaire au côté opposé Exemple : Tracer la hauteur issue de A (ou relative à [BC]) dans chaque triangle : A A C B C B Exercices : 9 – 10 – 12 p 167 – 13 – 14 – 15 p 168 © Julien Fonteniaud Professeur de mathématiques
