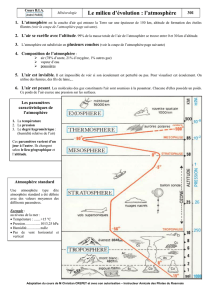
Conduction électrique 4 - Enseignement des Sciences Physiques

Conduction électrique : Résistance de l’atmosphère
Modèle très simplifié :
La Terre est supposé parfaitement sphérique (rayon R
T
).
L’état électrique de l’atmosphère par beau temps peut être décrit ainsi : le sol est à un potentiel V
1
négatif (on notera R
1
= R
T
), tandis que l’ionosphère est à un potentiel V
2
positif (sphère de rayon R
2
).
L’atmosphère constitue le milieu faiblement conducteur de conductivité électrique σ, compris entre R
1
et
R
2
.
Calculer la résistance de l’atmosphère ainsi modélisée en fonction de σ, R
1
et R
2
. On réalisera le
schéma correspondant à la modélisation.
Modèle plus élaboré :
En fait, la conductivité varie avec l’altitude. Pour en tenir compte, nous allons désormais
faire une étude locale, et considérer l’atmosphère comme le milieu contenu entre les armatures d’un
condensateur plan : d’une part le sol au potentiel V
0
, d’autre part un plan à l’altitude H symbolisant
l’ionosphère au potentiel V
H
(> V
0
).
On raisonne sur une surface S.
Un courant d’intensité I
0
traverse verticalement l’atmosphère. Le
courant de retour est assuré par les orages dont il ne sera pas
question.
La conductivité électrique varie avec l’altitude selon : σ = σ
0
.e
z/a
.
1. Définir le vecteur densité de courant en un point M de l’atmosphère en fonction de I
0
et S.
2. Exprimer le champ électrique en fonction de l’altitude z.
3. Au niveau du sol, on mesure le champ électrique  = E
0
. ; on trouve E
0
= - 100 V/m.
Calculer σ
0
.
4. Calculer la différence de potentiel entre le sol et le point d’altitude z = 1,80 m.
Pourquoi un individu n’est-il pas électrisé ?
5. Calculer la différence de potentiel V
0
– V
H
puis en déduire la résistance R de l’atmosphère.
Données : H = 50 km ; S = 5,09.10
14
m² ; I
0
= - 1 500 A ; a = 4 km
S z
V
H
V
0
H