Chapitre 2 : Champs.

Cours 1S
Chapitre 2 : Champs.
1. Notion de champs, définitions.
è Historique
• C’est en 1820 que le physicien danois Oersted met en évidence
qu’un fil métallique en cuivre parcouru par un courant électrique
génère un phénomène magnétique : une aiguille aimantée est
déviée. Il remarque, en déplaçant l’aiguille, que le phénomène est
spatial. Ses travaux, repris rapidement par Ampère aboutiront à
l’existence du courant électrique et à la convention de sens encore
utilisée aujourd’hui.
• Vers 1850, Faraday reprend des expériences
similaires en réalisant des spectres magnétiques
d’aimants. Il remarque que le « magnétisme »
diminue quand on s’éloigne de l’aimant et il fait le
lien entre magnétisme et électricité. C’est le début
de l’électromagnétisme.
• C’est en 1864 que Maxwell introduit la théorie
des champs.
è Définitions
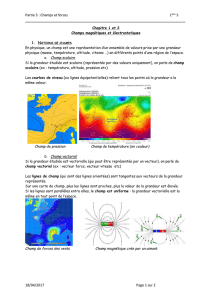
• Un champ est la représentation d’un ensemble de valeurs prises par une
grandeur physique en différents points d’une région de l’espace.
• Si la grandeur mesurée est un nombre, le champ est dit scalaire.
• Si la grandeur mesurée est un vecteur (3 informations sont nécessaires : direction,
sens et valeur), le champ est vectoriel.
• La carte d’un champ fait figurer les valeurs de la grandeur physique dans le cas
d’un champ scalaire et les vecteurs dans le cas d’un champ vectoriel.
• Dans le cas d’un champ vectoriel, la ligne tangente en chacun de ses points au
vecteur champ est appelée ligne de champ.
• Une équipotentielle (ou courbe de niveau) est la ligne obtenue en reliant tous
les points où la grandeur étudiée a la même valeur.
• Un champ vectoriel est dit uniforme si le vecteur champ qui le caractérise ne
dépend pas du point considéré : les caractéristiques du vecteur sont les mêmes.
Les lignes de champ sont alors des droites parallèles entre elles et la valeur du
champ est constante dans l’espace considéré.
2. Champ magnétique.
è Généralités
• Les aimants, les courants électriques, la Terre sont des sources
de champs magnétiques.
• Le champ magnétique 𝑩 est un champ vectoriel dirigé selon le
sens Sud-Nord d’une aiguille aimantée.
• L’intensité d’un champ magnétique se mesure avec un
teslamètre et s’exprime en Tesla (T)
è Lignes de champs
http://www.sciences.univ-nantes.fr/sites/genevieve_tulloue/Elec/Champs/topoB.html
Aimant droit
Fil parcouru par un courant
Spire
è Champ magnétique terrestre
• La Terre peut être considérée comme un aimant
droit.
• Le champ magnétique est dû aux mouvements de
matière dans le noyau de notre planète.
• L’ordre de grandeur de la valeur du champ
magnétique terrestre est 10-5 T.
3. Champ électrostatique.
è Charge et champ
http://www.sciences.univ-nantes.fr/sites/genevieve_tulloue/Elec/Champs/champE.html
• Un corps chargé électriquement crée autour de lui un champ
électrique, noté 𝑬.
Les lignes de champ sont orientées en fonction de la chargesource : si elle est positive, les lignes de champ partent de la
charge ; sinon, elles se dirigent vers la source.
• On détecte un champ électrostatique à l’aide
d’une charge q, elle subit une force 𝑭 = 𝒒×𝑬.
𝐹 et 𝐸 ont même sens pour q>0 et sens
contraire pour q<0.
La valeur de E est donc donnée par la relation : 𝑬 =
𝑭
𝒒
, exprimée en N.C-1.
è Cas d’un condensateur plan
• Un condensateur plan est formé de deux plaques
métalliques parallèles séparées par un isolant.
• Lorsqu’on applique une tension électrique U entre ces
deux plaques, le condensateur crée un champ électrostatique
𝐸 tel que : 𝐸 est uniforme et de direction perpendiculaire au
plan des plaques, dirigé de la plaque positive vers la plaque
négative et dont la valeur dépend de U et d, distance entre celles-ci.
𝑼
• On a : 𝑬 = 𝒅 , en V.m-1.
• Remarques : Les deux unités N.C-1 et V.m-1 sont équivalentes.
4. Champ de pesanteur.
• Au voisinage de la Terre, un objet de masse m est soumis à son poids 𝑷 tel que
𝑷 = 𝒎×𝒈.
• Le champ de pesanteur 𝑔 est dirigé selon la verticale du lieu et orienté vers le centre
𝑷
de la Terre. Sa valeur est donnée par = 𝒎 , exprimée en N.kg-1.
• En raison de la rotation de la Terre, le poids n’est pas exactement égal à la force
d’attraction gravitationnelle exercée par la Terre, mais la différence est faible. Au voisinage
𝑴
de la Terre, on peut considérer que 𝒈 = 𝑮× 𝑹𝟐𝑻
𝑻