Chapitre G3 Triangles et quadrilatères

Chapitre G3 Triangles et quadrilatères
I. Triangles
Définition :
Un triangle est un polygone à trois côtés.
Vocabulaire :
Un triangle a trois sommets et trois côtés.
Exemple : (voir manuel 1 p 134 : vidéo associée « triangles quelconques »)
Le triangle ABC a :
• trois sommets : les points A, B et C
• trois côtés : les segments [AB] ; [AC] et [BC]
• le sommet opposé au côté [AB] est C
• le côté opposé au sommet A est [BC]
Exemple : Construis un triangle VRM tel que VR = 5 cm ; RM = 7,5 cm et VM = 6 cm.
(voir manuel 1 p 134 : vidéo associée « constructions de triangles quelconques »)
Des triangles particuliers (voir manuel 2A p 134 : vidéo associée « triangles particuliers)
A. Triangle isocèle
Définition :
Un triangle isocèle est un triangle qui a deux côtés de la même longueur.
Vocabulaire :
• Le sommet commun aux deux côtés de même longueur est appelé le sommet principal.
• Le côté opposé au sommet principal est appelé la base.
Exemple : (voir manuel 2A p 134 : vidéo associée « constructions de triangles isocèles »)
Construire un triangle ISO isocèle en S tel que IO = 5 cm et IS = 4cm.
IS = SO = 4 cm
S est le sommet principal et
[IO] est la base du triangle ISO

B. Triangle équilatéral
Définition :
Un triangle équilatéral est un triangle qui a ses trois côtés de la même longueur.
Exemple :
Construire un triangle EQU équilatéral de côté 3 cm.
C. Triangle rectangle
Définition :
Un triangle rectangle est un triangle qui possède un angle droit.
Vocabulaire :
Le côté opposé à l'angle droit est appelé l'hypoténuse.
Exemple : Le triangle ABC est rectangle en B
^
ABC
est un angle droit
[AC] est l'hypoténuse
(voir manuel 2C p 135 : vidéo associée « constructions de triangles rectangles »)
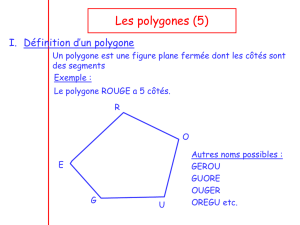
II. Quadrilatères
Définition :
Un quadrilatère est un polygone à quatre côtés.
Vocabulaire :
Un quadrilatère a quatre sommets ; quatre côtés et deux diagonales.
Exemple : (voir manuel 3 p 135 : vidéo associée « quadrilatères »)
Le quadrilatère EFGH a :
• quatre sommets : les points E, F, G et H.
• quatre côtés : les segments [EH] ; [EF] ; [GH] et [FG]
• deux diagonales : les segments [GE] et [FH].
• E et G sont des sommets opposés
• E et F sont des sommets consécutifs
• [GH] et [EF] sont des côtés opposés (pas de sommet en commun)
• [GH] et [GF] sont des côtés consécutifs (un sommet en commun)
Des quadrilatères particuliers
A. le trapèze
Définition :
Un trapèze est un quadrilatère qui a deux côtés opposés parallèles.
Exemple :
TRAP est un trapèze car (TR) // (PA)

B. le parallélogramme
Définition :
Un parallélogramme est un quadrilatère qui a ses côtés opposés parallèles deux à deux.
Exemple :
GRAM est un parallélogramme (GR) // (MA)
et (GM) // (RA)
C. le rectangle
Définition :
Un rectangle est un quadrilatère qui a ses quatre angles droits.
Exemples :
a) Construis un rectangle CHOU tel que CH = 6,5 cm et HO = 5 cm.
b) Construis un rectangle VERT tel que VE = 4 cm et VR = 5 cm.
D. le losange
Définition :
Un losange est un quadrilatère qui a ses quatre côtés de la même longueur.
Exemple :
Construis un losange ABCD tel que AB = 6 cm et BD = 4,2 cm.
ABD et BDC sont des
triangles isocèles
E. le carré
Définition :
Un carré est un quadrilatère qui a ses quatre côtés de la même longueur et ses quatre angles droits.
Remarque :
Un carré est à la fois un losange et un rectangle.
Exemple :
Construis un carré ILES de 3 cm de côté.