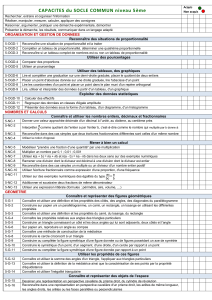
Agrandissement-Réduction d`une figure

Agrandissement-Réduction
d’une figure
Un Parcours d'Étude et de Recherche
à partir de la quatrième
Groupe didactique de l'Irem de Bordeaux
Nous publions ici une version courte de cet article du groupe didactique de
Bordeaux. La version complète est à lire sur le site de l'APMEP parmi les
compléments en ligne de ce bulletin.
0?,=?4.701,4?>@4?0F7,;=H>09?,?4:9/0.0$&$,=.:@=>/E?@/00?/0&0.30=.30
7:=> /@9 ,?0740= /0> 5:@=9H0> 8,?3H8,?4<@0> /0 7E 9>?4?@? =,9G,4> /0
7E/@.,?4:9 ,@ 8:4> /0 5@49  7 >49>.=4? /,9> @9 ;,=.:@=> ;7@> 7,=20 >@= 7,
;=:;:=?4:99,74?H 09 2H:8H?=40 ,@ .:77I20 <@4 10=, 7:-50? /0 7, ;@-74.,?4:9 /@90
-=:.3@=0=H/42H0;,=70=:@;0/4/,.?4<@0/07=08/0:=/0,@B
, 9:?4:9 /,2=,9/4>>0809?=H/@.?4:9 9U0>? ;,> AH=4?,-70809? @90 9:?4:9
8,?3H8,?4<@0770,H?H.=HH0;:@=HA4?0=/0;,=70=/3:8:?3H?40:@/0>48474?@/0
0??09:?4:99U0>?;,>?:@5:@=>/H14940/01,G:9?=I>=42:@=0@>0/,9>70>8,9@07>/0
.:77I200=?,490>=H/,.?4:9><@4C>:9?@?474>H0>;0@A09?7,4>>0=;09>0=<@U47>@114?/0
8@7?4;740= 70> .L?H> /U@90 142@=0 ;,= @9 8J80 9:8-=0 ;:@= 09 :-?094= @9
,2=,9/4>>0809?
!,4>471,@?1,4=0,??09?4:9S090110?;:@=,2=,9/4=@9.,==H:@@9=0.?,927047>@114?
/08@7?4;740=7,80>@=0/0>/0@B.L?H>;,=@90.:9>?,9?0?:@?09.:9>0=A,9?7,9,?@=0
/0> 142@=0> ,7:=> <@0 ;:@= @9 7:>,920 ;,= 0B08;70 .07, 90 >@114? ;,> $:@= @9
?=4,9270>:4?:98@7?4;7407,7:92@0@=/U@9>0@7.L?H0?:9.:9>0=A0/0@B,9270>>:4?
:98@7?4;7407,7:92@0@=/0/0@B.L?H>0?:9.:9>0=A07U,9270.:8;=4>09?=070>/0@B
>:4?:98@7?4;7407,7:92@0@=/0>?=:4>.L?H>;,=708J801,.?0@=
01,G:92H9H=,70;:@=,2=,9/4=:@=H/@4=0@90142@=0471,@?.3:4>4=70>H7H809?>
<@4>@114>09?;:@==0;=:/@4=07,142@=0F@904>:8H?=40;=I>7:92@0@=>:@,9270>
;@4>8@7?4;740=70>7:92@0@=>,49>4>H70.?4:99H0>;,=@91,.?0@=.:9>?,9?0?.:9>0=A0=
70>,9270>.3:4>4>
9?@4?4A0809?;:@=70>H7IA0><@,9/:9,2=,9/4?:9,5:@?0<@07<@0.3:>0<@,9/:9
,2=,9/4?>,8,4>:9:9,5:@?0@90;4I.0S<@,9/:9=H/@4?:9097IA0<@07<@0.3:>0
0>?/:9.@9;:49?48;:=?,9?<@47901,@?;,>;,>>0=>:@>>4709.0
":@>;=:;:>:9>@909.3,K90809?/0>4?@,?4:9>;:@=?=,4?0=70?3I80,2=,9/4>>0809?
=H/@.?4:9,@.:77I20<@09:@>,;;07:9>PS;,=.:@=>SQ09=H1H=09.0,@B$&$,=.:@=>
Dossier : Collège 2 55
APMEP
no512
IREM de Bordeaux-Taxte_Mise en page 1 19/01/15 12:46 Page55

/UE?@/0 0? /0 &0.30=.30 ?3H:=4>H> ;,= +A0> 30A,77,=/ 0 ?=,A,47 /0 7U&!
/U<@4?,490>U49>.=4?/,9>70.,/=0/07,=0.30=.30$&!'$,=.:@=>/UE?@/00?/0
&0.30=.30 09 !,?3H8,?4<@0> ;:@= 79>04290809? '0.:9/,4=0 09 .:77,-:=,?4:9
09?=07U&!0?7UE49>?4?@?=,9G,4>/07E/@.,?4:90B"&$
)90=,4>:9/J?=0/0.0;,=.:@=>S70;=:2=,880/0<@,?=4I80=H/@4?70?3H:=I80/0
(3,7I>,@?=4,92700?70=0740,@.:9.0;?/,2=,9/4>>0809?=H/@.?4:9/0?=4,9270>
0 ;,=.:@=> <@0 9:@> ;=:;:>:9> 09 .7,>>0 /0 <@,?=4I80 ;0=80? /,-:=/ /0 1,4=0
H80=20= 7, ;=:;:=?4:99,74?H 0? 7, .:9>0=A,?4:9 /0> ,9270> /0 .:9>4/H=0= 70>
,2=,9/4>>0809?>=H/@.?4:9>/0142@=0>092H9H=,7;:@=,-:@?4=,@.,>;,=?4.@740=/0>
?=4,9270>0?F7,;=:;=4H?H/0(3,7I>PA0=>4:9<@,?=4I80Q,9>@9/0@B4I80?08;>
47;0=80?/494?40=7,1:=80P.7,>>4<@0Q/@?3H:=I80,A0.7H2,74?H/0>=,;;:=?>;@4>
7,.,=,.?H=4>,?4:92=,;34<@0/07,;=:;:=?4:99,74?H
0>,.?4A4?H>/H?@/00?/0=0.30=.30&<@4.:9>?4?@09?.0;,=.:@=>@?474>09?@9
8,?H=407 .:9.=0? >48;70 ;=H>09? /,9> 7, .7,>>0 <@0 70> H7IA0> ;0@A09? 8,94;@70=
;3:?:> ?=4,9270> 0? =0.?,9270> F /H.:@;0= R , 8:/H74>,?4:9 9H.0>>,4=0 ;:@=
1,4=0,;;,=,K?=00?.:8;=09/=070=L70/0>8,?3H8,?4<@0>0>??=I>>48;70
0>H7IA0>@?474>0=:9?4.470>:@?47>3,-4?@07>/07,;=:;:=?4:99,74?HS>.3H8,17H.3H
?,-70,@R,A0.@?474>,?4:9/0>.:0114.409?>/0;=:;:=?4:99,74?H/07,;=:;=4H?H/0
749H,=4?H ,;=:2=0>>4:9;=:;:>H0,8I9070>H7IA0>F/H.:@A=4=0?80??=009;7,.0
/,@?=0>:@?47>SH2,74?H/0=,;;:=?>2=,;34<@01:=8@70 ,;=:;:=?4:99,74?H=0/0A409?
/:9.:-50?/H?@/0,A0.>,.,=,.?H=4>,?4:92=,;34<@0H?@/0<@4>0?0=8490=,;:@=70
.:77I20;,=7,1:9.?4:9749H,4=0
0;,=.:@=>>49>.=4?/:9.;,=1,4?0809?09<@,?=4I80/,9>70?=,A,47F8090=>@=7,
;=:;:=?4:99,74?H0?;0=80?,@>>4/0/:990=/@>09>F749?=:/@.?4:9/07,9:?4:9/0
.:>49@>;,=0B08;70":@>9U,A:9>;,>49.7@>7U&>@=70.:>49@>/,9>.0?,=?4.70
8,4>0770>U,=?4.@70;,=1,4?0809?,A0..0<@40>?;=:;:>H4.4
;=I>,A:4=-=4IA0809?=,;;07H70>,??09/@>/@;=:2=,880:114.4079:@>0B;:>0=:9>
/,9> @90 ;=084I=0 ;,=?40 @9 09.3,K90809? /0 ?=:4> >4?@,?4:9> >@= 70 ?3I80 /0
7,2=,9/4>>0809?/@90;3:?:/,9>@90/0@B4I80;,=?40?=:4>>4?@,?4:9>,809,9?7,
;=:;=4H?H/0(3,7I>/,9>>,PA0=>4:9<@,?=4I80Q,9>@90?=:4>4I800?/0=94I=0
;,=?40 0? 09 2@4>0 /0 .:9.7@>4:9 9:@> ;=:;:>0=:9> 7, ;=:2=0>>4:9 .:9>?4?@,9? 70
;,=.:@=> ,99:9.H 8:9?=,9? 748-=4.,?4:9 /0 .0> /411H=09?0> >4?@,?4:9> 09?=0 0770>
,49>4<@0<@07<@0>,.?4A4?H>.:8;7H809?,4=0>8,4>0>>09?40770>;:@=7,.:3H=09.0/@
;,=.:@=>
7,>>0/0<@,?=4I80
)?474>,?4:9/07,;=:;:=?4:99,74?H
H?0=8490=@90<@,?=4I80;=:;:=?4:990770
@B/4A0=>0>;=:.H/@=0>/H5FH?@/4H0>>U,5:@?070P;=:/@4?09.=:4BQ<@4/:4?J?=0
5@>?414H
56 Dossier : Collège 2 APMEP
no512
*:@>;:@A0D?=:@A0=7,>4?@,?4:9>@=7U49?=:/@.?4:9/@.:>49@>09<@,?=4I80/,9>$0?4?B
9N
IREM de Bordeaux-Taxte_Mise en page 1 19/01/15 12:46 Page56

$=:;:=?4:99,74?H
T)?474>0=/,9>70;7,98@94/U@9=0;I=07,.,=,.?H=4>,?4:9/07,;=:;:=?4:99,74?H
42@=0>;7,90>
(=4,927084740@B0?;,=,77I70>
T:99,K?=00?@?474>0=70>?3H:=I80>=07,?41>,@B84740@B/0/0@B.L?H>/U@9?=4,9270
,9>70.,/=0/@>:.70.:88@9>0@70>70>;=:;=4H?H>/4=0.?0>/07,/=:4?0/0>84740@B
>:9?0B424-70>
TConnaître et utiliser la proportionnalité des longueurs pour les côtés des deux
triangles déterminés par deux parallèles coupant deux demi-droites de même
origine.
0?3H:=I80/0(3,7I>/,9>?:@?0 >,2H9H=,74?H0?>,=H.4;=:<@0 >0=:9?H?@/4H>09
.7,>>0/0?=:4>4I80
2=,9/4>>0809?=H/@.?4:9
T 2=,9/4= :@ =H/@4=0 @90 142@=0 09 @?474>,9? 7, .:9>0=A,?4:9 /0> ,9270> 0? 7,
;=:;:=?4:99,74?H09?=070>7:92@0@=>/07,142@=0494?4,700?/0.0770>/07,142@=0F
:-?094=
0> ,.?4A4?H> /0 .:9>?=@.?4:9 ,A0. HA09?@0770809? 7U@?474>,?4:9 /0 7:24.407> /0
.:9>?=@.?4:92H:8H?=4<@0;0=80??09?,@BH7IA0>/080??=009HA4/09.00?/U@?474>0=
<@07<@0>;=:;=4H?H>.:9>0=A,?4:9/0>,9270>0?/:9./07,;0=;09/4.@7,=4?H0?/@
;,=,77H74>808@7?4;74.,?4:9/0>7:92@0@=>;,=701,.?0@=6/U,2=,9/4>>0809?:@/0
=H/@.?4:9R
0=?,49>;=:.H/H>/0.:9>?=@.?4:9;0@A09?J?=0,9,7C>H>09@?474>,9?70?3H:=I80/0
(3,7I>/,9>70?=4,9270
7,>>0/0?=:4>4I80
:9142@=,?4:9/0(3,7I>
T Connaître et utiliser la proportionnalité des longueurs pour les côtés des deux
triangles déterminés par deux parallèles coupant deux droites sécantes.
TConnaître et utiliser un énoncé réciproque
7 >U,24? /0 ;=:7:920= 7UH?@/0 .:8809.H0 09 .7,>>0 /0 <@,?=4I80 <@4 >0@70 0>?
0B424-70/,9>70.,/=0/@>:.70.:88@9
0>:-50.?41>A4>H>4.4;,=.0?09.3,K90809?/0?=:4>>4?@,?4:9>>:9?S
O /@90 ;,=? /0 =0;=09/=0 7U,;;=09?4>>,20 /0 7, ;=:;:=?4:99,74?H ,@?=0809?
<@U09?0=80>/0=HA4>4:909;,=?,9?/@.,/=02H:8H?=4<@00?09,77,9?A0=>70
.,/=02=,;34<@0/:9./411H=08809?/0>;=:-7I80>,=4?38H?4<@0><@4>0=A09?
092H9H=,7F0B0=.0=70>H7IA0>>@=7,;=:;:=?4:99,74?H/0;@4>70.:@=>8:C09S
O /,@?=0 ;,=? /0 1,4=0 @9 ;=0840= ;,> A0=> 7, 1:9.?4:9 749H,4=0 0? >,
=0;=H>09?,?4:92=,;34<@0090B;74<@,9?7U,74290809?/0>;:49?>0?8J807,
9:?4:9/0;09?0/@90/=:4?0S
Agrandissement d'une photo, situation 1: «partie intuitive»
,.:9>4290
(=:4>>H=40>/0;3:?:>>:9?;=:;:>H0>09A4/H:;=:50.?4:9,@BH7IA0>
Agrandissement-réduction d’une figure 57
APMEP
no512
IREM de Bordeaux-Taxte_Mise en page 1 19/01/15 12:46 Page57

770@=0>?>48;70809?/08,9/H/:->0=A0=.0>;3:?:>;:@=;:@A:4=09>@4?01,4=0/0>
.:8809?,4=0>0?/0>=08,=<@0>:=,70809?
$=084I=0>H=40S
0@B4I80>H=40S
(=:4>4I80>H=40S
,9>7,/4>.@>>4:909.7,>>009?4I=070>H7IA0>@?474>09?70>8:?>PS,;7,?4H?4=H?=:;
849.0 ;7@> 7,=20 /H1:=8H ,2=,9/4 ;,=047 09 7:92@0@= 0? 09 7,=20@= RS Q 0.4
;0=80?/0>080??=0/U,..:=/>@=701,4?<@0>4@90;3:?:0>?.:==0.?0809?,2=,9/40
?:@>70>H7H809?>/07U48,20>:9?,2=,9/4>PS/07,8J801,G:9SQ.:880/,9>@90
8,<@0??0 :@ F 7U49A0=>0 ?:@> 70> H7H809?> /0 7U:-50? >:9? =H/@4?> PS /0 7, 8J80
1,G:9SQ
(:@?0>70>/4809>4:9>/07,;3:?:/:4A09?J?=0,2=,9/40>/07,8J801,G:9,149<@0
70>48,20>90>:409?;,>/H1:=8H0>,9>@9;=0840=?08;>70;=:10>>0@=;0@?>0
.:9?09?0=/0.0??01:=8@7,?4:9;:@=.,=,.?H=4>0=.0??0?=,9>1:=8,?4:9S47>U,24?/U@90
>48474?@/08,4>.08:?9U0>?;,>49?=:/@4? 0;=:2=,880;,=70/U,2=,9/4>>0809?0?
58 Dossier : Collège 2 APMEP
no512
IREM de Bordeaux-Taxte_Mise en page 1 19/01/15 12:46 Page58

/0=H/@.?4:9 08:?PS,2=,9/4>>0809?SQ0>?,8-42@S>45U,2=,9/4>8,8,4>:950
=,5:@?0@90;4I.050901,4>;,>@903:8:?3H?4094@90>48474?@/0R 0=0.:@=>F7,
;3:?: ;0=80? ,@ ;=:10>>0@= /0 >0 1,4=0 -409 .:8;=09/=0 >@= .0 <@U47 09?09/ ;,=
PS,2=,9/4>>0809?=H/@.?4:9SQ'4708:?;=:;:=?4:99,74?H0>?;=:9:9.H/,9>7,.7,>>0
70;=:10>>0@=;0@?70=0;=09/=0>49:9479070;=:9:9.0;,>
0>0@7:-50.?41/0.0??0;=084I=0>4?@,?4:90>?/:9./0PS14B0=SQ49?@4?4A0809?,A0.
7,.7,>>07,9:?4:9/,2=,9/4>>0809?=H/@.?4:9S7,.:9>0=A,?4:9/07,PS1:=80SQ7
90>?;,><@0>?4:94.4/09A4>,20=7,.:9>0=A,?4:9/0>,9270>.07,A409/=,;7@>?,=/
Agrandissement d'une photo, situation 2: la proportionnalité
,.:9>4290
PS#9.:9>4/I=0@90;3:?:<@40>?@9=0.?,9270/0S.8>@=S.8S50A0@B7U,2=,9/4=
/0>:=?0<@07,7:92@0@=<@40>?S.8/0A40990S.8
%@07700>?7,7,=20@=/07,9:@A0770;3:?:S
9/4<@0=70>.,7.@7>1,4?>0?/0>>490=70=0.?,9270=0;=H>09?,9?7,;3:?:,2=,9/40SQ
 ,/4809>4:9S.8;0@?;=J?0=F.:91@>4:9,A0.70.:0114.409?/0;=:;:=?4:99,74?H
09?=07,=20@=0?7:92@0@=/@=0.?,9270494?4,7#9;:@==,HA09?@0770809?;=09/=0@9
=0.?,9270/0S.8;,=S.80?/08,9/0=<@07,7,=20@=S.8/0A40990S.8
*:4.4/411H=09?0>=H;:9>0>:@;=:.H/@=0>/H7IA0><@4:9??=,A,477H>@=@90;3:?:/0
.8>@=.8
, PSU,5:@?0S.8;:@=:-?094=S.8/:9.5U,5:@?0S.8FS.8;:@=:-?094=7,
9:@A07707,=20@=0?5U:-?409>S.8SQ
- 0=?,49>;=:;:>09?SPSS-S=/:9.S-S=SQ
. PSH?,9?7,8:4?4H/0/:9.>47,9:@A07707:92@0@=0>?S.8:9/:4??=:@A0=
;:@=7,9:@A07707,=20@=7,8:4?4H/0S.8>:4?S.8SQ
/
S=¥S=70.:0114.409?/0;=:;:=?4:99,74?H0>? 
#@SS ,A0.7@?474>,?4:9/07H2,74?H/0>;=:/@4?>09.=:4B
0
S¥S=/:9.S¥S=
,9>.0.,>70.:0114.409?/0;=:;:=?4:99,74?H0>?
1 0=?,49>H7IA0>:9?-0>:49/0;,>>0=;,=7U@94?H7>;,=709?;,=1:4>/0=I270/0
?=:4>
7
4
7
4
72
4
×
Agrandissement-réduction d’une figure 59
APMEP
no512
IREM de Bordeaux-Taxte_Mise en page 1 19/01/15 12:46 Page59