Reconnaître les formes géométriques- le Tangram

___________________________________________________________________________________
__
Mathématiques Date de création : 10/2007
Géométrie Date d’actualisation :
La géométrie avec le tangram
Public : - Primaire et secondaire.
Durée : - ¼ d’heure à ½ heure.
Matériel : - Carton ou papier, ciseaux ou
tangram déjà réalisé.
Jeu de base (dans l’armoire
___________________________________________________________________________________
Objectif(s) : - Permettre aux enfants de s’approprier les formes géométriques en les manipulant.
- Evoquer les formes géométriques.
- S’approprier le vocabulaire de base en géométrie.
___________________________________________________________________________________
Déroulement de(s) activité(s) :
Présentation du jeu
Le tangram est un jeu d’origine chinoise dont le nom signifie « plaquette de sagesse » et il est très
populaire dans son pays d’origine. Les jeunes comme les moins jeunes l’utilise dans différentes
activités. Il peut servir de support pour illustrer des contes et des légendes, ou bien être un objet d’art
contemplatif.
Ici, nous l’utiliserons comme outil pédagogique.
Le tangram se compose de sept pièces : 5 triangles (2 grands, 1 moyen et deux petits), d’un carré et d’un
parallélogramme. Pour les plus jeunes il existe un jeu de 5 pièces.
Un aspect intéressant, qui est souvent oublié, est que le petit triangle représente l’unité de base du
tangram. Il peut reproduire l’ensemble des autres pièces (deux petits triangles forment le carré lorsqu’on
les rassemblent par hypoténuse, etc.).
C’est de cette particularité dont nous nous servirons dans les activités suivantes.

___________________________________________________________________________________
__
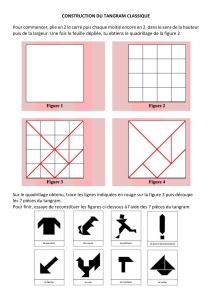
Première étape : reconnaître les formes et les caractériser.
Vous montrez aux enfants les pièces du tangram. Si possible, utiliser un gabarit pour le reproduire sur
du papier. Pièce après pièce, vous décrivez, en faisant participer les enfants, les caractéristiques de
chaque forme géométrique ; Cacher la pièce et laisser un temps aux enfants pour qu’ils la revoient dans
leur tête et se répètent les caractéristiques. L’intervenant fait un va et vient jusqu’à ce que la description
soit juste ; Ensuite, les enfants la dessinent et écrivent les caractéristiques.
Le triangle rectangle isocèle : Il a trois côtés, dont deux de même longueur.
Il a trois angles, un angle droit et deux angles aigus.
Il a un axe de symétrie (montrez par pliage).
Le carré : Il a quatre côtés de même longueur (quadrilatère).
Il a quatre angle droit.
Il a quatre axes de symétrie.
Le parallélogramme : Il a quatre côtés. Les côtés opposés sont de même longueur.
Il a quatre angles. Les angles opposé ont le même écartement.
Deux sont aigus, les deux autres sont obtus.
Il n’a pas d’axe de symétrie.
Ce travail est nécessaire à l’enfant pour qu’il s’approprie le vocabulaire propre à la géométrie.
L’intervenant peut à tout moment demander aux enfants de montrer où sont les angles droits, où sont les
angles aigus, les côtés, etc.
Quand l’enfant se trompe, toujours le questionner pour déterminer la cause de son erreur : Est-elle lié à
une mauvaise compréhension du vocabulaire ? Si c’est le cas, l’intervenant redonne la définition juste
du vocabulaire. Ainsi de suite jusqu’à ce que l’enfant intègre bien ces notions.
La manipulation tactile favorise l’apprentissage. Laissez les enfants manipuler autant qu’ils le
souhaitent les pièces du tangram. C’est une façon pour eux de s’approprier les formes géométriques,
beaucoup plus concrète que de regarder les formes géométriques sur un livre. Par exemple, l’angle aigus
pique quand je le mets au creux de ma main alors que l’angle obtus lui ne me pique pas, etc.

___________________________________________________________________________________
__
Deuxième étape : exercices pratiques
Une fois ce travail préalable fait avec les enfants, vous allez pouvoir passer à un exercice pratique
mettant en œuvre la recherche par tâtonnements pour en arriver à un raisonnement par déduction.
Munissez-vous des trois plus petits triangles (les deux petits et le moyen), du carré et du
parallélogramme.
A chaque enfant, chacun à son tour, vous lancerez un défi :
- Tiens je te donne les deux petits triangles. Avec ces deux petits triangles tu vas devoir me
reconstituer le carré.
Vous laissez à disposition de l’enfant le carré comme modèle. L’enfant va procéder par tâtonnement en
faisant pivoter les triangles jusqu’à ce qu’il arrive à reproduire le carré. Une fois qu’il arrive au résultat,
n’hésitez pas à le questionner pour savoir comment il a procédé ; A t-il revu dans sa tête les gestes que
vous aviez fait lorsque vous décriviez le carré ? A t-il simplement procédé par essai ?
L’objectif est bien sûr d’amener chaque enfant à utiliser une méthode déductive (par exemple, le carré
dispose d’axes de symétrie -diagonales- qui le divise en deux triangles rectangle isocèle, et donc si je
réunis deux triangles rectangles isocèles par leurs hypoténuses, j’obtiens alors un carré).
Les enfants dans l’étape décrite ci-dessus ont tendance à être très silencieux (ils se concentrent) mais
invitez les à formuler ce qu’ils ont dans la tête afin que vous puissiez les orienter dans la bonne voie,
sans pour autant leur donner la solution. Il est très important que l’enfant réussisse seul, sans que vous
lui donniez la réponse.
A chaque étape de cet exercice, vous devez formuler le maximum de règles mathématique possibles.
Par exemple dans le cas ci-dessus, la diagonale du carré est égale à la longueur de l’hypoténuse du
triangle, etc. L’intervenant peut noter toutes ces règles, mais le plus intéressant serait que se soit les
enfants qui inscrivent ces règles sur une feuille ou un cahier de brouillon. Quand l’exercice sera
terminé, un volontaire relira l’ensemble des règles découvertes grâce à l’activité.
Procédez ainsi de suite, en donnant à chaque enfant une figure différente et essayez, si le temps vous le
permet, de refaire suffisamment de tour de table pour que chaque enfant ait fait chacune des figures.
Cela est bénéfique pour chacun, car les enfants apprennent de leurs erreurs mais également des erreurs
de leurs petits camarades. N’oubliez pas que ce sont nos erreurs qui nous font progresser.