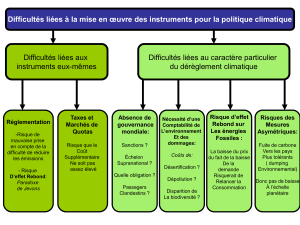
TD2 - STAPS

TD Biomécanique 2
- 1 -
Exercice 1
Le tableau suivant présente les records du monde du 100 m au 800 m en athlétisme
Record du monde Homme
100 m 9''78 Tim Montgomery (E-U) 14/09/2002
200 m 19''32 Michael Johnson (E-U) 01/08/1996
400 m 43''18 Michael Johnson (E-U) 26/08/1999
800 m 1'41''11 Wilson Kipketer (Dan) 24/08/1997
1. Pour chaque record calculer la vitesse moyenne en km/h
2. Déterminer l’écart en % sur les vitesses entre 100m et 200m, 200m et 400m et 200m et 800m
Exercice 2
Le tableau suivant présente l’évolution des temps de passage de trois athlètes lors de la finale
olympique du 100 m des jeux de Séoul.
Temps passage (s)
10 20 30 40 50 60 70 80 90 100
B. Johnson 1.83 2.87 3.8 4.66 5.5 6.33 7.17 8.02 8.89 9.79
C. Lewis 1.89 2.96 3.9 4.79 5.65 6.48 7.33 8.18 9.04 9.92
L. Christie 1.92 2.97 3.92 4.81 5.66 6.5 7.36 8.22 9.09 9.97
1. Déterminer pour chaque athlète l’évolution de sa vitesse (en km/h) au cours de sa course
2. Tracer sur un même graphe la vitesse des trois athlètes
3. Décrire ces courbes de vitesses
Exercice 3
La figure suivante représente le rebond d’une balle de tennis (de diamètre 7 cm et de masse 60g)
analysé par un système émettant des flashs toutes les 4 ms.
1. Déterminer l’échelle de la figure
2. Déterminer la vitesse moyenne de la balle avant et après le rebond
3. Déterminer les composantes horizontales et verticales de la vitesse de la balle avant et après le
rebond
4. Calculer l’énergie cinétique de la balle avant et après le rebond
y
x

TD Biomécanique 2
- 2 -
(S)
O
A
→
→
→
→
→
Exercice 4
Soit une barre articulée (S) de longueur l tournant autour de l’axe (O, z
0
), avec une vitesse
instantanée de rotation Ω
ΩΩ
Ω, on définit deux repères :
 Repère d’étude fixe R
0
(0, x
0
, y
0
, z
0
)
 Repère mobile attaché à (S) R
1
(A, x
1
, y
1
, z
0
)
1. Calculer la vitesse   ∈
→
du point A par rapport à R
0
en utilisant la formule de distribution
des vitesses dans (S)
2. Appliquer le résultat obtenu au calcul de la vitesse de rotation nécessaire pour lancer le disque
avec une vitesse de 20 m/s. On supposera que la rotation s’effectue autour du buste de l’athlète et
que son envergure est de 2.1 m.
Exercice 5
Soit R
0
(0, x
0
, y
0
, z
0
) un repère galiléen, on applique en O une force
→→
= .
1. Calculer le moment
→
→
de
→
2. Application numérique : F = 2000 N, l = 0.5 m et
θ
=0°, 5° et 30°
G
O
→
→
→
θ
0G = l

TD Biomécanique 2
- 3 -
Correction exercice 1
1. Pour calculer la vitesse moyenne, il convient de diviser la distance par le temps. La vitesse obtenue
est exprimée en m/s. Pour la convertir en km/h, il faut la multiplier par 3.6.
Distance (m) Temps (s) vitesse (m/s) vitesse (km/h)
100 9.78 10.22 36.81
200 19.32 10.35 37.27
400 43.18 9.26 33.35
800 101.11 7.91 28.48
vitesse (km/h)
25
27
29
31
33
35
37
39
100 200 400 800
2. Le calcul de la différence de vitesse s’effectue simplement :
 ×
−
=
différence (%)
200-100 1.24
400-200 -10.51
800-400 -14.59
800-200 -23.57
différence (%)
-25
-20
-15
-10
-5
0
5
200-100 400-200 800-400 800-200

TD Biomécanique 2
- 4 -
Correction exercice 2
1. Comme pour l’exercice 1, le calcul de la vitesse s’effectue sur chaque intervalle de 10 m en divisant
10 par le temps mis pour parcourir cet intervalle. Pour les 30m de la course de B. Johnson,
 =
−
= . On convertit ensuite ces vitesses en km/h en multipliant par 3.6.
Vitesse (km/h)
10 20 30 40 50 60 70 80 90 100
B. Johnson 19.67 34.62 38.71 41.86 42.86 43.37 42.86 42.35 41.38 40.00
C. Lewis 19.05 33.64 38.30 40.45 41.86 43.37 42.35 42.35 41.86 40.91
L. Christie 18.75 34.29 37.89 40.45 42.35 42.86 41.86 41.86 41.38 40.91
2.
15.00
20.00
25.00
30.00
35.00
40.00
45.00
10 20 30 40 50 60 70 80 90 100
B. Johnson
C. Lewis
L. Christie
3. On distingue 2 grandes zones :
- La première d’accélération jusqu’au 60m où la vitesse augmente de 19 à 42 km/h
- La seconde de stabilisation de la vitesse où l’athlète essaie de maintenir une vitesse
maximale supérieure à 40 km/h
On constate cependant que la vitesse diminue légèrement sur les vingt dernier mètres pour B.
Johnson alors que C. Lewis et L. Christie ont un meilleur finish.

TD Biomécanique 2
- 5 -
Correction exercice 3
1. Le diamètre mesuré sur le papier de la balle est de 1 cm contre 7 cm dans la réalité, le facteur
d’échelle de donc de 7
2. Pour calculer la norme de la vitesse moyenne avant puis après le rebond, nous allons utiliser 4
images soit 3 cycles.
 =
×
×
=
 =
×
×
=
3. Pour calculer les composantes de la vitesse, il faut projeter le vecteur vitesse sur les deux axes.
Avant le rebond
−=
×
×−
=
=
×
×
=
Après le rebond
=
×
×
=
=
×
×
=
y
x
6
2.4
5.5
3.2
1.6
2.8