Le cours - Académie de Nancy-Metz

Chapitre24 Parallélogrammes particuliers
1. Rectangles
1.1 Définition
Un rectangle est un quadrilatère qui a quatre angles droits.
Le quadrilatère ABCD a quatre angles
droits ; c'est un rectangle
1.2 rectangles et symétries
Un rectangle a un centre de symétrie : le point
d'intersection des diagonales.
Un rectangle a deux axes de symétrie : les médiatrices de
ses côtés.
Les droites (d1) et (d2) sont
les deux axes de symétrie du
rectangle EFGH.
Le point O est le centre de
symétrie du rectangle.
1.3 Propriétés
SI un quadrilatère est un rectangle ALORS :
●ses côtés opposés sont parallèles
●ses côtés opposés ont même longueur
●ses diagonales se coupent en leur milieu
●ses diagonales ont même longueur
●il a quatre angles droits
Remarque : Si un quadrilatère est un rectangle, ALORS c'est
aussi un parallélogramme.
Collège Jules Ferry Neuves Maisons doc a.garland p1

1.4 Reconnaitre un rectangle
1.4.1 Un quadrilatère particulier
SI un quadrilatère a ses diagonales de même longueur
et qui se coupent en leur milieu ALORS c'est un
rectangle.
SI un quadrilatère a trois angles droits ALORS c'est un
rectangle.
Collège Jules Ferry Neuves Maisons doc a.garland p2

1.4.2 Un parallélogramme particulier
SI un quadrilatère est un parallélogramme qui a ses
diagonales de même longueur ALORS c'est un
rectangle.
SI un quadrilatère est un parallélogramme qui a un
angle droit ALORS c'est un rectangle.
Collège Jules Ferry Neuves Maisons doc a.garland p3

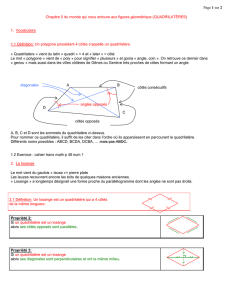
2. Losange
2.1 Définition
Un losange est un quadrilatère qui a ses quatre côtés de
même longueur.
Le quadrilatère ABCD a
quatre côtés de même
longueur : c'est un losange.
2.2 Losanges et symétries
Un losange a un centre de symétrie : le point d'intersection
des diagonales.
Un losange a deux
axes de symétrie : ses
deux diagonales.
2.3 Propriétés
SI un quadrilatère est un losange ALORS :
●ses côtés opposés sont parallèles
●ses quatre côtés ont même longueur
●ses diagonales se coupent en leur milieu
●ses diagonales sont perpendiculaires
●ses angles opposés ont même mesure
Remarque : Si un quadrilatère est un losange, ALORS c'est
aussi un parallélogramme.
Collège Jules Ferry Neuves Maisons doc a.garland p4

2.4 Reconnaitre un losange
2.4.1 Un quadrilatère particulier
SI un quadrilatère a quatre côtés de même longueur
ALORS c'est un losange.
SI un quadrilatère a ses diagonales perpendiculaires et
qui se coupent en leur milieu ALORS c'est un losange.
Collège Jules Ferry Neuves Maisons doc a.garland p5